Stiefel-Whitney class

A characteristic class with values in , defined for real vector bundles. The Stiefel–Whitney classes are denoted by , , and for a real vector bundle 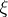over a topological space , the class lies in . These classes were introduced by E. Stiefel [1] and H. Whitney [2] and have the following properties. 1) For two real vector bundles over a common base,

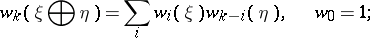in other words, , where is the complete Stiefel–Whitney class. 2) For the one-dimensional universal bundle over 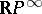the equality holds, where is the non-zero element of the group . These two properties together with naturality for induced bundles define the Stiefel–Whitney classes uniquely. The Stiefel–Whitney classes are stable, i.e. 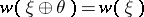, where 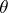is the trivial bundle, and for 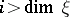. For an oriented -dimensional vector bundle 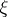over a base , 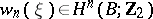coincides with the reduction modulo 2 of the Euler class.

For a vector bundle 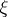over , let 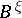be the Thom space of this bundle. Further, let be the Thom isomorphism. Then the complete Stiefel–Whitney class 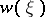coincides with

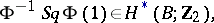where is the complete Steenrod square. This property of Stiefel–Whitney classes can be used as their definition. Stiefel–Whitney classes are homotopy invariants in the sense that they coincide for fibre-wise homotopically-equivalent bundles over a common base.

Any characteristic class with values in , defined for real vector bundles, can be expressed by Stiefel–Whitney classes: The rings 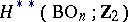and 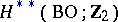are rings of formal power series in the Stiefel–Whitney classes:

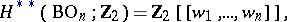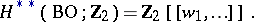References

[1]	E. Stiefel, "Richtungsfelden und Fernparallelismus in -dimensionalen Mannigfaltigkeiten" Comm. Math. Helv. , 8 : 4 (1935–1936) pp. 305–353
[2]	H. Whitney, "Topological properties of differentiable manifolds" Bull. Amer. Math. Soc. , 43 (1937) pp. 785–805
[3]	J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974)
[4]	R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968)
[5]	N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951)

Comments

The notation 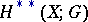denotes the product of the Abelian groups , while is the direct sum; the notation means that there is a graded homomorphism of degree : . For the classifying spaces and see Classifying space.

References

[a1]	D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)