Carnap rule
rule of infinite induction, $\omega$-rule
A derivation rule stating that if for an arithmetic formula $\phi(x)$ the propositions $\phi(0),\phi(1),\ldots,$ have been proved, then the proposition $\forall x\phi(x)$ can be regarded as being proved. This rule was first brought into consideration by R. Carnap [1]. Carnap's rule uses an infinite set of premises and is therefore inadmissible within the structure of the formal theories of D. Hilbert. The concept of a derivation in a system with the Carnap rule is undecidable. In mathematical logic one uses, for the study of formal arithmetic, the constructive Carnap rule: If there is an algorithm which for a natural number $n$ provides a derivation of the formula $\phi(n)$, then the proposition $\forall x\phi(x)$ can be regarded as being proved (the restricted $\omega$-rule, the rule of constructive infinite induction). Classical arithmetic calculus, which by Gödel's theorem is incomplete, becomes complete on adding the constructive Carnap rule (see [2], [3]).
References
| [1] | R. Carnap, "The logical syntax of language" , Kegan Paul, Trench & Truber (1937) (Translated from German) |
| [2] | A.V. Kuznetsov, Uspekhi Mat. Nauk , 12 : 4 (1957) pp. 218–219 |
| [3] | J.R. Shoenfield, "On a restricted 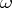 -rule" Bull. Acad. Polon. Sci. Cl. III , 7 (1959) pp. 405–407 -rule" Bull. Acad. Polon. Sci. Cl. III , 7 (1959) pp. 405–407 |
Carnap rule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carnap_rule&oldid=12356