D'Alembert operator

wave operator, d'Alembertian

The second-order differential operator which in Cartesian coordinates assumes the following form:

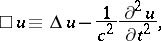where is the Laplace operator and is a constant. Its form in spherical coordinates is:

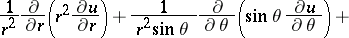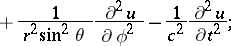in cylindrical coordinates:

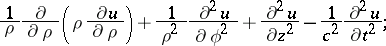in general curvilinear coordinates:

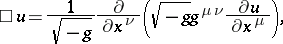where is the determinant of the matrix formed from the coefficients of the metric tensor .

Named after J. d'Alembert (1747), who considered its simplest form when solving the one-dimensional wave equation.

Comments

In the last equation above, the Einstein summation convention applies to the right-hand side (i.e. there is a summation involved over all ).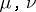

References

[a1]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German)
[a2]	F. John, "Partial differential equations" , Springer (1968)