Difference between revisions of "Nagel point"
From Encyclopedia of Mathematics
(Importing text file) |
(details) |
||
| Line 1: | Line 1: | ||
| − | The point of intersection of the straight lines joining the vertices of a triangle to the points at which the opposite sides are tangent to the escribed circles (see Fig.). | + | The point of intersection of the straight lines joining the vertices of a triangle to the points at which the opposite sides are tangent to the escribed circles (see Fig.). |
| + | |||
| + | This is named after Ch. Nagel (1836). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066010a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066010a.gif" /> | ||
| Line 6: | Line 8: | ||
| + | ====References==== | ||
| + | <table> | ||
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> N.A. Court, "College geometry" , Barnes & Noble (1952) pp. 160</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Berger, "Geometry" , '''I''' , Springer (1987) pp. Sect. 10.13.30</TD></TR> | ||
| + | </table> | ||
| − | + | {{OldImage}} | |
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 13:57, 8 April 2023
The point of intersection of the straight lines joining the vertices of a triangle to the points at which the opposite sides are tangent to the escribed circles (see Fig.).
This is named after Ch. Nagel (1836).
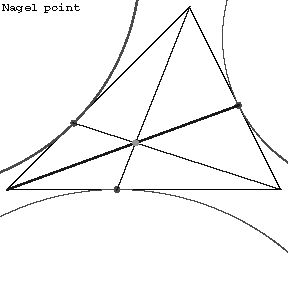
Figure: n066010a
References
| [a1] | N.A. Court, "College geometry" , Barnes & Noble (1952) pp. 160 |
| [a2] | M. Berger, "Geometry" , I , Springer (1987) pp. Sect. 10.13.30 |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Nagel point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nagel_point&oldid=53665
Nagel point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nagel_point&oldid=53665
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article