Difference between revisions of "Olevskii transform"
m (AUTOMATIC EDIT (latexlist): Replaced 15 formulas out of 17 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 17 formulas, 15 were replaced by TEX code.--> | Out of 17 formulas, 15 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
The [[Integral transform|integral transform]] | The [[Integral transform|integral transform]] | ||
Revision as of 17:47, 1 July 2020
\begin{equation} \tag{a1} F ( \tau ) = \end{equation}
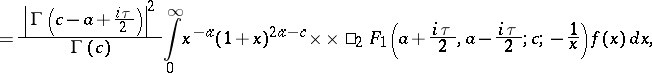 |
where $\square _ { 2 } F _ { 1 } ( a , b ; c ; z )$ is a Gauss hypergeometric function. It was introduced by M.N. Olevskii in [a1].
Letting $a = 1 / 2$, one obtains the Mehler–Fock transform. By changing the variable $x = \operatorname { sinh } ^ { - 2 } t$ and the respective parameters of the Gauss function, one obtains the Fourier–Jacobi transform [a2].
One can show that the Olevskii transform is the composition of the Kontorovich–Lebedev transform and the Hankel transform (cf. Integral transform; Hardy transform).
The Gauss function in the integral (a1) is the hypergeometric series for $x > 1$ and for $0 < x \leq 1$ one can understand it as an analytic continuation, which can be obtained from the Mellin–Barnes integral representation [a3].
The following integral transform is also called the Olevskii transform. It is an integral over the index $\tau$ of the Gauss function,
\begin{equation} \tag{a2} F ( x ) = \frac { x ^ { - a } ( 1 + x ) ^ { 2 a - c } } { \Gamma ( c ) } \times \end{equation}
\begin{equation*} \times \int _ { - \infty } ^ { \infty } \tau \left| \Gamma \left( c - a + \frac { i \tau } { 2 } \right) \right| ^ { 2 } \times \times \square _ { 2 } F _ { 1 } \left( a + \frac { i \tau } { 2 } , a - \frac { i \tau } { 2 } ; c ; - \frac { 1 } { x } \right) f ( \tau ) d \tau. \end{equation*}
Here, $f$ is an arbitrary odd function belonging to the space $L _ { 2 } ( \mathbf{R} ; \omega ( \tau ) )$, where
\begin{equation*} \omega ( \tau ) = \frac { \tau } { \operatorname { sinh } ( \pi \tau ) } \left| \frac { \Gamma ( c - a + \frac { i \tau } { 2 } ) } { \Gamma ( a + \frac { i \tau } { 2 } ) } \right| ^ { 2 } . \end{equation*}
The transform (a2) maps this space onto the space $L _ { 2 } ( \mathbf{R} _ { + } ; x ^ { - 1 } ( 1 + x ) ^ { c - 2 a } )$ and the Parseval equality holds:
\begin{equation*} \int _ { 0 } ^ { \infty } | F ( x ) | ^ { 2 } ( 1 + x ) ^ { c - 2 a } \frac { d x } { x } = \end{equation*}
\begin{equation*} = 8 \pi ^ { 2 } \int _ { - \infty } ^ { \infty } \tau \operatorname { sinh } ( \pi \tau ) \left| \frac { \Gamma ( c - a + \frac { i \tau } { 2 } ) } { \Gamma ( a + \frac { i \tau } { 2 } ) } | ^ { 2 } \right| f ( \tau ) | ^ { 2 } d \tau. \end{equation*}
References
| [a1] | M.N. Olevskii, "On the representation of an arbitrary function by integral with the kernel involving the hypergeometric function" Dokl. Akad. Nauk SSSR , 69 : 1 (1949) pp. 11–14 (In Russian) |
| [a2] | T.H. Koornwinder, "Jacobi functions and analysis on noncompact semisimple Lie groups" , Special Functions: Group Theoretical Aspects and Applications , Reidel (1984) pp. 1–85 |
| [a3] | S.B. Yakubovich, "Index transforms" , World Sci. (1996) pp. Chap. 7 |
Olevskii transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Olevskii_transform&oldid=50844