Difference between revisions of "Brauer second main theorem"
m (AUTOMATIC EDIT (latexlist): Replaced 54 formulas out of 56 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 56 formulas, 54 were replaced by TEX code.--> | Out of 56 formulas, 54 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
For notation and definitions, see [[Brauer first main theorem|Brauer first main theorem]]. | For notation and definitions, see [[Brauer first main theorem|Brauer first main theorem]]. | ||
Latest revision as of 17:43, 1 July 2020
For notation and definitions, see Brauer first main theorem.
Let $x$ be an element of $G$ whose order is a power of $p$. The $p$-section of $G$ associated to $x$ is the set of all elements of $G$ whose $p$-part is conjugate to $x$. Brauer second main theorem relates the values of irreducible characters of $G$ on the $p$-section associated to $x$ to values of characters in certain blocks of $C _ { G } ( x )$.
Suppose that 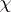 is an irreducible character of $G$ (cf. also Character of a group), afforded by the $R$-free right $R G$-module $V$, and belonging to the block $B$ (cf. also Defect group of a block). Let $x$ be a $p$-element of $G$, and let $H = C _ { G } ( x )$. For all $p$-subgroups $D$ of $H$, $C _ { G } ( D ) \subseteq H$; hence $b ^ { G }$ is defined for all blocks $b$ of $R H$. One can organize the block decomposition of $R H$ as $R H = ( \oplus _ { b ^{ G} = B } b ) \oplus (\oplus_{ b ^{ G} \neq B } b )$. Let $e$ be the projection of $1$ on $( \oplus _ { b ^G = B } b )$, and let $f$ be the projection of $1$ on $( \oplus _ { b ^{ G } \neq B } b )$. The restriction $V _ { H }$ of $V$ to $H$ can be decomposed as $V _ { H } = V _ { H } e \oplus V _ { H } f$. If $\chi _ { e }$ is the character of $V _ { H }e$ and $\chi _ { f }$ is the character of $V _ { H } f$, then of course $\chi ( h ) = \chi _ { e } ( h ) + \chi_{f }( h )$ for all $h \in H$. Brauer's second main theorem states that for all elements $y \in H$ of order prime to $p$, $\chi _ { f } ( x y ) = 0$. Thus, the values of
is an irreducible character of $G$ (cf. also Character of a group), afforded by the $R$-free right $R G$-module $V$, and belonging to the block $B$ (cf. also Defect group of a block). Let $x$ be a $p$-element of $G$, and let $H = C _ { G } ( x )$. For all $p$-subgroups $D$ of $H$, $C _ { G } ( D ) \subseteq H$; hence $b ^ { G }$ is defined for all blocks $b$ of $R H$. One can organize the block decomposition of $R H$ as $R H = ( \oplus _ { b ^{ G} = B } b ) \oplus (\oplus_{ b ^{ G} \neq B } b )$. Let $e$ be the projection of $1$ on $( \oplus _ { b ^G = B } b )$, and let $f$ be the projection of $1$ on $( \oplus _ { b ^{ G } \neq B } b )$. The restriction $V _ { H }$ of $V$ to $H$ can be decomposed as $V _ { H } = V _ { H } e \oplus V _ { H } f$. If $\chi _ { e }$ is the character of $V _ { H }e$ and $\chi _ { f }$ is the character of $V _ { H } f$, then of course $\chi ( h ) = \chi _ { e } ( h ) + \chi_{f }( h )$ for all $h \in H$. Brauer's second main theorem states that for all elements $y \in H$ of order prime to $p$, $\chi _ { f } ( x y ) = 0$. Thus, the values of 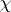 on the $p$-section associated to $x$ are determined in the blocks of $C _ { G } ( x )$ sent to $B$ by the Brauer correspondence (cf. also Brauer first main theorem).
on the $p$-section associated to $x$ are determined in the blocks of $C _ { G } ( x )$ sent to $B$ by the Brauer correspondence (cf. also Brauer first main theorem).
This theorem was first proved in [a1]. See also [a2], [a3], and [a4].
References
| [a1] | R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung II" Math. Z. , 72 (1959) pp. 22–46 |
| [a2] | C. Curtis, I. Reiner, "Methods of representation theory" , II , Wiley (1987) |
| [a3] | W. Feit, "The representation theory of finite groups" , North-Holland (1982) |
| [a4] | H. Nagao, Y. Tsushima, "Representation of finite groups" , Acad. Press (1987) |
Brauer second main theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brauer_second_main_theorem&oldid=50611