Difference between revisions of "Contiguity of probability measures"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 146 formulas out of 147 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 147 formulas, 146 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
The concept of contiguity was formally introduced and developed by L. Le Cam in [[#References|[a7]]]. It refers to sequences of probability measures, and is meant to be a measure of "closeness" or "nearness" of such sequences (cf. also [[Probability measure|Probability measure]]). It may also be viewed as a kind of uniform asymptotic mutual [[Absolute continuity|absolute continuity]] of probability measures. Actually, the need for the introduction of such a concept arose as early as 1955 or 1956, and it was at that time that Le Cam selected the name of "contiguity" , with the help of J.D. Esary (see [[#References|[a9]]], p. 29). | The concept of contiguity was formally introduced and developed by L. Le Cam in [[#References|[a7]]]. It refers to sequences of probability measures, and is meant to be a measure of "closeness" or "nearness" of such sequences (cf. also [[Probability measure|Probability measure]]). It may also be viewed as a kind of uniform asymptotic mutual [[Absolute continuity|absolute continuity]] of probability measures. Actually, the need for the introduction of such a concept arose as early as 1955 or 1956, and it was at that time that Le Cam selected the name of "contiguity" , with the help of J.D. Esary (see [[#References|[a9]]], p. 29). | ||
| − | There are several equivalent characterizations of contiguity, and the following may serve as its definition. Two sequences | + | There are several equivalent characterizations of contiguity, and the following may serve as its definition. Two sequences $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ are said to be contiguous if for any $A _ { n } \in\mathcal{ A} _ { n }$ for which $P _ { n } ( A _ { n } ) \rightarrow 0$, it also happens that $P _ { n } ^ { \prime } ( A _ { n } ) \rightarrow 0$, and vice versa, where $( {\cal X , A} _ { n } )$ is a sequence of measurable spaces and $P_n$ and $P _ { n } ^ { \prime }$ are measures on $\mathcal{A} _ { n }$. Here and in the sequel, all limits are taken as $n \rightarrow \infty$. It is worth mentioning at this point that contiguity is transitive: If $\{ P _ { n } \}$, $\{ P _ { n } ^ { \prime } \}$ are contiguous and $\{ P _ { n } ^ { \prime } \}$, $\{ P _ { n } ^ { \prime \prime } \}$ are contiguous, then so are $\{ P _ { n } \}$, $\{ P _ { n } ^ { \prime \prime } \}$. Contiguity simplifies many arguments in passing to the limit, and it plays a major role in the asymptotic theory of statistical inference (cf. also [[Statistical hypotheses, verification of|Statistical hypotheses, verification of]]). Thus, contiguity is used in parts of [[#References|[a8]]] as a tool of obtaining asymptotic results in an elegant manner; [[#References|[a9]]] is a more accessible general reference on contiguity and its usages. In a Markovian framework, contiguity, some related results and selected statistical applications are discussed in [[#References|[a11]]]. For illustrative purposes, [[#References|[a11]]] can be used as standard reference. |
| − | The definition of contiguity calls for its comparison with more familiar modes of "closeness" , such as that based on the | + | The definition of contiguity calls for its comparison with more familiar modes of "closeness" , such as that based on the $\operatorname {sup}$ (or $L_1$) norm, defined by |
| − | + | \begin{equation*} \| P _ { n } - P _ { n } ^ { \prime } \| = 2 \operatorname { sup } \{ | P _ { n } ( A ) - P _ { n } ^ { \prime } ( A ) | : A \in \mathcal{A} _ { n } \}, \end{equation*} | |
| − | and also the concept of mutual absolute continuity (cf. also [[Absolute continuity|Absolute continuity]]), | + | and also the concept of mutual absolute continuity (cf. also [[Absolute continuity|Absolute continuity]]), $P _ { n } \approx P _ { n } ^ { \prime }$. It is always true that convergence in the $L_1$-norm implies contiguity, but the converse is not true (see, e.g., [[#References|[a11]]], p. 12; the special case of Example 3.1(i)). So, contiguity is a weaker measure of "closeness" of two sequences of probability measures than that provided by sup-norm convergence. Also, by means of examples, it may be illustrated that it can happen that $P _ { n } \approx P _ { n } ^ { \prime }$ for all $n$ (i.e., $P _ { n } ( A ) = 0$ if and only if $P _ { n } ^ { \prime } ( A ) = 0$ for all $n$, $A \in {\cal A} _ { n }$) whereas $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ are not contiguous (see, e.g., [[#References|[a11]]], pp. 9–10; Example 2.2). That contiguity need not imply absolute continuity for any $n$ is again demonstrated by examples (see, e.g., [[#References|[a11]]], p. 9; Example 2.1 and Remark 2.3). This should not come as a surprise, since contiguity is interpreted as asymptotic absolute continuity rather than absolute continuity for any finite $n$. It is to be noted, however, that a pair of contiguous sequences of probability measures can always be replaced by another pair of contiguous sequences whose respective members are mutually absolutely continuous and lie arbitrarily close to the given ones in the sup-norm sense (see, e.g., [[#References|[a11]]], p. 25–26; Thm. 5.1). |
| − | The concept exactly opposite to contiguity is that of (asymptotic) entire separation. Thus, two sequences | + | The concept exactly opposite to contiguity is that of (asymptotic) entire separation. Thus, two sequences $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ are said to be (asymptotically) entirely separated if there exist $\{ m \} \subseteq \{ n \}$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120210/c12021035.png"/> such that $P _ { m } ( A _ { m } ) \rightarrow 0$ whereas $P _ { m } ^ { \prime } ( A _ { m } ) \rightarrow 1$ as $m \rightarrow \infty$ (see [[#References|[a2]]], p. 24). |
| − | Alternative characterizations of contiguity are provided in [[#References|[a11]]], Def. 2.1; Prop. 3.1; Prop. 6.1. In terms of sequences of random variables | + | Alternative characterizations of contiguity are provided in [[#References|[a11]]], Def. 2.1; Prop. 3.1; Prop. 6.1. In terms of sequences of random variables $\{ T _ { n } \}$, two sequences $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ are contiguous if $T _ { n } \rightarrow 0$ in $P_n$-probability implies $T _ { n } \rightarrow 0$ in $P _ { n } ^ { \prime }$-probability, and vice versa (cf. also [[Random variable|Random variable]]). Thus, under contiguity, convergence in probability of sequences of random variables under $P_n$ and $P _ { n } ^ { \prime }$ are equivalent and the limits are the same. Actually, contiguity of $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ is determined by the behaviour of the sequences of probability measures $\{ \mathcal{L} _ { n } \}$ and $\{ {\cal L} _ { n } ^ { \prime } \}$, where $\mathcal{L} _ { n } = \mathcal{L} ( \Lambda _ { n } | P _ { n } )$, $\mathcal{L} _ { n } ^ { \prime } = \mathcal{L} ( \Lambda _ { n } | P _ { n } ^ { \prime } )$ and $\Lambda _ { n } = \operatorname { log } ( d P _ { n } ^ { \prime } / d P _ { n } )$. As explained above, there is no loss in generality by supposing that $P_n$ and $P _ { n } ^ { \prime }$ are mutually absolutely continuous for all $n$, and thus the log-likelihood function $\Lambda _ { n }$ is well-defined with $P_n$-probability $1$ for all $n$. Then, e.g., $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ are contiguous if and only if $\{ \mathcal{L} _ { n } \}$ and $\{ {\cal L} _ { n } ^ { \prime } \}$ are relatively compact, or $\{ \mathcal{L} _ { n } \}$ is relatively compact and for every subsequence $\{ \mathcal{L} _ { m } \}$ converging weakly to a probability measure $\mathcal{L}$, one has $\int \operatorname { exp } \lambda d \mathcal{L} = 1$, where $\lambda$ is a dummy variable. It should be noted at this point that, under contiguity, the asymptotic distributions, under $P_n$ and $P _ { n } ^ { \prime }$, of the likelihood (or log-likelihood) ratios $d P _ { n } ^ { \prime } / d P_n$ are non-degenerate and distinct. Therefore, the statistical problem of choosing between $P_n$ and $P _ { n } ^ { \prime }$ is non-trivial for all sufficiently large $n$. |
| − | An important consequence of contiguity is the following. With | + | An important consequence of contiguity is the following. With $\Lambda _ { n }$ as above, let $T _ { n }$ be a $k$-dimensional random vector such that $\mathcal{L} [ ( \Lambda _ { n } , T _ { n } ) | P _ { n } ] \Rightarrow \tilde{\mathcal{L}}$, a probability measure (where "" stands for [[Weak convergence of probability measures|weak convergence of probability measures]]). Then $\mathcal{L} [ ( \Lambda _ { n } , T _ { n } ) | P _ { n } ^ { \prime } ] \Rightarrow \tilde{\mathcal{L}} ^ { \prime }$ and $\widetilde{ \cal L}'$ is determined by $d \tilde{L} ^ { \prime } / d \tilde{L} = \operatorname { exp } \lambda$. In particular, one may determine the asymptotic distribution of $\Lambda _ { n }$ under (the alternative hypothesis) $P _ { n } ^ { \prime }$ in terms of the asymptotic distribution of $\Lambda _ { n }$ under (the null hypothesis) $P_n$. Typically, $\mathcal{L} ( \Lambda _ { n } | P _ { n } ) \Rightarrow N ( - \sigma ^ { 2 } / 2 , \sigma ^ { 2 } )$ and then $\mathcal{L} ( \Lambda _ { n } | P _ { n } ^ { \prime } ) \Rightarrow N ( \sigma ^ { 2 } / 2 , \sigma ^ { 2 } )$ for some $\sigma > 0$. Also, if it so happens that $\mathcal{L} ( T _ { n } | P _ { n } ) \Rightarrow N ( 0 , \Gamma )$ and $\Lambda _ { n } - h ^ { \prime } T _ { n } \rightarrow - h ^ { \prime } \Gamma h / 2$ in $P_n$-probability for every $h$ in $\mathbf{R} ^ { k }$ (where $\square '$ denotes transpose and $\Gamma$ is a $k \times k$ positive-definite covariance matrix), then, under contiguity again, $\mathcal{L} ( T _ { n } | P _ { n } ^ { \prime } ) \Rightarrow N ( \Gamma h , \Gamma )$. |
| − | In the context of parametric models in statistics, contiguity results avail themselves in expanding (in the probability sense) a certain log-likelihood function, in obtaining its asymptotic distribution, in approximating the given family of probability measures by exponential probability measures in the neighbourhood of a parameter point, and in obtaining a convolution representation of the limiting probability measure of the distributions of certain estimates. All these results may then be exploited in deriving asymptotically optimal tests for certain statistical hypotheses testing problems (cf. [[Statistical hypotheses, verification of|Statistical hypotheses, verification of]]), and in studying the asymptotic efficiency (cf. also [[Efficiency, asymptotic|Efficiency, asymptotic]]) of estimates. In such a framework, random variables | + | In the context of parametric models in statistics, contiguity results avail themselves in expanding (in the probability sense) a certain log-likelihood function, in obtaining its asymptotic distribution, in approximating the given family of probability measures by exponential probability measures in the neighbourhood of a parameter point, and in obtaining a convolution representation of the limiting probability measure of the distributions of certain estimates. All these results may then be exploited in deriving asymptotically optimal tests for certain statistical hypotheses testing problems (cf. [[Statistical hypotheses, verification of|Statistical hypotheses, verification of]]), and in studying the asymptotic efficiency (cf. also [[Efficiency, asymptotic|Efficiency, asymptotic]]) of estimates. In such a framework, random variables $X _ { 0 } , \dots , X _ { n }$ are defined on $( \mathcal{X} , \mathcal{A} )$, $P _ { \theta }$ is a probability measure defined on $\mathcal{A}$ and depending on the parameter $\theta \in \Theta$, an open subset in $\mathbf{R} ^ { k }$, $P _ { n , \theta }$ is the restriction of $P _ { \theta }$ to $\mathcal{A} _ { n } = \sigma ( X _ { 0 } , \dots , X _ { n } )$, and the probability measures of interest are usually $P _ { n , \theta }$ and $P _ { n , \theta _ { n } }$, $\theta _ { n } = \theta + h / \sqrt { n }$. Under certain regularity conditions, $\{ P _ { n , \theta } \}$ and $\{ P _ { n , \theta _ { n }} \}$ are contiguous. The log-likelihood function $\Lambda _ { n } ( \theta ) = \operatorname { log } ( d P _ { n , \theta _ { n } } / P _ { n , \theta } )$ expands in $P _ { n , \theta }$ (and $P _ { n , \theta _ { n } }$-probability); thus: |
| − | + | \begin{equation*} \Lambda _ { n } ( \theta ) - h ^ { \prime } \Delta _ { n } ( \theta ) \rightarrow - \frac { 1 } { 2 } h ^ { \prime } \Gamma ( \theta ) h, \end{equation*} | |
| − | where | + | where $\Delta _ { n } ( \theta )$ is a $k$-dimensional random vector defined in terms of the derivative of an underlying probability density function, and $\Gamma ( \theta )$ is a covariance function. Furthermore, |
| − | + | \begin{equation*} \mathcal{L} [ \Delta _ { n } ( \theta ) | P _ { n , \theta } ] \Rightarrow N ( 0 , \Gamma ( \theta ) ), \end{equation*} | |
| − | + | \begin{equation*} \mathcal{L} [ \Lambda _ { n } ( \theta ) | P _ { n , \theta } ] \Rightarrow N \left( - \frac { 1 } { 2 } h ^ { \prime } \Gamma ( \theta ) h , h ^ { \prime } \Gamma ( \theta ) h \right) , \mathcal{L} [ \Lambda _ { n } ( \theta ) | P _ { n , \theta _ { n } } ] \Rightarrow N \left( \frac { 1 } { 2 } h ^ { \prime } \Gamma ( \theta ) h , h ^ { \prime } \Gamma ( \theta ) h \right), \end{equation*} | |
| − | + | \begin{equation*} \mathcal{L} [ \Delta _ { n } ( \theta ) | P _ { n , \theta _ { n } } ] \Rightarrow N ( \Gamma ( \theta ) h , \Gamma ( \theta ) ). \end{equation*} | |
| − | In addition, | + | In addition, $\| P _ { n , \theta _ { n }} - R _ { n , h }\| \rightarrow 0$ uniformly over bounded sets of $h$, where $R _ { n , h } ( A )$ is the normalized version of $\int _ { A } \operatorname { exp } ( h ^ { \prime } \Delta _ { n } ^ { * } ( \theta ) ) d P _ { n , \theta }$, $\Delta _ { n } ^ { * } ( \theta )$ being a suitably truncated version of $\Delta _ { n } ( \theta )$. Finally, for estimates $T _ { n }$ (of $\theta$) for which $\mathcal{L} [ \sqrt { n } ( T _ { n } - \theta _ { n } ) | P _ { n , \theta _ { n } } ] \Rightarrow \mathcal{L} ( \theta )$, a probability measure, one has $\mathcal{L} ( \theta ) = N ( 0 , \Gamma ^ { - 1 } ( \theta ) * \mathcal{L} _ { 2 } ( \theta ) )$, for a specified probability measure $\mathcal{L} _ { 2 } ( \theta )$. This last result is due to J. Hájek [[#References|[a3]]] (see also [[#References|[a6]]]). |
| − | Contiguity of two sequences of probability measures | + | Contiguity of two sequences of probability measures $\{ P _ { n , \theta } \}$ and $\{ P _ { n , \theta _ { n }} \}$, as defined above, may be generalized as follows: Replace $n$ by $\alpha _ { n }$, where $\{ \alpha _ { n } \} \subseteq \{ n \}$ converges to $\infty$ non-decreasingly, and replace $\theta _ { n }$ by $\theta _ { \tau _ { n } } = \theta + h \tau _ { n } ^ { - 1 / 2 }$, where $0 < \tau _ { n }$ are real numbers tending to $\infty$ non-decreasingly. Then, under suitable regularity conditions, $\{ P _ { \alpha _ { n } } , \theta \}$ and $\{ P _ { \alpha _ { n } , \theta _ { \tau _ { n } } } \}$ are contiguous if and only if $\alpha _ { n } / \tau _ { n } = O ( 1 )$ (see [[#References|[a1]]], Thm. 2.1). |
Some additional references to contiguity and its statistical applications are [[#References|[a4]]], [[#References|[a5]]], [[#References|[a2]]], [[#References|[a12]]], [[#References|[a10]]]. | Some additional references to contiguity and its statistical applications are [[#References|[a4]]], [[#References|[a5]]], [[#References|[a2]]], [[#References|[a12]]], [[#References|[a10]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> M.G. Akritas, M.L. Puri, G.G. Roussas, "Sample size, parameter rates and contiguity: the i.d.d. case" ''Commun. Statist. Theor. Meth.'' , '''A8''' : 1 (1979) pp. 71–83</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> P.E. Greenwood, A.M. Shiryayey, "Contiguity and the statistical invariance principle" , Gordon&Breach (1985)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J. Hájek, "A characterization of limiting distributions of regular estimates" ''Z. Wahrscheinlichkeitsth. verw. Gebiete'' , '''14''' (1970) pp. 323–330</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> J. Hájek, Z. Sidak, "Theory of rank tests" , Acad. Press (1967)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> I.A. Ibragimov, R.Z. Has'minskii, "Statistical estimation" , Springer (1981)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> N. Inagaki, "On the limiting distribution of a sequence of estimators with uniformity property" ''Ann. Inst. Statist. Math.'' , '''22''' (1970) pp. 1–13</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> L. Le Cam, "Locally asymptotically normal families of distributions" ''Univ. Calif. Publ. in Statist.'' , '''3''' (1960) pp. 37–98</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> L. Le Cam, "Asymptotic methods in statistical decision theory" , Springer (1986)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> L. Le Cam, G.L. Yang, "Asymptotics in statistics: some basic concepts" , Springer (1990)</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> J. Pfanzagl, "Parametric statistical inference" , W. de Gruyter (1994)</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> G.G. Roussas, "Contiguity of probability measures: some applications in statistics" , Cambridge Univ. Press (1972)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> H. Strasser, "Mathematical theory of statistics" , W. de Gruyter (1985)</td></tr></table> |
Revision as of 17:03, 1 July 2020
The concept of contiguity was formally introduced and developed by L. Le Cam in [a7]. It refers to sequences of probability measures, and is meant to be a measure of "closeness" or "nearness" of such sequences (cf. also Probability measure). It may also be viewed as a kind of uniform asymptotic mutual absolute continuity of probability measures. Actually, the need for the introduction of such a concept arose as early as 1955 or 1956, and it was at that time that Le Cam selected the name of "contiguity" , with the help of J.D. Esary (see [a9], p. 29).
There are several equivalent characterizations of contiguity, and the following may serve as its definition. Two sequences $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ are said to be contiguous if for any $A _ { n } \in\mathcal{ A} _ { n }$ for which $P _ { n } ( A _ { n } ) \rightarrow 0$, it also happens that $P _ { n } ^ { \prime } ( A _ { n } ) \rightarrow 0$, and vice versa, where $( {\cal X , A} _ { n } )$ is a sequence of measurable spaces and $P_n$ and $P _ { n } ^ { \prime }$ are measures on $\mathcal{A} _ { n }$. Here and in the sequel, all limits are taken as $n \rightarrow \infty$. It is worth mentioning at this point that contiguity is transitive: If $\{ P _ { n } \}$, $\{ P _ { n } ^ { \prime } \}$ are contiguous and $\{ P _ { n } ^ { \prime } \}$, $\{ P _ { n } ^ { \prime \prime } \}$ are contiguous, then so are $\{ P _ { n } \}$, $\{ P _ { n } ^ { \prime \prime } \}$. Contiguity simplifies many arguments in passing to the limit, and it plays a major role in the asymptotic theory of statistical inference (cf. also Statistical hypotheses, verification of). Thus, contiguity is used in parts of [a8] as a tool of obtaining asymptotic results in an elegant manner; [a9] is a more accessible general reference on contiguity and its usages. In a Markovian framework, contiguity, some related results and selected statistical applications are discussed in [a11]. For illustrative purposes, [a11] can be used as standard reference.
The definition of contiguity calls for its comparison with more familiar modes of "closeness" , such as that based on the $\operatorname {sup}$ (or $L_1$) norm, defined by
\begin{equation*} \| P _ { n } - P _ { n } ^ { \prime } \| = 2 \operatorname { sup } \{ | P _ { n } ( A ) - P _ { n } ^ { \prime } ( A ) | : A \in \mathcal{A} _ { n } \}, \end{equation*}
and also the concept of mutual absolute continuity (cf. also Absolute continuity), $P _ { n } \approx P _ { n } ^ { \prime }$. It is always true that convergence in the $L_1$-norm implies contiguity, but the converse is not true (see, e.g., [a11], p. 12; the special case of Example 3.1(i)). So, contiguity is a weaker measure of "closeness" of two sequences of probability measures than that provided by sup-norm convergence. Also, by means of examples, it may be illustrated that it can happen that $P _ { n } \approx P _ { n } ^ { \prime }$ for all $n$ (i.e., $P _ { n } ( A ) = 0$ if and only if $P _ { n } ^ { \prime } ( A ) = 0$ for all $n$, $A \in {\cal A} _ { n }$) whereas $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ are not contiguous (see, e.g., [a11], pp. 9–10; Example 2.2). That contiguity need not imply absolute continuity for any $n$ is again demonstrated by examples (see, e.g., [a11], p. 9; Example 2.1 and Remark 2.3). This should not come as a surprise, since contiguity is interpreted as asymptotic absolute continuity rather than absolute continuity for any finite $n$. It is to be noted, however, that a pair of contiguous sequences of probability measures can always be replaced by another pair of contiguous sequences whose respective members are mutually absolutely continuous and lie arbitrarily close to the given ones in the sup-norm sense (see, e.g., [a11], p. 25–26; Thm. 5.1).
The concept exactly opposite to contiguity is that of (asymptotic) entire separation. Thus, two sequences $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ are said to be (asymptotically) entirely separated if there exist $\{ m \} \subseteq \{ n \}$ and 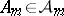 such that $P _ { m } ( A _ { m } ) \rightarrow 0$ whereas $P _ { m } ^ { \prime } ( A _ { m } ) \rightarrow 1$ as $m \rightarrow \infty$ (see [a2], p. 24).
such that $P _ { m } ( A _ { m } ) \rightarrow 0$ whereas $P _ { m } ^ { \prime } ( A _ { m } ) \rightarrow 1$ as $m \rightarrow \infty$ (see [a2], p. 24).
Alternative characterizations of contiguity are provided in [a11], Def. 2.1; Prop. 3.1; Prop. 6.1. In terms of sequences of random variables $\{ T _ { n } \}$, two sequences $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ are contiguous if $T _ { n } \rightarrow 0$ in $P_n$-probability implies $T _ { n } \rightarrow 0$ in $P _ { n } ^ { \prime }$-probability, and vice versa (cf. also Random variable). Thus, under contiguity, convergence in probability of sequences of random variables under $P_n$ and $P _ { n } ^ { \prime }$ are equivalent and the limits are the same. Actually, contiguity of $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ is determined by the behaviour of the sequences of probability measures $\{ \mathcal{L} _ { n } \}$ and $\{ {\cal L} _ { n } ^ { \prime } \}$, where $\mathcal{L} _ { n } = \mathcal{L} ( \Lambda _ { n } | P _ { n } )$, $\mathcal{L} _ { n } ^ { \prime } = \mathcal{L} ( \Lambda _ { n } | P _ { n } ^ { \prime } )$ and $\Lambda _ { n } = \operatorname { log } ( d P _ { n } ^ { \prime } / d P _ { n } )$. As explained above, there is no loss in generality by supposing that $P_n$ and $P _ { n } ^ { \prime }$ are mutually absolutely continuous for all $n$, and thus the log-likelihood function $\Lambda _ { n }$ is well-defined with $P_n$-probability $1$ for all $n$. Then, e.g., $\{ P _ { n } \}$ and $\{ P _ { n } ^ { \prime } \}$ are contiguous if and only if $\{ \mathcal{L} _ { n } \}$ and $\{ {\cal L} _ { n } ^ { \prime } \}$ are relatively compact, or $\{ \mathcal{L} _ { n } \}$ is relatively compact and for every subsequence $\{ \mathcal{L} _ { m } \}$ converging weakly to a probability measure $\mathcal{L}$, one has $\int \operatorname { exp } \lambda d \mathcal{L} = 1$, where $\lambda$ is a dummy variable. It should be noted at this point that, under contiguity, the asymptotic distributions, under $P_n$ and $P _ { n } ^ { \prime }$, of the likelihood (or log-likelihood) ratios $d P _ { n } ^ { \prime } / d P_n$ are non-degenerate and distinct. Therefore, the statistical problem of choosing between $P_n$ and $P _ { n } ^ { \prime }$ is non-trivial for all sufficiently large $n$.
An important consequence of contiguity is the following. With $\Lambda _ { n }$ as above, let $T _ { n }$ be a $k$-dimensional random vector such that $\mathcal{L} [ ( \Lambda _ { n } , T _ { n } ) | P _ { n } ] \Rightarrow \tilde{\mathcal{L}}$, a probability measure (where "" stands for weak convergence of probability measures). Then $\mathcal{L} [ ( \Lambda _ { n } , T _ { n } ) | P _ { n } ^ { \prime } ] \Rightarrow \tilde{\mathcal{L}} ^ { \prime }$ and $\widetilde{ \cal L}'$ is determined by $d \tilde{L} ^ { \prime } / d \tilde{L} = \operatorname { exp } \lambda$. In particular, one may determine the asymptotic distribution of $\Lambda _ { n }$ under (the alternative hypothesis) $P _ { n } ^ { \prime }$ in terms of the asymptotic distribution of $\Lambda _ { n }$ under (the null hypothesis) $P_n$. Typically, $\mathcal{L} ( \Lambda _ { n } | P _ { n } ) \Rightarrow N ( - \sigma ^ { 2 } / 2 , \sigma ^ { 2 } )$ and then $\mathcal{L} ( \Lambda _ { n } | P _ { n } ^ { \prime } ) \Rightarrow N ( \sigma ^ { 2 } / 2 , \sigma ^ { 2 } )$ for some $\sigma > 0$. Also, if it so happens that $\mathcal{L} ( T _ { n } | P _ { n } ) \Rightarrow N ( 0 , \Gamma )$ and $\Lambda _ { n } - h ^ { \prime } T _ { n } \rightarrow - h ^ { \prime } \Gamma h / 2$ in $P_n$-probability for every $h$ in $\mathbf{R} ^ { k }$ (where $\square '$ denotes transpose and $\Gamma$ is a $k \times k$ positive-definite covariance matrix), then, under contiguity again, $\mathcal{L} ( T _ { n } | P _ { n } ^ { \prime } ) \Rightarrow N ( \Gamma h , \Gamma )$.
In the context of parametric models in statistics, contiguity results avail themselves in expanding (in the probability sense) a certain log-likelihood function, in obtaining its asymptotic distribution, in approximating the given family of probability measures by exponential probability measures in the neighbourhood of a parameter point, and in obtaining a convolution representation of the limiting probability measure of the distributions of certain estimates. All these results may then be exploited in deriving asymptotically optimal tests for certain statistical hypotheses testing problems (cf. Statistical hypotheses, verification of), and in studying the asymptotic efficiency (cf. also Efficiency, asymptotic) of estimates. In such a framework, random variables $X _ { 0 } , \dots , X _ { n }$ are defined on $( \mathcal{X} , \mathcal{A} )$, $P _ { \theta }$ is a probability measure defined on $\mathcal{A}$ and depending on the parameter $\theta \in \Theta$, an open subset in $\mathbf{R} ^ { k }$, $P _ { n , \theta }$ is the restriction of $P _ { \theta }$ to $\mathcal{A} _ { n } = \sigma ( X _ { 0 } , \dots , X _ { n } )$, and the probability measures of interest are usually $P _ { n , \theta }$ and $P _ { n , \theta _ { n } }$, $\theta _ { n } = \theta + h / \sqrt { n }$. Under certain regularity conditions, $\{ P _ { n , \theta } \}$ and $\{ P _ { n , \theta _ { n }} \}$ are contiguous. The log-likelihood function $\Lambda _ { n } ( \theta ) = \operatorname { log } ( d P _ { n , \theta _ { n } } / P _ { n , \theta } )$ expands in $P _ { n , \theta }$ (and $P _ { n , \theta _ { n } }$-probability); thus:
\begin{equation*} \Lambda _ { n } ( \theta ) - h ^ { \prime } \Delta _ { n } ( \theta ) \rightarrow - \frac { 1 } { 2 } h ^ { \prime } \Gamma ( \theta ) h, \end{equation*}
where $\Delta _ { n } ( \theta )$ is a $k$-dimensional random vector defined in terms of the derivative of an underlying probability density function, and $\Gamma ( \theta )$ is a covariance function. Furthermore,
\begin{equation*} \mathcal{L} [ \Delta _ { n } ( \theta ) | P _ { n , \theta } ] \Rightarrow N ( 0 , \Gamma ( \theta ) ), \end{equation*}
\begin{equation*} \mathcal{L} [ \Lambda _ { n } ( \theta ) | P _ { n , \theta } ] \Rightarrow N \left( - \frac { 1 } { 2 } h ^ { \prime } \Gamma ( \theta ) h , h ^ { \prime } \Gamma ( \theta ) h \right) , \mathcal{L} [ \Lambda _ { n } ( \theta ) | P _ { n , \theta _ { n } } ] \Rightarrow N \left( \frac { 1 } { 2 } h ^ { \prime } \Gamma ( \theta ) h , h ^ { \prime } \Gamma ( \theta ) h \right), \end{equation*}
\begin{equation*} \mathcal{L} [ \Delta _ { n } ( \theta ) | P _ { n , \theta _ { n } } ] \Rightarrow N ( \Gamma ( \theta ) h , \Gamma ( \theta ) ). \end{equation*}
In addition, $\| P _ { n , \theta _ { n }} - R _ { n , h }\| \rightarrow 0$ uniformly over bounded sets of $h$, where $R _ { n , h } ( A )$ is the normalized version of $\int _ { A } \operatorname { exp } ( h ^ { \prime } \Delta _ { n } ^ { * } ( \theta ) ) d P _ { n , \theta }$, $\Delta _ { n } ^ { * } ( \theta )$ being a suitably truncated version of $\Delta _ { n } ( \theta )$. Finally, for estimates $T _ { n }$ (of $\theta$) for which $\mathcal{L} [ \sqrt { n } ( T _ { n } - \theta _ { n } ) | P _ { n , \theta _ { n } } ] \Rightarrow \mathcal{L} ( \theta )$, a probability measure, one has $\mathcal{L} ( \theta ) = N ( 0 , \Gamma ^ { - 1 } ( \theta ) * \mathcal{L} _ { 2 } ( \theta ) )$, for a specified probability measure $\mathcal{L} _ { 2 } ( \theta )$. This last result is due to J. Hájek [a3] (see also [a6]).
Contiguity of two sequences of probability measures $\{ P _ { n , \theta } \}$ and $\{ P _ { n , \theta _ { n }} \}$, as defined above, may be generalized as follows: Replace $n$ by $\alpha _ { n }$, where $\{ \alpha _ { n } \} \subseteq \{ n \}$ converges to $\infty$ non-decreasingly, and replace $\theta _ { n }$ by $\theta _ { \tau _ { n } } = \theta + h \tau _ { n } ^ { - 1 / 2 }$, where $0 < \tau _ { n }$ are real numbers tending to $\infty$ non-decreasingly. Then, under suitable regularity conditions, $\{ P _ { \alpha _ { n } } , \theta \}$ and $\{ P _ { \alpha _ { n } , \theta _ { \tau _ { n } } } \}$ are contiguous if and only if $\alpha _ { n } / \tau _ { n } = O ( 1 )$ (see [a1], Thm. 2.1).
Some additional references to contiguity and its statistical applications are [a4], [a5], [a2], [a12], [a10].
References
| [a1] | M.G. Akritas, M.L. Puri, G.G. Roussas, "Sample size, parameter rates and contiguity: the i.d.d. case" Commun. Statist. Theor. Meth. , A8 : 1 (1979) pp. 71–83 |
| [a2] | P.E. Greenwood, A.M. Shiryayey, "Contiguity and the statistical invariance principle" , Gordon&Breach (1985) |
| [a3] | J. Hájek, "A characterization of limiting distributions of regular estimates" Z. Wahrscheinlichkeitsth. verw. Gebiete , 14 (1970) pp. 323–330 |
| [a4] | J. Hájek, Z. Sidak, "Theory of rank tests" , Acad. Press (1967) |
| [a5] | I.A. Ibragimov, R.Z. Has'minskii, "Statistical estimation" , Springer (1981) |
| [a6] | N. Inagaki, "On the limiting distribution of a sequence of estimators with uniformity property" Ann. Inst. Statist. Math. , 22 (1970) pp. 1–13 |
| [a7] | L. Le Cam, "Locally asymptotically normal families of distributions" Univ. Calif. Publ. in Statist. , 3 (1960) pp. 37–98 |
| [a8] | L. Le Cam, "Asymptotic methods in statistical decision theory" , Springer (1986) |
| [a9] | L. Le Cam, G.L. Yang, "Asymptotics in statistics: some basic concepts" , Springer (1990) |
| [a10] | J. Pfanzagl, "Parametric statistical inference" , W. de Gruyter (1994) |
| [a11] | G.G. Roussas, "Contiguity of probability measures: some applications in statistics" , Cambridge Univ. Press (1972) |
| [a12] | H. Strasser, "Mathematical theory of statistics" , W. de Gruyter (1985) |
Contiguity of probability measures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contiguity_of_probability_measures&oldid=50484