Difference between revisions of "Lannes-T-functor"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 98 formulas out of 100 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 100 formulas, 98 were replaced by TEX code.--> | |
| − | The | + | {{TEX|semi-auto}}{{TEX|partial}} |
| + | The calculation of the homotopy type of the space of continuous mappings $\operatorname{Map}( X , Y )$ is a fundamental problem of [[Homotopy|homotopy]] theory. The set of path components, $\pi_0 \; \operatorname { Map } ( X , Y ) = [ X , Y ]$ corresponds to the homotopy classes of such mappings. There are relatively few cases for which this information is explicitly known (as of 1998). A major impact of the work [[#References|[a1]]] of J. Lannes on unstable modules and the T-functor has been to expand this knowledge to include many cases in which the sources and targets are classifying spaces of finite and compact Lie groups (cf. also [[Lie group|Lie group]]). | ||
| − | + | The work of N. Steenrod and others assigns in a natural way to each [[Topological space|topological space]] $X$ and each prime number $p$ an algebraic model, consisting of a [[Graded algebra|graded algebra]] $H ^ { * } ( X , \mathbf{F} _ { p } ) = R ^ { * }$ over $\mathbf{F} _ { p }$ and an algebra $\mathcal{A} _ { p }$ of natural operations, called the Steenrod algebra. Each $f : X \rightarrow Y$ induces an element $f ^ { * } \in \text { Hom}_{\text{alg} } ( H ^ { * } ( Y , {\bf F} _ { p } ) , H ^ { * } ( X , {\bf F} _ { p } ) )$ that commutes with the action of $\mathcal{A} _ { p }$. $\mathcal{A} _ { p }$ is a connected graded [[Hopf algebra|Hopf algebra]] acting on the graded algebra $R ^ { * }$. | |
| − | The | + | The hypothesis that $R ^ { * }$ is the [[Cohomology|cohomology]] of a space imposes an additional "unstable" condition. This is most simply stated if $p = 2$: ${\cal A} _ { 2 }$ is generated as an (non-commutative) algebra by the Steenrod operations $\{ \mathcal{S} \operatorname {q} ^ { i } : i \geq 0 \}$, with relations forced by its actions of the cohomology of all topological spaces. For example, $\mathcal{S} \text{q} ^ { 0 } = \operatorname{Id}$ and $\mathcal{S} \text{q} ^ { 1 } = \beta$, the modulo-$2$ Bockstein operator. The unstable condition is then that ${\cal S} \operatorname {q} ^ { i } x _ { n } = 0$ for $i > n$ and $\mathcal{S} \operatorname{q} ^ { n } x _ { n } = x _ { n } ^ { 2 }$. The algebraic category $\mathcal{K}$ of unstable algebras $\{ \mathcal{R} ^ { * } \}$ over $\mathcal{A} _ { p }$ is thus an approximation to the homotopy category of topological spaces. The larger category $\mathcal U$ of unstable modules over $\mathcal{A} _ { p }$ has also proved useful. |
| − | + | For $p > 2$, the structure of $\mathcal{A} _ { p }$ and unstable actions are similar, but slightly more involved. However, in all cases, the set of relations in the Steenrod algebra and the unstable condition are derivable from the known action of $\mathcal{A} _ { p }$ on the cohomology of products of copies of $B {\bf Z} / p {\bf Z}$. In the following, explicit references to the coefficients are omitted. | |
| + | |||
| + | The relationship of $\pi _0 \operatorname { Map } ( X , Y )$ to its model $\operatorname{Hom}_{ \mathcal{K} } ( H ^ { * } ( Y , \mathbf{F} _ { p } ) , H ^ { * } ( X , \mathbf{F} _ { p } ) )$ is of particular interest. The equivalence | ||
| + | |||
| + | \begin{equation*} \operatorname { Map } ( X \times Z , Y ) \rightarrow \operatorname { Map } ( X , \operatorname { Map } ( Z , Y ) ) \end{equation*} | ||
raises the hope that in very favourable cases the mapping | raises the hope that in very favourable cases the mapping | ||
| − | + | \begin{equation*} \operatorname{Hom}_{\mathcal{K}} ( H ^ { * } \operatorname { Map } ( Z , Y ) , H ^ { * } X ) \rightarrow \end{equation*} | |
| − | + | \begin{equation*} \rightarrow \operatorname{Hom}_{\mathcal{K}} ( H ^ { * } Y , H ^ { * } X \bigotimes H ^ { * } Z ) \end{equation*} | |
| − | might be an isomorphism. That suggests that in the category | + | might be an isomorphism. That suggests that in the category $\mathcal{K}$, $H ^ { * } \operatorname { Map } ( Z , Y )$ should be approximated by the left adjoint functor to tensoring on the right by $H ^ { * } Z$. This motivated J. Lannes to define the functor $T$ as follows: If $E$ is a finite-dimensional $\mathbf{F} _ { p }$-vector space, then the $T$-functor $T _ { E } : \mathcal{U} \rightarrow \mathcal{U} $ is the left adjoint in $\mathcal U$ of the functor $( ( _- ) \otimes _ {{\bf F}_p } H ^ { * } B V ) :\cal U \rightarrow U$. In the topological case, there is a natural mapping |
| − | + | \begin{equation*} \lambda _ { X } : T _ { E } H ^ { * } X \rightarrow H ^ { * } \operatorname { Map } ( B E , X ). \end{equation*} | |
| − | For general | + | For general $Z$, the adjoint to $( ( \_ ) \otimes _ { \mathbf{F}_p } H ^ { * } Z )$ accounts for only part of the starting page of a Bousfield–Kan unstable Adams spectral sequence for $\operatorname{Map}( Z , Y )$. Lannes provides the basic connection to topology by blending the algebraic properties of $T _ { E }$ and $\mathcal{K}$ with the Bousfield–Kan spectral sequence: For many interesting spaces $X$, |
| − | + | \begin{equation*} H ^ { * } \operatorname { Map } ( B E , X ) \approx T _ { E } H ^ { * } X. \end{equation*} | |
In particular, | In particular, | ||
| − | + | \begin{equation*} \pi _ { 0 } \operatorname { Map } ( B E , X ) = [ B E , X ] = \operatorname { Hom } _ { \mathcal{K} } ( H ^ { * } X , H ^ { * } B E ). \end{equation*} | |
| − | For | + | For $f : X \rightarrow Y$, one has the path component $\operatorname{Map}( X , Y ) _ { f }$ of functions homotopic to $f$. The analogous $T$-construct is as follows: Each $\varphi \in \operatorname{Hom}_{\mathcal{K}}( R ^ { * } , H ^ { * } B E )$ induces a $T ^ { 0 } E$-module structure on $\mathbf{F} _ { p }$ and |
| − | + | \begin{equation*} T _ { E , \varphi } R ^ { * } = T _ { E } R ^ { * } \bigotimes _ { T ^ { 0 } E } \mathbf{F} _ { p }. \end{equation*} | |
| − | The most striking features of | + | The most striking features of $T _ { E }$ are summarized below (see also [[#References|[a1]]]). To some extent, these were presaged by work of G. Carlsson and H.T. Miller, who established that the $\{ H ^ { * } B V \}$ are injectives in $\mathcal U$. |
| − | a) | + | a) $T _ { E }$ is exact. |
| − | b) | + | b) $T _ { E }$ respects tensor products, i.e $T _ { E } ( M \otimes _ { \mathbf{F}_ p} N) = T _ { E } M \otimes _ { \mathbf{F}_ p} T _ { E } N$. |
| − | c) | + | c) $T _ { E }$ commutes with the $p$th power operations in a suitable sense. |
| − | d) | + | d) $T _ { E }$ maps $\mathcal{K}$ to $\mathcal{K}$. |
| − | In principle, | + | In principle, $T _ { E } M ^ { * }$ can be calculated by using the exactness property and a resolution of $M ^ { * }$ by free unstable $\mathcal{A} _ { p }$-modules. In practice, other methods are often more effective; for example, |
| − | 1) If | + | 1) If $M ^ { * }$ is finite, then $T _ { E } M ^ { * } = M ^ { * }$. |
| − | 2) If | + | 2) If $R ^ { * } = H ^ { * } B V$, then |
| − | + | \begin{equation*} T _ { E } R ^ { * } = \prod _ { \text { Hom}_{ \text{grp} } ( E , V ) } H ^ { * } B V, \end{equation*} | |
| − | for | + | for $E$ and $V$ finite-dimensional $\mathbf{F} _ { p }$-vector spaces. |
| − | 3) If | + | 3) If $\tau : R ^ { * } \rightarrow H ^ { * } B E$ in $\mathcal{K}$ is an inclusion, then $T _ { E , \tau } R ^ { * }$ is the smallest sub-Hopf algebra of $H ^ { * } B E$ that contains $\tau ( R ^ { * } )$. |
| − | 4) If | + | 4) If $X$ is a finite $E$-complex with fixed point set $X ^ { E }$ and $H ^ { *_{E}} X$ is the modulo $p$ cohomology of the Borel construction, then $T_{E, \text{id}} H _ { E } ^ { * } X = H ^ { * } B E \otimes _ { \text{F}_ p } H ^ { * } X ^ { E }$ in $\mathcal{K}$. |
| − | 5) If | + | 5) If $G$ is a compact [[Lie group|Lie group]], then |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l120/l120030/l120030100.png"/></td> </tr></table> |
These examples each have powerful topological consequences. For example, the first and fourth lead to new proofs of the Sullivan conjecture, originally proved by Miller and Carlsson. The last leads to a new view of the homotopy theory of classifying spaces. Most of the above is referenced in [[#References|[a2]]]. | These examples each have powerful topological consequences. For example, the first and fourth lead to new proofs of the Sullivan conjecture, originally proved by Miller and Carlsson. The last leads to a new view of the homotopy theory of classifying spaces. Most of the above is referenced in [[#References|[a2]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J. Lannes, "Sur les espaces fonctionnels dont la source est le classifiant d'un $p$-groupe abélien élémentaire" ''Inst. Hautes Etudes Sci. Publ. Math.'' , '''75''' (1992) pp. 135–244 (Appendix by M. Zisman)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> L. Schwartz, "Unstable modules over the Steenrod algebra and Sullivan's fixed point set conjecture" , Univ. Chicago Press (1994)</td></tr></table> |
Revision as of 17:00, 1 July 2020
The calculation of the homotopy type of the space of continuous mappings $\operatorname{Map}( X , Y )$ is a fundamental problem of homotopy theory. The set of path components, $\pi_0 \; \operatorname { Map } ( X , Y ) = [ X , Y ]$ corresponds to the homotopy classes of such mappings. There are relatively few cases for which this information is explicitly known (as of 1998). A major impact of the work [a1] of J. Lannes on unstable modules and the T-functor has been to expand this knowledge to include many cases in which the sources and targets are classifying spaces of finite and compact Lie groups (cf. also Lie group).
The work of N. Steenrod and others assigns in a natural way to each topological space $X$ and each prime number $p$ an algebraic model, consisting of a graded algebra $H ^ { * } ( X , \mathbf{F} _ { p } ) = R ^ { * }$ over $\mathbf{F} _ { p }$ and an algebra $\mathcal{A} _ { p }$ of natural operations, called the Steenrod algebra. Each $f : X \rightarrow Y$ induces an element $f ^ { * } \in \text { Hom}_{\text{alg} } ( H ^ { * } ( Y , {\bf F} _ { p } ) , H ^ { * } ( X , {\bf F} _ { p } ) )$ that commutes with the action of $\mathcal{A} _ { p }$. $\mathcal{A} _ { p }$ is a connected graded Hopf algebra acting on the graded algebra $R ^ { * }$.
The hypothesis that $R ^ { * }$ is the cohomology of a space imposes an additional "unstable" condition. This is most simply stated if $p = 2$: ${\cal A} _ { 2 }$ is generated as an (non-commutative) algebra by the Steenrod operations $\{ \mathcal{S} \operatorname {q} ^ { i } : i \geq 0 \}$, with relations forced by its actions of the cohomology of all topological spaces. For example, $\mathcal{S} \text{q} ^ { 0 } = \operatorname{Id}$ and $\mathcal{S} \text{q} ^ { 1 } = \beta$, the modulo-$2$ Bockstein operator. The unstable condition is then that ${\cal S} \operatorname {q} ^ { i } x _ { n } = 0$ for $i > n$ and $\mathcal{S} \operatorname{q} ^ { n } x _ { n } = x _ { n } ^ { 2 }$. The algebraic category $\mathcal{K}$ of unstable algebras $\{ \mathcal{R} ^ { * } \}$ over $\mathcal{A} _ { p }$ is thus an approximation to the homotopy category of topological spaces. The larger category $\mathcal U$ of unstable modules over $\mathcal{A} _ { p }$ has also proved useful.
For $p > 2$, the structure of $\mathcal{A} _ { p }$ and unstable actions are similar, but slightly more involved. However, in all cases, the set of relations in the Steenrod algebra and the unstable condition are derivable from the known action of $\mathcal{A} _ { p }$ on the cohomology of products of copies of $B {\bf Z} / p {\bf Z}$. In the following, explicit references to the coefficients are omitted.
The relationship of $\pi _0 \operatorname { Map } ( X , Y )$ to its model $\operatorname{Hom}_{ \mathcal{K} } ( H ^ { * } ( Y , \mathbf{F} _ { p } ) , H ^ { * } ( X , \mathbf{F} _ { p } ) )$ is of particular interest. The equivalence
\begin{equation*} \operatorname { Map } ( X \times Z , Y ) \rightarrow \operatorname { Map } ( X , \operatorname { Map } ( Z , Y ) ) \end{equation*}
raises the hope that in very favourable cases the mapping
\begin{equation*} \operatorname{Hom}_{\mathcal{K}} ( H ^ { * } \operatorname { Map } ( Z , Y ) , H ^ { * } X ) \rightarrow \end{equation*}
\begin{equation*} \rightarrow \operatorname{Hom}_{\mathcal{K}} ( H ^ { * } Y , H ^ { * } X \bigotimes H ^ { * } Z ) \end{equation*}
might be an isomorphism. That suggests that in the category $\mathcal{K}$, $H ^ { * } \operatorname { Map } ( Z , Y )$ should be approximated by the left adjoint functor to tensoring on the right by $H ^ { * } Z$. This motivated J. Lannes to define the functor $T$ as follows: If $E$ is a finite-dimensional $\mathbf{F} _ { p }$-vector space, then the $T$-functor $T _ { E } : \mathcal{U} \rightarrow \mathcal{U} $ is the left adjoint in $\mathcal U$ of the functor $( ( _- ) \otimes _ {{\bf F}_p } H ^ { * } B V ) :\cal U \rightarrow U$. In the topological case, there is a natural mapping
\begin{equation*} \lambda _ { X } : T _ { E } H ^ { * } X \rightarrow H ^ { * } \operatorname { Map } ( B E , X ). \end{equation*}
For general $Z$, the adjoint to $( ( \_ ) \otimes _ { \mathbf{F}_p } H ^ { * } Z )$ accounts for only part of the starting page of a Bousfield–Kan unstable Adams spectral sequence for $\operatorname{Map}( Z , Y )$. Lannes provides the basic connection to topology by blending the algebraic properties of $T _ { E }$ and $\mathcal{K}$ with the Bousfield–Kan spectral sequence: For many interesting spaces $X$,
\begin{equation*} H ^ { * } \operatorname { Map } ( B E , X ) \approx T _ { E } H ^ { * } X. \end{equation*}
In particular,
\begin{equation*} \pi _ { 0 } \operatorname { Map } ( B E , X ) = [ B E , X ] = \operatorname { Hom } _ { \mathcal{K} } ( H ^ { * } X , H ^ { * } B E ). \end{equation*}
For $f : X \rightarrow Y$, one has the path component $\operatorname{Map}( X , Y ) _ { f }$ of functions homotopic to $f$. The analogous $T$-construct is as follows: Each $\varphi \in \operatorname{Hom}_{\mathcal{K}}( R ^ { * } , H ^ { * } B E )$ induces a $T ^ { 0 } E$-module structure on $\mathbf{F} _ { p }$ and
\begin{equation*} T _ { E , \varphi } R ^ { * } = T _ { E } R ^ { * } \bigotimes _ { T ^ { 0 } E } \mathbf{F} _ { p }. \end{equation*}
The most striking features of $T _ { E }$ are summarized below (see also [a1]). To some extent, these were presaged by work of G. Carlsson and H.T. Miller, who established that the $\{ H ^ { * } B V \}$ are injectives in $\mathcal U$.
a) $T _ { E }$ is exact.
b) $T _ { E }$ respects tensor products, i.e $T _ { E } ( M \otimes _ { \mathbf{F}_ p} N) = T _ { E } M \otimes _ { \mathbf{F}_ p} T _ { E } N$.
c) $T _ { E }$ commutes with the $p$th power operations in a suitable sense.
d) $T _ { E }$ maps $\mathcal{K}$ to $\mathcal{K}$.
In principle, $T _ { E } M ^ { * }$ can be calculated by using the exactness property and a resolution of $M ^ { * }$ by free unstable $\mathcal{A} _ { p }$-modules. In practice, other methods are often more effective; for example,
1) If $M ^ { * }$ is finite, then $T _ { E } M ^ { * } = M ^ { * }$.
2) If $R ^ { * } = H ^ { * } B V$, then
\begin{equation*} T _ { E } R ^ { * } = \prod _ { \text { Hom}_{ \text{grp} } ( E , V ) } H ^ { * } B V, \end{equation*}
for $E$ and $V$ finite-dimensional $\mathbf{F} _ { p }$-vector spaces.
3) If $\tau : R ^ { * } \rightarrow H ^ { * } B E$ in $\mathcal{K}$ is an inclusion, then $T _ { E , \tau } R ^ { * }$ is the smallest sub-Hopf algebra of $H ^ { * } B E$ that contains $\tau ( R ^ { * } )$.
4) If $X$ is a finite $E$-complex with fixed point set $X ^ { E }$ and $H ^ { *_{E}} X$ is the modulo $p$ cohomology of the Borel construction, then $T_{E, \text{id}} H _ { E } ^ { * } X = H ^ { * } B E \otimes _ { \text{F}_ p } H ^ { * } X ^ { E }$ in $\mathcal{K}$.
5) If $G$ is a compact Lie group, then
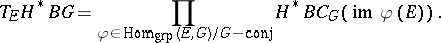 |
These examples each have powerful topological consequences. For example, the first and fourth lead to new proofs of the Sullivan conjecture, originally proved by Miller and Carlsson. The last leads to a new view of the homotopy theory of classifying spaces. Most of the above is referenced in [a2].
References
| [a1] | J. Lannes, "Sur les espaces fonctionnels dont la source est le classifiant d'un $p$-groupe abélien élémentaire" Inst. Hautes Etudes Sci. Publ. Math. , 75 (1992) pp. 135–244 (Appendix by M. Zisman) |
| [a2] | L. Schwartz, "Unstable modules over the Steenrod algebra and Sullivan's fixed point set conjecture" , Univ. Chicago Press (1994) |
Lannes-T-functor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lannes-T-functor&oldid=50376