Difference between revisions of "Weil algebra of a Lie algebra"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (AUTOMATIC EDIT (latexlist): Replaced 20 formulas out of 23 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 23 formulas, 20 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | Let $G$ be a connected [[Lie group|Lie group]] with [[Lie algebra|Lie algebra]] $\frak g$. The Weil algebra $W ( \mathfrak{g} )$ of $\frak g$ was first introduced in a series of seminars by H. Cartan [[#References|[a1]]], in part based on some unpublished work of A. Weil. As a differential [[Graded algebra|graded algebra]], it is given by the tensor product | ||
| − | + | \begin{equation*} W ( \mathfrak { g } ) = \bigwedge \mathfrak { g } ^ { * } \bigotimes S \mathfrak { g } ^ { * }, \end{equation*} | |
| − | + | where $\wedge \mathfrak { g } ^ { * }$ and $S \mathfrak { g } ^ { * }$ denote the exterior and symmetric algebras, respectively (cf. also [[Exterior algebra|Exterior algebra]]; [[Symmetric algebra|Symmetric algebra]]). | |
| − | + | The Weil algebra and its generalizations have been studied extensively by F.W. Kamber and Ph. Tondeur [[#References|[a3]]] [[#References|[a4]]]. Let $K \subseteq G$ be a maximal compact subgroup, with $\frak p$ denoting the Lie algebra of $K$. The relative Weil algebra for $( G , K )$ is defined by | |
| − | + | \begin{equation*} W ( G , K ) = \{ \bigwedge ( \mathfrak { g } / \mathfrak { k } ) ^ { * } \bigotimes S \mathfrak { g } ^ { * } \} ^ { K }. \end{equation*} | |
| − | + | With regards to the universal classifying bundle $E G \rightarrow B G$ (cf. also [[Bundle|Bundle]]; [[Classifying space|Classifying space]]; [[Universal space|Universal space]]), there are canonical isomorphisms in [[Cohomology|cohomology]] | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130050/w13005014.png"/></td> </tr></table> |
| − | + | where $I ( K )$ denotes the $\operatorname{Ad} K$-invariant polynomials. For a given integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130050/w13005017.png"/>, one has the ideal | |
| − | + | \begin{equation*} F W = F ^ { 2 ( k + 1 ) } W ( G , K ) \subseteq W ( G , K ), \end{equation*} | |
| − | + | generated by $S ^ { \text{l} } ( \mathfrak { g } ^ { * } )$, for $\text{l} \geq k + 1$. This leads to the truncated Weil algebra | |
| + | |||
| + | \begin{equation*} W _ { k } = W ( G , K ) _ { k } = W ( G , K ) / F W. \end{equation*} | ||
| + | |||
| + | The cohomology $H ^ { * } ( W _ { k } )$ plays a prominent role in the study of secondary characteristic classes (cf. also [[Characteristic class|Characteristic class]]) of foliations and foliated bundles [[#References|[a3]]] (see also [[#References|[a2]]]). | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> H. Cartan, "Cohomologie réelle d'un espace fibré principal differentiable" , ''Sem. H. Cartan 1949/50, Exp. 19–20'' (1950)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J.L. Dupont, F.W. Kamber, "On a generalization of Cheeger–Chern–Simons classes" ''Illinois J. Math.'' , '''34''' (1990) {{MR|1046564}} {{ZBL|0724.57018}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> F.W. Kamber, Ph. Tondeur, "Foliated bundles and characteristic classes" , ''Lecture Notes in Mathematics'' , '''493''' , Springer (1975) {{MR|0402773}} {{MR|0385886}} {{ZBL|0311.57011}} {{ZBL|0308.57011}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> F.W. Kamber, Ph. Tondeur, "Semi-simplicial Weil algebras and characteristic classes" ''Tôhoku Math. J.'' , '''30''' (1978) pp. 373–422 {{MR|0509023}} {{ZBL|0398.57006}} </td></tr></table> |
Revision as of 16:57, 1 July 2020
Let $G$ be a connected Lie group with Lie algebra $\frak g$. The Weil algebra $W ( \mathfrak{g} )$ of $\frak g$ was first introduced in a series of seminars by H. Cartan [a1], in part based on some unpublished work of A. Weil. As a differential graded algebra, it is given by the tensor product
\begin{equation*} W ( \mathfrak { g } ) = \bigwedge \mathfrak { g } ^ { * } \bigotimes S \mathfrak { g } ^ { * }, \end{equation*}
where $\wedge \mathfrak { g } ^ { * }$ and $S \mathfrak { g } ^ { * }$ denote the exterior and symmetric algebras, respectively (cf. also Exterior algebra; Symmetric algebra).
The Weil algebra and its generalizations have been studied extensively by F.W. Kamber and Ph. Tondeur [a3] [a4]. Let $K \subseteq G$ be a maximal compact subgroup, with $\frak p$ denoting the Lie algebra of $K$. The relative Weil algebra for $( G , K )$ is defined by
\begin{equation*} W ( G , K ) = \{ \bigwedge ( \mathfrak { g } / \mathfrak { k } ) ^ { * } \bigotimes S \mathfrak { g } ^ { * } \} ^ { K }. \end{equation*}
With regards to the universal classifying bundle $E G \rightarrow B G$ (cf. also Bundle; Classifying space; Universal space), there are canonical isomorphisms in cohomology
 |
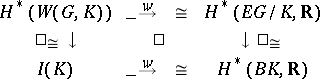where $I ( K )$ denotes the $\operatorname{Ad} K$-invariant polynomials. For a given integer 
, one has the ideal
\begin{equation*} F W = F ^ { 2 ( k + 1 ) } W ( G , K ) \subseteq W ( G , K ), \end{equation*}
generated by $S ^ { \text{l} } ( \mathfrak { g } ^ { * } )$, for $\text{l} \geq k + 1$. This leads to the truncated Weil algebra
\begin{equation*} W _ { k } = W ( G , K ) _ { k } = W ( G , K ) / F W. \end{equation*}
The cohomology $H ^ { * } ( W _ { k } )$ plays a prominent role in the study of secondary characteristic classes (cf. also Characteristic class) of foliations and foliated bundles [a3] (see also [a2]).
References
| [a1] | H. Cartan, "Cohomologie réelle d'un espace fibré principal differentiable" , Sem. H. Cartan 1949/50, Exp. 19–20 (1950) |
| [a2] | J.L. Dupont, F.W. Kamber, "On a generalization of Cheeger–Chern–Simons classes" Illinois J. Math. , 34 (1990) MR1046564 Zbl 0724.57018 |
| [a3] | F.W. Kamber, Ph. Tondeur, "Foliated bundles and characteristic classes" , Lecture Notes in Mathematics , 493 , Springer (1975) MR0402773 MR0385886 Zbl 0311.57011 Zbl 0308.57011 |
| [a4] | F.W. Kamber, Ph. Tondeur, "Semi-simplicial Weil algebras and characteristic classes" Tôhoku Math. J. , 30 (1978) pp. 373–422 MR0509023 Zbl 0398.57006 |
How to Cite This Entry:
Weil algebra of a Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil_algebra_of_a_Lie_algebra&oldid=50192
Weil algebra of a Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil_algebra_of_a_Lie_algebra&oldid=50192
This article was adapted from an original article by James F. Glazebrook (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article