Difference between revisions of "Turán theory"
Ulf Rehmann (talk | contribs) m (moved Turan theory to Turán theory over redirect: accented title) |
m (AUTOMATIC EDIT (latexlist): Replaced 240 formulas out of 251 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 251 formulas, 240 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
P. Turán introduced [[#References|[a52]]] and developed (see [[#References|[a9]]], [[#References|[a10]]], [[#References|[a11]]], [[#References|[a12]]], [[#References|[a13]]], [[#References|[a14]]], [[#References|[a16]]], [[#References|[a21]]], [[#References|[a22]]], [[#References|[a23]]], [[#References|[a24]]], [[#References|[a25]]], [[#References|[a26]]], [[#References|[a27]]], [[#References|[a28]]], [[#References|[a29]]], [[#References|[a30]]], [[#References|[a31]]], [[#References|[a32]]], [[#References|[a33]]], [[#References|[a34]]], [[#References|[a35]]], [[#References|[a36]]], [[#References|[a37]]], [[#References|[a38]]], [[#References|[a39]]], [[#References|[a40]]], [[#References|[a41]]], [[#References|[a46]]], and all papers by Turán mentioned below) the power sum method, by which one can investigate certain minimax problems described below. The method is used in many problems of analytic [[Number theory|number theory]], analysis and applied mathematics. | P. Turán introduced [[#References|[a52]]] and developed (see [[#References|[a9]]], [[#References|[a10]]], [[#References|[a11]]], [[#References|[a12]]], [[#References|[a13]]], [[#References|[a14]]], [[#References|[a16]]], [[#References|[a21]]], [[#References|[a22]]], [[#References|[a23]]], [[#References|[a24]]], [[#References|[a25]]], [[#References|[a26]]], [[#References|[a27]]], [[#References|[a28]]], [[#References|[a29]]], [[#References|[a30]]], [[#References|[a31]]], [[#References|[a32]]], [[#References|[a33]]], [[#References|[a34]]], [[#References|[a35]]], [[#References|[a36]]], [[#References|[a37]]], [[#References|[a38]]], [[#References|[a39]]], [[#References|[a40]]], [[#References|[a41]]], [[#References|[a46]]], and all papers by Turán mentioned below) the power sum method, by which one can investigate certain minimax problems described below. The method is used in many problems of analytic [[Number theory|number theory]], analysis and applied mathematics. | ||
| − | Let | + | Let $S$ be a fixed set of integers. Let $b _ { j }$ be fixed complex numbers and let $z_j$ be complex numbers from a prescribed set. Define the following norms: |
| − | Bohr norm: | + | Bohr norm: $M _ { 0 } ( k ) = \sum _ { j = 1 } ^ { n } | b _ { j } \| z _ { j } | ^ { k }$; |
| − | minimum norm: | + | minimum norm: $M _ { 1 } ( k ) = \operatorname { min } _ { j } | z _ { j } | ^ { k }$; |
| − | maximum norm: | + | maximum norm: $M _ { 2 } ( k ) = \operatorname { max } _ { j } | z _ { j } | ^ { k }$; |
| − | Wiener norm: | + | Wiener norm: $M _ { 3 } ( k ) = \left( \sum _ { j = 1 } ^ { n } | b _ { j } | ^ { 2 } | z _ { j } | ^ { 2 k } \right) ^ { 1 / 2 }$; |
| − | separation norm: | + | separation norm: $M _ { 4 } = \operatorname { min } _ { 1 \leq j < k \leq n } | z _ { j } - z _ { k } |$; |
| − | Cauchy norm: | + | Cauchy norm: $M _ { 5 } = \operatorname { max } _ { j } | b _ { j } |$; |
| − | argument norm: | + | argument norm: $M _ { 6 } = \operatorname { min } _ { j } | \operatorname { arc } z _ { j } |$. Turán's method deals with the following problems [[#References|[a91]]]. |
| − | 1) Determine, for | + | 1) Determine, for $d \in [ 0,3 ]$, |
| − | + | \begin{equation} \tag{a1} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k \in S } \frac { | \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } | } { M _ { d } ( k ) }, \end{equation} | |
| − | where the infimum is taken over all complex numbers | + | where the infimum is taken over all complex numbers $z_j$ (two-sided direct problems). |
| − | 2) Find the above minimum in (a1) over all complex numbers | + | 2) Find the above minimum in (a1) over all complex numbers $z_j$ satisfying $M _ { 4 } \geq \delta > 0$ or $M _ { 6 } \geq \kappa > 0$ ( "two-sided conditional problems" ). |
| − | 3) For a given domain | + | 3) For a given domain $U$ and $d \in [ 0,3 ]$, find |
| − | + | \begin{equation*} \operatorname { inf } _ { z _ { j } \in U } \operatorname { max } _ { k \in S } \frac { \operatorname { Re } \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } } { M _ { d } ( k ) } \end{equation*} | |
(one-sided conditional problems). | (one-sided conditional problems). | ||
| − | 4) For a given weight function | + | 4) For a given weight function $\psi ( k , n ) > 0$ and $d \in [ 0,3 ]$, find |
| − | + | \begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k \in S } \left( \frac { | \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } | \psi ( k , n ) } { M _ { d } ( k ) } \right) ^ { 1 / k } \end{equation*} | |
(weighted two-sided problems). | (weighted two-sided problems). | ||
| − | 5) For a given domain | + | 5) For a given domain $U$ and $0 \leq d \leq 3$, find |
| − | + | \begin{equation*} \operatorname { sup } _ { z _ { 1 } , \ldots , z _ { n } \in U } \operatorname { min } _ { k \in S } \frac { | \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } | } { M _ { d } ( k ) } \end{equation*} | |
(dual conditional problems). | (dual conditional problems). | ||
| − | 6) Given polynomials | + | 6) Given polynomials $\phi ( x )$ and $\phi _ { j } ( x )$, $d \in [ 0,3 ]$, $g _ { 1 } ( k ) = \sum _ { j = 1 } ^ { n } \phi _ { j } ( k ) z _ { j } ^ { k }$ and $g _ 2 ( k ) = \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } \phi ( z _ { j } )$, determine |
| − | + | \begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k \in S } \frac { | g _ { 1 } ( k ) | } { M _ { d } ( k ) } \end{equation*} | |
and | and | ||
| − | + | \begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k \in S } \frac { | g _ { 2 } ( k ) | } { M _ { d } ( k ) } \end{equation*} | |
(two-sided direct operator problems). | (two-sided direct operator problems). | ||
| − | 7) Given a domain | + | 7) Given a domain $U$ and $d \in [ 0,3 ]$, find |
| − | + | \begin{equation*} \operatorname { inf } _ { z _ { 1 } , \ldots , z _ { n } \in U } \operatorname { max } _ { k \in S } \frac { \operatorname { Re } g _ { 1 } ( k ) } { M _ { d } ( k ) } \end{equation*} | |
and | and | ||
| − | + | \begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k \in S } \frac { \operatorname { Re } g _ { 2 } ( k ) } { M _ { d } ( k ) }, \end{equation*} | |
| − | where | + | where $g _ { 1 } ( k )$ and $g_2 ( k )$ are as above (one-sided conditional operator problems). |
| − | 8) Given a finite set | + | 8) Given a finite set $S$ of integers, fixed complex numbers $b _ { j }$, $d \in [ 0,3 ]$, and two generalized power sums $g _ { 1 } ( k ) = \sum _ { j = 1 } ^ { n } b _ { j } ^ { \prime } ( k ) z _ { j } ^ { k }$, $g_2 ( k ) = \sum _ { j = 1 } ^ { n } b _ { j } ^ { \prime \prime } ( k ) z _ { j } ^ { k }$, how large can the quantities |
| − | + | \begin{equation*} \frac { | g _ { 1 } ( k ) | } { M _ { d ^ { \prime } } ( k ) } , \frac { | g _ { 2 } ( k ) | } { M _ { d ^ { \prime \prime } } ( k ) } \quad ( k \in S ) \end{equation*} | |
| − | be made simultaneously depending only on | + | be made simultaneously depending only on $b _ { j }$, $d ^ { \prime }$, $d ^ { \prime \prime }$, $n$, and $S$ (simultaneous problems)? |
| − | 9) Given two finite sets of integers | + | 9) Given two finite sets of integers $S _ { 1 }$ and $S _ { 2 }$, fixed complex numbers $b _ { j }$, $h ( m , k ) = \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } w _ { j }^ { m }$, $| z _ { 1 } | \geq \ldots \geq | z _ { n } |$, $| w _ { 1 } | \geq \ldots \geq | w _ { n } |$, and $0 \leq d ^ { \prime } , d ^ { \prime \prime } \leq 3$, what is |
| − | + | \begin{equation*} \operatorname { inf } _ { z _ { j } , w _ { j } } \operatorname { max } _ { k \in S _ { 1 } , \atop m \in S _ { 2 } } \frac { | h ( m , k ) | } { M _ { d ^ { \prime } } ( k ) M _ { d^ { \prime \prime } } ( m ) } \end{equation*} | |
and what are the extremal systems (several variables problems)? | and what are the extremal systems (several variables problems)? | ||
| Line 77: | Line 85: | ||
Turán and others obtained some lower bounds for some of the above problems. | Turán and others obtained some lower bounds for some of the above problems. | ||
| − | Let | + | Let $s _ { k } = z _ { 1 } ^ { k } + \ldots + z _ { n } ^ { k }$ be a pure power sum. Then |
| − | + | \begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k = 1 , \ldots , n } \frac { | s _ { k } | } { M _ { 1 } ( k ) } = 1 \end{equation*} | |
and | and | ||
| − | + | \begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k = 1 , \ldots , 2 n - 1 } \frac { | s _ { k } | } { M _ { 2 } ( k ) } = 1 \end{equation*} | |
| − | (see also [[#References|[a4]]]). These results were obtained in the equivalent form with | + | (see also [[#References|[a4]]]). These results were obtained in the equivalent form with $M _ { 1 } ( k ) = 1$ and $M _ { 2 } ( k ) = 1$, respectively. |
| − | Also, let | + | Also, let $R _ { n } = \operatorname { min } _ { z _ { j } } \operatorname { max } _ { k = 1 , \ldots , n } | s _ { k } |$, where $\max| z _ { j } | = 1$. Then |
| − | + | \begin{equation} \tag{a2} R _ { n } > \frac { \operatorname { log } 2 } { 1 + \frac { 1 } { 2 } + \ldots + \frac { 1 } { n } }. \end{equation} | |
| − | F.V. Atkinson [[#References|[a2]]] improved this by showing that | + | F.V. Atkinson [[#References|[a2]]] improved this by showing that $R _ { n } > 1 / 5$. A. Biro [[#References|[a3]]] proved that $R _ { n } > 1 / 2$ and that if $m > 0$ is such that $z _ { 1 } = \ldots = z _ { m } = 1$, $n \geq n _ { 0 }$, then |
| − | + | \begin{equation*} \operatorname { max } _ { j = 1 , \ldots , n - m + 1 } | s _ { j } | \geq m \left( \frac { 1 } { 2 } + \frac { m } { 8 n } + \frac { 3 m ^ { 2 } } { 64 n ^ { 2 } } \right). \end{equation*} | |
| − | J. Anderson [[#References|[a1]]] showed that if | + | J. Anderson [[#References|[a1]]] showed that if $\operatorname{min}_{j} | z _ { j } | = 1$, then $\operatorname { inf } _ { z _ { j } } \operatorname { max } _ { j = 1 , \ldots , n^2 } | s _ { j } | \geq \sqrt { n }$, and that if $n + 1$ is a [[Prime number|prime number]], then this <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120200/t12020075.png"/> lies in $[ \sqrt { n } , \sqrt { n + 1 } ]$; he also proved that if $m \in [ 1 , n - 1 ]$, then there exists a $c = c ( m )$ such that |
| − | + | \begin{equation*} \operatorname { max } _ { r = 1 , \ldots , c n } \frac { | z _ { 1 } ^ { r } + \ldots + z _ { n } ^ { r } | } { \operatorname { min } _ { k = 1 , \ldots , n } | z _ { k } ^ { r } | } \geq m. \end{equation*} | |
| − | It is also known [[#References|[a43]]] that, on the other hand, | + | It is also known [[#References|[a43]]] that, on the other hand, $R _ { n } < 1 - \operatorname { log } n / ( 3 n )$ for infinitely many $n$ and that $R _ { n } < 1 - 1 / ( 250 n )$ for large enough $n$. |
P. Erdös proved that | P. Erdös proved that | ||
| − | + | \begin{equation*} M _ { 2 } = \operatorname { min } _ { z _ { j } } \operatorname { max } _ { k = 2 , \ldots , n + 1 } | s _ { k } | \leq 2 ( n + 1 ) ^ { 2 } e ^ { - \theta n }, \end{equation*} | |
| − | where | + | where $\theta \approx 0.2784$ is the solution of the equation $x \operatorname { exp } ( x + 1 ) = 1$, and L. Erdös [[#References|[a15]]] proved that if $n$ is large enough, then $\operatorname { exp } ( - 2 \theta n - 0.7823 \operatorname { log } n ) \leq M _ { 2 } \leq \operatorname { exp } ( - 2 \theta n + 4.5 \operatorname { log } n )$, where $\theta$ is the solution of the equation $1 + \theta + \operatorname { log } \theta = 0$. |
E. Makai [[#References|[a44]]] showed that | E. Makai [[#References|[a44]]] showed that | ||
| − | + | \begin{equation*} M _ { 3 } = \operatorname { min } _ { z _ { j } } \operatorname { max } _ { k = 3 , \ldots , n + 2 } | s _ { k } | < \frac { 1 } { 1.473 ^ { n } } \text { for } n > n _ { 0 }. \end{equation*} | |
| − | For generalized power sums | + | For generalized power sums $g ( k ) = \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k }$, Turán proved that if $\min_{ z _ { j }} | z _ { j } | = 1$, then |
| − | + | \begin{equation*} \operatorname { max } _ { k = m + 1 , \ldots , m + n } | g ( k ) | \geq \left( \frac { n } { 2 e ( m + n ) } \right) ^ { n } | b _ { 1 } + \ldots + b _ { n } |. \end{equation*} | |
| − | Makai [[#References|[a45]]] and N.G. de Bruijn [[#References|[a4]]] proved, independently, that | + | Makai [[#References|[a45]]] and N.G. de Bruijn [[#References|[a4]]] proved, independently, that $( n / ( 2 e ( m + n ) ) ) ^ { n }$ can be replaced with $1 / P _ { m , n }$, where $P _ { m , n } = \sum _ { j = 0 } ^ { n - 1 } \left( \begin{array} { c } { m + j } \\ { j } \end{array} \right) 2 ^ { j }$. If, however, one replaces it with $1 / ( P _ { m ,\, n } - \epsilon )$ for any $\epsilon > 0$, then the above inequality fails. Turán also proved that if $\operatorname{min}_{j} | z _ { j } | = 1$, then |
| − | + | \begin{equation*} \operatorname { max } _ { k = m + 1 , \ldots , m + n } | g ( k ) | \geq \frac { 1 } { 3 } | g ( 0 ) | \prod _ { j = 1 } ^ { n } \frac { | z _ { j } | - \operatorname { exp } ( - 1 / m ) } { | z _ { j } | + 1 }. \end{equation*} | |
| − | G. Halasz showed that for any | + | G. Halasz showed that for any $k > 1$, |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120200/t120200103.png"/></td> </tr></table> |
| − | S. Gonek [[#References|[a18]]] proved that for all | + | S. Gonek [[#References|[a18]]] proved that for all $r > 0$, |
| − | + | \begin{equation*} \operatorname { max } _ { 1 \leq k \leq 4 \left( \begin{array} { c } { n + r - 1 } \\ { r } \end{array} \right)} | g ( k ) | \geq | g ( 0 ) | \left( 2 e \left( \begin{array} { c } { n + r - 1 } \\ { r } \end{array} \right) \right) ^ { - 1 / r }. \end{equation*} | |
| − | In the case of the maximum norm, V. Sos and Turán [[#References|[a46]]] obtained the following result. Let | + | In the case of the maximum norm, V. Sos and Turán [[#References|[a46]]] obtained the following result. Let $1 = | z _ { 1 } | \geq \ldots \geq | z _ { n } |$. Then for any integer $m \geq 0$, |
| − | + | \begin{equation*} \operatorname { max } _ { k = m + 1 , \ldots , m + n } | g ( k ) | \geq c _ { m , n } , \operatorname { min } _ { j = 1 , \ldots , n } | b _ { 1 } + \ldots + b _ { j } | \end{equation*} | |
| − | with | + | with $c _ { m , n } = 2 ( n / ( 8 e ( m + n ) ) ) ^ { n }$. G. Kolesnik and E.G. Straus [[#References|[a42]]] improved this by showing that one can take $c _ { m , n } = \sqrt { n } ( n / ( 4 e ( m + n ) ) ) ^ { n }$. On the other hand, Makai [[#References|[a45]]] showed that for |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120200/t120200111.png"/></td> </tr></table> |
| − | the inequality fails for some | + | the inequality fails for some $m$ and $z_j$. |
| − | Considering different ranges for | + | Considering different ranges for $k$, Halasz [[#References|[a19]]] proved that if $m , n < N$, then |
| − | + | \begin{equation*} \operatorname { min } _ { k = m + 1 , \ldots , m + N } | g ( k ) | \geq \end{equation*} | |
| − | + | \begin{equation*} \geq \frac { n } { 4 N ^ { 3 / 2} } \operatorname { exp } \left( - 30 n \left( \frac { 1 } { \operatorname { log } ( N / n ) } + \frac { 1 } { \operatorname { log } ( N / m ) } \right) \right) \times \times \operatorname { min } _ { l \leq n } \left| \sum _ { j = 1 } ^ { l } b _ { j }\right| . \end{equation*} | |
==Other norms and conditions.== | ==Other norms and conditions.== | ||
The following results are obtained for two-sided problems with other norms and conditions. | The following results are obtained for two-sided problems with other norms and conditions. | ||
| − | A) ([[#References|[a17]]], [[#References|[a47]]], [[#References|[a8]]], [[#References|[a45]]]). Let | + | A) ([[#References|[a17]]], [[#References|[a47]]], [[#References|[a8]]], [[#References|[a45]]]). Let $z_j$ be ordered so that $0 = | z _ { 1 } - 1 | \leq \ldots \leq | z _ { n } - 1 |$. Assume that $m \geq - 1$ and $n > 1$. Then |
| − | + | \begin{equation*} \operatorname { max } _ { k = m + 1 , \ldots , m + n } | g ( k ) | \geq \end{equation*} | |
| − | + | \begin{equation*} \geq \frac { 1 } { 8 } \left( \frac { n - 1 } { 8 e ( m + n ) } \right) ^ { n } \operatorname { min }_ j | b _ { 1 } + \ldots + b _ { j } |. \end{equation*} | |
| − | B) ([[#References|[a91]]]). Let | + | B) ([[#References|[a91]]]). Let $z_j$ be ordered as in A). Assume that $m > - 1$ and $0 < \delta _ { 1 } < \delta _ { 2 } < n / ( m + n + 1 )$, let $h$ be the largest integer satisfying $| 1 - z _ { h } | < \delta _ { 1 }$ and let $l$ be the smallest integer satisfying $| 1 - z _{l + 1} | > \delta _ { 2 }$ (if such an integer does not exist, take $l = n$). Then |
| − | + | \begin{equation*} \operatorname { max } _ { k = m + 1 , \ldots , m + n } | g ( k ) | \geq \end{equation*} | |
| − | + | \begin{equation*} \geq 2 \left( \frac { \delta _ { 1 } - \delta _ { 2 } } { 12 e } \right) ^ { n } \operatorname { min } _ { j = h , \ldots , l } | b _ { 1 } + \ldots + b _ { j } |. \end{equation*} | |
| − | C) ([[#References|[a12]]]). Let | + | C) ([[#References|[a12]]]). Let $m \geq 0$ and let $k$, $k_{1}$, $k_2$ be such that |
| − | + | \begin{equation*} | z _ { 1 } | \geq \ldots \geq | z _ { k _ { 1 } } | > \frac { m + 2 n } { m + n } \geq \end{equation*} | |
| − | + | \begin{equation*} \geq | z _ { k_1 } + 1 | \geq \ldots \geq | z _ { k } | = 1 \geq \ldots \geq | z _ { k _ { 2 } } - 1 | > > \frac { m } { m + n } \geq | z _ { k _ { 2 } } | \geq \ldots \geq | z _ { n } |. \end{equation*} | |
Then | Then | ||
| − | + | \begin{equation*} \operatorname { max } _ { r = m + 1 , \ldots , m + n } | g ( r ) | \geq \end{equation*} | |
| − | + | \begin{equation*} \geq \frac { 1 } { n } \left( \frac { n } { 16 e ( m + n ) } \right) ^ { n } \times \times \operatorname{min} _ { k _ { 1 } \leq l _ { 1 } \leq k \leq l _ { 2 } \leq k _ { 2 } } | b _ {l_{ 1} } + \ldots + b _ {l_{ 2 }} |. \end{equation*} | |
| − | D) ([[#References|[a59]]]). If | + | D) ([[#References|[a59]]]). If $m > - 1$ and $\operatorname {min}_{ \mu \neq \nu} | z _ { \mu } - z _ { \nu } | \geq \delta \operatorname { max } _ { j } | z _ { j }|$, then |
| − | + | \begin{equation*} \frac { \max_{k = m + 1 , \ldots , m + n}| g ( k ) | } { \sum _ { j = 1 } ^ { n } | b _ { j } z _ { j } ^ { k } | } \geq \frac { 1 } { n } ( \frac { \delta } { 2 } ) ^ { n - 1 }. \end{equation*} | |
| − | E) ([[#References|[a8]]]). If | + | E) ([[#References|[a8]]]). If $m > - 1$ and $r$ is such that $\operatorname{min}_{j \neq r} | z _ { j } - z _ { r } | \geq \delta | z _ { r } |$, then there exists a $ k \in [ m + 1 , m + n ]$ such that |
| − | + | \begin{equation*} | g ( k ) | \geq ( \frac { \delta } { 2 + 2 \delta } ) ^ { n - 1 } | b _ { r } z _ { r} ^ { k } |. \end{equation*} | |
| − | F) ((Halasz). Let | + | F) ((Halasz). Let $m_1$ and $m _ { 2 }$ be non-negative integers, $m = \operatorname { max } ( m _ { 1 } , m _ { 2 } )$, and $S = [ - m _ { 1 } - n , - m _ { 1 } - 1 ] \cup [ m _ { 2 } + 1 , m _ { 2 } + n ]$. Assume that $z _ { 1 } \dots z _ { n } \neq 0$. Then there exists an integer $k \in S$ such that |
| − | + | \begin{equation*} | g ( k ) | \geq \left( \frac { n } { 8 e ( m + n ) } \right) ^ { n } | g ( 0 ) |. \end{equation*} | |
| − | G) (Turán). If | + | G) (Turán). If $S = [ m + 1 , m + n ] \cup [ 2 m + 1,2 m + n ]$, then the above inequality holds with $6$ instead of $8$. |
==Problems of type 3) and 7).== | ==Problems of type 3) and 7).== | ||
| − | Assume that | + | Assume that $\kappa \leq | \operatorname { arc } z _ { j } | \leq \pi$, $j = 1 , \ldots , n$, with $0 < \kappa \leq \pi / 2$, let $a _ { j }$ be real numbers, and let $\phi ( z ) = z ^ { k } + a _ { 1 } z ^ { k - 1 } + \ldots + a _ { k } \neq 0$ for $| z | > \rho \in ( 0,1 )$. Define $G _ { 2 } ( k ) = \sum _ { j = 1 } ^ { n } b _ { j } \phi ( z _ { j } ) z _ { j } ^ { k }$ for some fixed complex numbers $b _ { j }$. Assuming that $\operatorname{min}_{j} | z _ { j } | = 1$, Turán proved that $\max _ r \operatorname { Re } G _ { 2 } ( r ) \geq A$ and $\operatorname { min}_r \operatorname { Re } G _ { 2 } ( r ) \leq - A$, where |
| − | + | \begin{equation*} A = \frac { 1 } { 6 n 16 ^ { n } } \left( \frac { 1 + \rho } { 2 } \right) ^ { m } \left( \frac { 1 - \rho } { 2 } \right) ^ { 2 n + k } \left| \operatorname { Re } \sum _ { j = 1 } ^ { n } b _ { j } \right| \end{equation*} | |
| − | and the minimum is taken over all integers | + | and the minimum is taken over all integers $r \in [ m + 1 , m + n ( 3 + \pi / k ) ]$. |
| − | If | + | If $\phi ( z ) = 1$, then the above inequalities hold with |
| − | + | \begin{equation*} A = \frac { 1 } { 6 n } \operatorname { min } _ { n \leq x \leq 2 n } \left( \frac { x } { 4 e ( m + x ) } \right) ^ { x } \left| \operatorname { Re } \sum _ { j = 1 } ^ { n } b _ { j } \right|. \end{equation*} | |
| − | Also, if | + | Also, if $P _ { j } ( x )$ are polynomials of degree $k_j - 1$, $G _ { 1 } ( r ) = \sum _ { j = 1 } ^ { n } P _ { j } ( r ) z _ { j } ^ { r }$ and $K = k _ { 1 } + \ldots + k _ { n }$, then $\operatorname {max}_{r}\operatorname { Re } G _ { 1 } ( r ) \geq B$ and $\min_r \operatorname{Re} G _ { 1 } ( r ) \leq - B$, where |
| − | + | \begin{equation*} B = \frac { 1 } { 6 K } \left( \frac { K } { 4 e ( m + 2 K ) } \right) ^ { 2 K } \left| \operatorname { Re } \sum _ { j = 0 } ^ { n } P _ { j } ( 0 ) \right| \end{equation*} | |
| − | and the range of | + | and the range of $r$ is $[ m + 1 , m + K ( 3 + \pi / \kappa ) ]$. |
| − | Assume now that | + | Assume now that $\operatorname {max}_{j} | z _ { j } | = 1$. Let $G _ { 2 } ( r )$ be as defined above, and assume $\phi ( z ) \neq 0$ for $z \in \{ | z | \geq \rho \} \cup \{ | \operatorname { arc } z | < \kappa \}$, where $0 < \rho < 1$ and $0 < \kappa < \pi / 2$. Assume also that $\kappa \leq | \operatorname { arc } z _ { j } | < \pi$, $j = 1 , \ldots , n$. Take any $\delta _ { 1 }$, $\delta _ { 2 }$ satisfying $1 > \delta _ { 1 } > \delta _ { 2 } \geq \rho$ and define $h_{1}$, $h _ { 2 }$ by |
| − | + | \begin{equation*} 1 = | z _ { 1 } | \geq \ldots \geq | z _ { h _ { 1 } } | \geq \delta _ { 1 } > \end{equation*} | |
| − | + | \begin{equation*} > | z _ { h _ { 1 } } + 1 | \geq \ldots \geq | z _ { h _ { 2 } } | > \delta _ { 2 } \geq \end{equation*} | |
| − | + | \begin{equation*} \geq | z _ { h_2 } + 1 | \geq \ldots \geq | z _ { n } |. \end{equation*} | |
| − | (If | + | (If $h_{1}$ or $h _ { 2 }$ do not exist, replace them with $n$.) Put $I = [ m + 1 , m + ( n + k ) ( 3 + \pi / k ) ]$ and |
| − | + | \begin{equation*} M = \frac { 1 } { 3 ( n + k ) } \left( \frac { \delta _ { 1 } - \delta _ { 2 } } { 16 } \right) ^ { 2 n + 2 k } \delta _ { 2 } ^ { m + ( n + k ) ( 1 + \pi / k ) }\times \end{equation*} | |
| − | + | \begin{equation*} \times \operatorname { min } _ { h _ { 1 } \leq j \leq h _ { 2 } } | \operatorname { Re } ( b _ { 1 } + \ldots + b _ { j } ) |. \end{equation*} | |
| − | Then | + | Then $\max_{r \in I} \text{Re} \, G_2 (r ) \geq M$ and $\operatorname{min}_{r\in I} \operatorname{Re} G _ { 2 } ( r ) \leq - M$. If $\phi ( z ) = 1$, then the above result holds with $k = \rho = 0$. |
| − | J.D. Buchholtz [[#References|[a5]]], [[#References|[a6]]] proved that if | + | J.D. Buchholtz [[#References|[a5]]], [[#References|[a6]]] proved that if $\operatorname {max}_{j} | z _ { j } | = 1$, then |
| − | + | \begin{equation*} \operatorname { max } _ { k = 1 , \ldots , n } \left( \frac { 1 } { n } | s _ { k } | \right) ^ { 1 / k } > \frac { 1 } { 5 } > \frac { 1 } { 2 + \sqrt { 8 } }, \end{equation*} | |
respectively, where the last result is the best possible. | respectively, where the last result is the best possible. | ||
| Line 225: | Line 233: | ||
R. Tijdeman [[#References|[a47]]] proved the following result for "operator-type problems" . | R. Tijdeman [[#References|[a47]]] proved the following result for "operator-type problems" . | ||
| − | Let | + | Let $P _ { j } ( x )$ be fixed complex polynomials of degree $k_j - 1$ and let $G _ { 1 } ( k ) = \sum _ { j = 1 } ^ { n } P _ { j } ( k ) z _ { j } ^ { k }$. Then for every integer $m \geq 0$, $K = k _ { 1 } + \ldots + k _ { n }$, and $\operatorname{min}_{j} | z _ { j } | = 1$, the inequality |
| − | + | \begin{equation} \tag{a3} \operatorname { min } _ { r = m + 1 , \ldots , m + K } | G _ { 1 } ( r ) | \geq \frac { 1 } { P _ { m , K } } \left| \sum _ { j = 1 } ^ { n } P _ { j } ( 0 ) \right| \end{equation} | |
| − | holds, where | + | holds, where $P _ { m , K }$ is defined above and the factor $1 / P _ { m , K}$ is the best possible; also, if $\operatorname {max}_{j} | z _ { j } | = 1$, then (a3) holds with $( K / ( 8 e ( m + K ) ) ) ^ { K }$ instead of $1 / P _ { m , K}$. |
J. Geysel [[#References|[a17]]] improved the above constant to | J. Geysel [[#References|[a17]]] improved the above constant to | ||
| − | + | \begin{equation*} \frac { 1 } { 4 } \left( \frac { K - 1 } { 8 e ( m + K ) } \right) ^ { K }. \end{equation*} | |
| − | Turán studied the other "operator-type problem" for | + | Turán studied the other "operator-type problem" for $G _ { 2 } ( r ) = \sum _ { j = 1 } ^ { n } b _ { j } \phi ( z _ { j } ) z _ { j } ^ { k }$. Let $b _ { j }$ be fixed complex numbers and let $\phi ( z ) = z ^ { k } + a _ { 1 } z ^ { k - 1 } + \ldots + a _ { k }$ be a polynomial with no zeros outside $| z | < \rho$. Assume that $m > - 1$, $0 < \rho < 1$ and $\operatorname {max}_{j} | z _ { j } | = 1$. Then |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120200/t120200232.png"/></td> <td style="width:5%;text-align:right;" valign="top">(a4)</td></tr></table> |
with | with | ||
| − | + | \begin{equation*} c _ { m , n } = 2 ^ { - n } \left( \frac { 1 + \rho } { 2 } \right) ^ { m } \left( \frac { 1 - \rho } { 2 } \right) ^ { n + k }. \end{equation*} | |
| − | In case of the maximum norm and | + | In case of the maximum norm and $1 = | z _ { 1 } | \geq \ldots \geq | z _ { n } | > 0$, Turán proved (a4) with |
| − | + | \begin{equation*} c _ { m ,\, n } = \left\{ \begin{array} { l l } { 2 ^ { 1 - n } \left( \frac { n + k } { 4 e ( m + n + k ) } \right) ^ { n + k } } & { \text { if } \frac { m } { m + n + k } \geq \rho, } \\ { \rho ^ { m } 2 ^ { 1 - n } \left( \frac { 1 - \rho } { 4 } \right) ^ { n + k } } & { \text { if } \frac { m } { m + n + k } < \rho. } \end{array} \right. \end{equation*} | |
| − | He also proved the following "simultaneous problem" . Let | + | He also proved the following "simultaneous problem" . Let $\operatorname{min}_j | z _ { j } | = \operatorname { min } _ { j } | w _ { j } | = 1$. For any integers $m > - 1$ and $n _ { 1 } , n _ { 2 } \geq 1$ there exist a $ k \in [ m + 1 , m + n _ { 1 } n _ { 2 } ]$ such that the inequalities |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120200/t120200240.png"/></td> </tr></table> |
and | and | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120200/t120200241.png"/></td> </tr></table> |
hold simultaneously. | hold simultaneously. | ||
====References==== | ====References==== | ||
| − | + | < | |
Revision as of 16:46, 1 July 2020
P. Turán introduced [a52] and developed (see [a9], [a10], [a11], [a12], [a13], [a14], [a16], [a21], [a22], [a23], [a24], [a25], [a26], [a27], [a28], [a29], [a30], [a31], [a32], [a33], [a34], [a35], [a36], [a37], [a38], [a39], [a40], [a41], [a46], and all papers by Turán mentioned below) the power sum method, by which one can investigate certain minimax problems described below. The method is used in many problems of analytic number theory, analysis and applied mathematics.
Let $S$ be a fixed set of integers. Let $b _ { j }$ be fixed complex numbers and let $z_j$ be complex numbers from a prescribed set. Define the following norms:
Bohr norm: $M _ { 0 } ( k ) = \sum _ { j = 1 } ^ { n } | b _ { j } \| z _ { j } | ^ { k }$;
minimum norm: $M _ { 1 } ( k ) = \operatorname { min } _ { j } | z _ { j } | ^ { k }$;
maximum norm: $M _ { 2 } ( k ) = \operatorname { max } _ { j } | z _ { j } | ^ { k }$;
Wiener norm: $M _ { 3 } ( k ) = \left( \sum _ { j = 1 } ^ { n } | b _ { j } | ^ { 2 } | z _ { j } | ^ { 2 k } \right) ^ { 1 / 2 }$;
separation norm: $M _ { 4 } = \operatorname { min } _ { 1 \leq j < k \leq n } | z _ { j } - z _ { k } |$;
Cauchy norm: $M _ { 5 } = \operatorname { max } _ { j } | b _ { j } |$;
argument norm: $M _ { 6 } = \operatorname { min } _ { j } | \operatorname { arc } z _ { j } |$. Turán's method deals with the following problems [a91].
1) Determine, for $d \in [ 0,3 ]$,
\begin{equation} \tag{a1} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k \in S } \frac { | \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } | } { M _ { d } ( k ) }, \end{equation}
where the infimum is taken over all complex numbers $z_j$ (two-sided direct problems).
2) Find the above minimum in (a1) over all complex numbers $z_j$ satisfying $M _ { 4 } \geq \delta > 0$ or $M _ { 6 } \geq \kappa > 0$ ( "two-sided conditional problems" ).
3) For a given domain $U$ and $d \in [ 0,3 ]$, find
\begin{equation*} \operatorname { inf } _ { z _ { j } \in U } \operatorname { max } _ { k \in S } \frac { \operatorname { Re } \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } } { M _ { d } ( k ) } \end{equation*}
(one-sided conditional problems).
4) For a given weight function $\psi ( k , n ) > 0$ and $d \in [ 0,3 ]$, find
\begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k \in S } \left( \frac { | \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } | \psi ( k , n ) } { M _ { d } ( k ) } \right) ^ { 1 / k } \end{equation*}
(weighted two-sided problems).
5) For a given domain $U$ and $0 \leq d \leq 3$, find
\begin{equation*} \operatorname { sup } _ { z _ { 1 } , \ldots , z _ { n } \in U } \operatorname { min } _ { k \in S } \frac { | \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } | } { M _ { d } ( k ) } \end{equation*}
(dual conditional problems).
6) Given polynomials $\phi ( x )$ and $\phi _ { j } ( x )$, $d \in [ 0,3 ]$, $g _ { 1 } ( k ) = \sum _ { j = 1 } ^ { n } \phi _ { j } ( k ) z _ { j } ^ { k }$ and $g _ 2 ( k ) = \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } \phi ( z _ { j } )$, determine
\begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k \in S } \frac { | g _ { 1 } ( k ) | } { M _ { d } ( k ) } \end{equation*}
and
\begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k \in S } \frac { | g _ { 2 } ( k ) | } { M _ { d } ( k ) } \end{equation*}
(two-sided direct operator problems).
7) Given a domain $U$ and $d \in [ 0,3 ]$, find
\begin{equation*} \operatorname { inf } _ { z _ { 1 } , \ldots , z _ { n } \in U } \operatorname { max } _ { k \in S } \frac { \operatorname { Re } g _ { 1 } ( k ) } { M _ { d } ( k ) } \end{equation*}
and
\begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k \in S } \frac { \operatorname { Re } g _ { 2 } ( k ) } { M _ { d } ( k ) }, \end{equation*}
where $g _ { 1 } ( k )$ and $g_2 ( k )$ are as above (one-sided conditional operator problems).
8) Given a finite set $S$ of integers, fixed complex numbers $b _ { j }$, $d \in [ 0,3 ]$, and two generalized power sums $g _ { 1 } ( k ) = \sum _ { j = 1 } ^ { n } b _ { j } ^ { \prime } ( k ) z _ { j } ^ { k }$, $g_2 ( k ) = \sum _ { j = 1 } ^ { n } b _ { j } ^ { \prime \prime } ( k ) z _ { j } ^ { k }$, how large can the quantities
\begin{equation*} \frac { | g _ { 1 } ( k ) | } { M _ { d ^ { \prime } } ( k ) } , \frac { | g _ { 2 } ( k ) | } { M _ { d ^ { \prime \prime } } ( k ) } \quad ( k \in S ) \end{equation*}
be made simultaneously depending only on $b _ { j }$, $d ^ { \prime }$, $d ^ { \prime \prime }$, $n$, and $S$ (simultaneous problems)?
9) Given two finite sets of integers $S _ { 1 }$ and $S _ { 2 }$, fixed complex numbers $b _ { j }$, $h ( m , k ) = \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k } w _ { j }^ { m }$, $| z _ { 1 } | \geq \ldots \geq | z _ { n } |$, $| w _ { 1 } | \geq \ldots \geq | w _ { n } |$, and $0 \leq d ^ { \prime } , d ^ { \prime \prime } \leq 3$, what is
\begin{equation*} \operatorname { inf } _ { z _ { j } , w _ { j } } \operatorname { max } _ { k \in S _ { 1 } , \atop m \in S _ { 2 } } \frac { | h ( m , k ) | } { M _ { d ^ { \prime } } ( k ) M _ { d^ { \prime \prime } } ( m ) } \end{equation*}
and what are the extremal systems (several variables problems)?
Turán and others obtained some lower bounds for some of the above problems.
Let $s _ { k } = z _ { 1 } ^ { k } + \ldots + z _ { n } ^ { k }$ be a pure power sum. Then
\begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k = 1 , \ldots , n } \frac { | s _ { k } | } { M _ { 1 } ( k ) } = 1 \end{equation*}
and
\begin{equation*} \operatorname { inf } _ { z _ { j } } \operatorname { max } _ { k = 1 , \ldots , 2 n - 1 } \frac { | s _ { k } | } { M _ { 2 } ( k ) } = 1 \end{equation*}
(see also [a4]). These results were obtained in the equivalent form with $M _ { 1 } ( k ) = 1$ and $M _ { 2 } ( k ) = 1$, respectively.
Also, let $R _ { n } = \operatorname { min } _ { z _ { j } } \operatorname { max } _ { k = 1 , \ldots , n } | s _ { k } |$, where $\max| z _ { j } | = 1$. Then
\begin{equation} \tag{a2} R _ { n } > \frac { \operatorname { log } 2 } { 1 + \frac { 1 } { 2 } + \ldots + \frac { 1 } { n } }. \end{equation}
F.V. Atkinson [a2] improved this by showing that $R _ { n } > 1 / 5$. A. Biro [a3] proved that $R _ { n } > 1 / 2$ and that if $m > 0$ is such that $z _ { 1 } = \ldots = z _ { m } = 1$, $n \geq n _ { 0 }$, then
\begin{equation*} \operatorname { max } _ { j = 1 , \ldots , n - m + 1 } | s _ { j } | \geq m \left( \frac { 1 } { 2 } + \frac { m } { 8 n } + \frac { 3 m ^ { 2 } } { 64 n ^ { 2 } } \right). \end{equation*}
J. Anderson [a1] showed that if $\operatorname{min}_{j} | z _ { j } | = 1$, then $\operatorname { inf } _ { z _ { j } } \operatorname { max } _ { j = 1 , \ldots , n^2 } | s _ { j } | \geq \sqrt { n }$, and that if $n + 1$ is a prime number, then this  lies in $[ \sqrt { n } , \sqrt { n + 1 } ]$; he also proved that if $m \in [ 1 , n - 1 ]$, then there exists a $c = c ( m )$ such that
lies in $[ \sqrt { n } , \sqrt { n + 1 } ]$; he also proved that if $m \in [ 1 , n - 1 ]$, then there exists a $c = c ( m )$ such that
\begin{equation*} \operatorname { max } _ { r = 1 , \ldots , c n } \frac { | z _ { 1 } ^ { r } + \ldots + z _ { n } ^ { r } | } { \operatorname { min } _ { k = 1 , \ldots , n } | z _ { k } ^ { r } | } \geq m. \end{equation*}
It is also known [a43] that, on the other hand, $R _ { n } < 1 - \operatorname { log } n / ( 3 n )$ for infinitely many $n$ and that $R _ { n } < 1 - 1 / ( 250 n )$ for large enough $n$.
P. Erdös proved that
\begin{equation*} M _ { 2 } = \operatorname { min } _ { z _ { j } } \operatorname { max } _ { k = 2 , \ldots , n + 1 } | s _ { k } | \leq 2 ( n + 1 ) ^ { 2 } e ^ { - \theta n }, \end{equation*}
where $\theta \approx 0.2784$ is the solution of the equation $x \operatorname { exp } ( x + 1 ) = 1$, and L. Erdös [a15] proved that if $n$ is large enough, then $\operatorname { exp } ( - 2 \theta n - 0.7823 \operatorname { log } n ) \leq M _ { 2 } \leq \operatorname { exp } ( - 2 \theta n + 4.5 \operatorname { log } n )$, where $\theta$ is the solution of the equation $1 + \theta + \operatorname { log } \theta = 0$.
E. Makai [a44] showed that
\begin{equation*} M _ { 3 } = \operatorname { min } _ { z _ { j } } \operatorname { max } _ { k = 3 , \ldots , n + 2 } | s _ { k } | < \frac { 1 } { 1.473 ^ { n } } \text { for } n > n _ { 0 }. \end{equation*}
For generalized power sums $g ( k ) = \sum _ { j = 1 } ^ { n } b _ { j } z _ { j } ^ { k }$, Turán proved that if $\min_{ z _ { j }} | z _ { j } | = 1$, then
\begin{equation*} \operatorname { max } _ { k = m + 1 , \ldots , m + n } | g ( k ) | \geq \left( \frac { n } { 2 e ( m + n ) } \right) ^ { n } | b _ { 1 } + \ldots + b _ { n } |. \end{equation*}
Makai [a45] and N.G. de Bruijn [a4] proved, independently, that $( n / ( 2 e ( m + n ) ) ) ^ { n }$ can be replaced with $1 / P _ { m , n }$, where $P _ { m , n } = \sum _ { j = 0 } ^ { n - 1 } \left( \begin{array} { c } { m + j } \\ { j } \end{array} \right) 2 ^ { j }$. If, however, one replaces it with $1 / ( P _ { m ,\, n } - \epsilon )$ for any $\epsilon > 0$, then the above inequality fails. Turán also proved that if $\operatorname{min}_{j} | z _ { j } | = 1$, then
\begin{equation*} \operatorname { max } _ { k = m + 1 , \ldots , m + n } | g ( k ) | \geq \frac { 1 } { 3 } | g ( 0 ) | \prod _ { j = 1 } ^ { n } \frac { | z _ { j } | - \operatorname { exp } ( - 1 / m ) } { | z _ { j } | + 1 }. \end{equation*}
G. Halasz showed that for any $k > 1$,
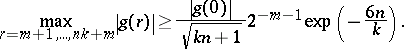 |
S. Gonek [a18] proved that for all $r > 0$,
\begin{equation*} \operatorname { max } _ { 1 \leq k \leq 4 \left( \begin{array} { c } { n + r - 1 } \\ { r } \end{array} \right)} | g ( k ) | \geq | g ( 0 ) | \left( 2 e \left( \begin{array} { c } { n + r - 1 } \\ { r } \end{array} \right) \right) ^ { - 1 / r }. \end{equation*}
In the case of the maximum norm, V. Sos and Turán [a46] obtained the following result. Let $1 = | z _ { 1 } | \geq \ldots \geq | z _ { n } |$. Then for any integer $m \geq 0$,
\begin{equation*} \operatorname { max } _ { k = m + 1 , \ldots , m + n } | g ( k ) | \geq c _ { m , n } , \operatorname { min } _ { j = 1 , \ldots , n } | b _ { 1 } + \ldots + b _ { j } | \end{equation*}
with $c _ { m , n } = 2 ( n / ( 8 e ( m + n ) ) ) ^ { n }$. G. Kolesnik and E.G. Straus [a42] improved this by showing that one can take $c _ { m , n } = \sqrt { n } ( n / ( 4 e ( m + n ) ) ) ^ { n }$. On the other hand, Makai [a45] showed that for
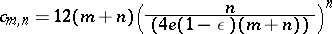 |
the inequality fails for some $m$ and $z_j$.
Considering different ranges for $k$, Halasz [a19] proved that if $m , n < N$, then
\begin{equation*} \operatorname { min } _ { k = m + 1 , \ldots , m + N } | g ( k ) | \geq \end{equation*}
\begin{equation*} \geq \frac { n } { 4 N ^ { 3 / 2} } \operatorname { exp } \left( - 30 n \left( \frac { 1 } { \operatorname { log } ( N / n ) } + \frac { 1 } { \operatorname { log } ( N / m ) } \right) \right) \times \times \operatorname { min } _ { l \leq n } \left| \sum _ { j = 1 } ^ { l } b _ { j }\right| . \end{equation*}
Other norms and conditions.
The following results are obtained for two-sided problems with other norms and conditions.
A) ([a17], [a47], [a8], [a45]). Let $z_j$ be ordered so that $0 = | z _ { 1 } - 1 | \leq \ldots \leq | z _ { n } - 1 |$. Assume that $m \geq - 1$ and $n > 1$. Then
\begin{equation*} \operatorname { max } _ { k = m + 1 , \ldots , m + n } | g ( k ) | \geq \end{equation*}
\begin{equation*} \geq \frac { 1 } { 8 } \left( \frac { n - 1 } { 8 e ( m + n ) } \right) ^ { n } \operatorname { min }_ j | b _ { 1 } + \ldots + b _ { j } |. \end{equation*}
B) ([a91]). Let $z_j$ be ordered as in A). Assume that $m > - 1$ and $0 < \delta _ { 1 } < \delta _ { 2 } < n / ( m + n + 1 )$, let $h$ be the largest integer satisfying $| 1 - z _ { h } | < \delta _ { 1 }$ and let $l$ be the smallest integer satisfying $| 1 - z _{l + 1} | > \delta _ { 2 }$ (if such an integer does not exist, take $l = n$). Then
\begin{equation*} \operatorname { max } _ { k = m + 1 , \ldots , m + n } | g ( k ) | \geq \end{equation*}
\begin{equation*} \geq 2 \left( \frac { \delta _ { 1 } - \delta _ { 2 } } { 12 e } \right) ^ { n } \operatorname { min } _ { j = h , \ldots , l } | b _ { 1 } + \ldots + b _ { j } |. \end{equation*}
C) ([a12]). Let $m \geq 0$ and let $k$, $k_{1}$, $k_2$ be such that
\begin{equation*} | z _ { 1 } | \geq \ldots \geq | z _ { k _ { 1 } } | > \frac { m + 2 n } { m + n } \geq \end{equation*}
\begin{equation*} \geq | z _ { k_1 } + 1 | \geq \ldots \geq | z _ { k } | = 1 \geq \ldots \geq | z _ { k _ { 2 } } - 1 | > > \frac { m } { m + n } \geq | z _ { k _ { 2 } } | \geq \ldots \geq | z _ { n } |. \end{equation*}
Then
\begin{equation*} \operatorname { max } _ { r = m + 1 , \ldots , m + n } | g ( r ) | \geq \end{equation*}
\begin{equation*} \geq \frac { 1 } { n } \left( \frac { n } { 16 e ( m + n ) } \right) ^ { n } \times \times \operatorname{min} _ { k _ { 1 } \leq l _ { 1 } \leq k \leq l _ { 2 } \leq k _ { 2 } } | b _ {l_{ 1} } + \ldots + b _ {l_{ 2 }} |. \end{equation*}
D) ([a59]). If $m > - 1$ and $\operatorname {min}_{ \mu \neq \nu} | z _ { \mu } - z _ { \nu } | \geq \delta \operatorname { max } _ { j } | z _ { j }|$, then
\begin{equation*} \frac { \max_{k = m + 1 , \ldots , m + n}| g ( k ) | } { \sum _ { j = 1 } ^ { n } | b _ { j } z _ { j } ^ { k } | } \geq \frac { 1 } { n } ( \frac { \delta } { 2 } ) ^ { n - 1 }. \end{equation*}
E) ([a8]). If $m > - 1$ and $r$ is such that $\operatorname{min}_{j \neq r} | z _ { j } - z _ { r } | \geq \delta | z _ { r } |$, then there exists a $ k \in [ m + 1 , m + n ]$ such that
\begin{equation*} | g ( k ) | \geq ( \frac { \delta } { 2 + 2 \delta } ) ^ { n - 1 } | b _ { r } z _ { r} ^ { k } |. \end{equation*}
F) ((Halasz). Let $m_1$ and $m _ { 2 }$ be non-negative integers, $m = \operatorname { max } ( m _ { 1 } , m _ { 2 } )$, and $S = [ - m _ { 1 } - n , - m _ { 1 } - 1 ] \cup [ m _ { 2 } + 1 , m _ { 2 } + n ]$. Assume that $z _ { 1 } \dots z _ { n } \neq 0$. Then there exists an integer $k \in S$ such that
\begin{equation*} | g ( k ) | \geq \left( \frac { n } { 8 e ( m + n ) } \right) ^ { n } | g ( 0 ) |. \end{equation*}
G) (Turán). If $S = [ m + 1 , m + n ] \cup [ 2 m + 1,2 m + n ]$, then the above inequality holds with $6$ instead of $8$.
Problems of type 3) and 7).
Assume that $\kappa \leq | \operatorname { arc } z _ { j } | \leq \pi$, $j = 1 , \ldots , n$, with $0 < \kappa \leq \pi / 2$, let $a _ { j }$ be real numbers, and let $\phi ( z ) = z ^ { k } + a _ { 1 } z ^ { k - 1 } + \ldots + a _ { k } \neq 0$ for $| z | > \rho \in ( 0,1 )$. Define $G _ { 2 } ( k ) = \sum _ { j = 1 } ^ { n } b _ { j } \phi ( z _ { j } ) z _ { j } ^ { k }$ for some fixed complex numbers $b _ { j }$. Assuming that $\operatorname{min}_{j} | z _ { j } | = 1$, Turán proved that $\max _ r \operatorname { Re } G _ { 2 } ( r ) \geq A$ and $\operatorname { min}_r \operatorname { Re } G _ { 2 } ( r ) \leq - A$, where
\begin{equation*} A = \frac { 1 } { 6 n 16 ^ { n } } \left( \frac { 1 + \rho } { 2 } \right) ^ { m } \left( \frac { 1 - \rho } { 2 } \right) ^ { 2 n + k } \left| \operatorname { Re } \sum _ { j = 1 } ^ { n } b _ { j } \right| \end{equation*}
and the minimum is taken over all integers $r \in [ m + 1 , m + n ( 3 + \pi / k ) ]$.
If $\phi ( z ) = 1$, then the above inequalities hold with
\begin{equation*} A = \frac { 1 } { 6 n } \operatorname { min } _ { n \leq x \leq 2 n } \left( \frac { x } { 4 e ( m + x ) } \right) ^ { x } \left| \operatorname { Re } \sum _ { j = 1 } ^ { n } b _ { j } \right|. \end{equation*}
Also, if $P _ { j } ( x )$ are polynomials of degree $k_j - 1$, $G _ { 1 } ( r ) = \sum _ { j = 1 } ^ { n } P _ { j } ( r ) z _ { j } ^ { r }$ and $K = k _ { 1 } + \ldots + k _ { n }$, then $\operatorname {max}_{r}\operatorname { Re } G _ { 1 } ( r ) \geq B$ and $\min_r \operatorname{Re} G _ { 1 } ( r ) \leq - B$, where
\begin{equation*} B = \frac { 1 } { 6 K } \left( \frac { K } { 4 e ( m + 2 K ) } \right) ^ { 2 K } \left| \operatorname { Re } \sum _ { j = 0 } ^ { n } P _ { j } ( 0 ) \right| \end{equation*}
and the range of $r$ is $[ m + 1 , m + K ( 3 + \pi / \kappa ) ]$.
Assume now that $\operatorname {max}_{j} | z _ { j } | = 1$. Let $G _ { 2 } ( r )$ be as defined above, and assume $\phi ( z ) \neq 0$ for $z \in \{ | z | \geq \rho \} \cup \{ | \operatorname { arc } z | < \kappa \}$, where $0 < \rho < 1$ and $0 < \kappa < \pi / 2$. Assume also that $\kappa \leq | \operatorname { arc } z _ { j } | < \pi$, $j = 1 , \ldots , n$. Take any $\delta _ { 1 }$, $\delta _ { 2 }$ satisfying $1 > \delta _ { 1 } > \delta _ { 2 } \geq \rho$ and define $h_{1}$, $h _ { 2 }$ by
\begin{equation*} 1 = | z _ { 1 } | \geq \ldots \geq | z _ { h _ { 1 } } | \geq \delta _ { 1 } > \end{equation*}
\begin{equation*} > | z _ { h _ { 1 } } + 1 | \geq \ldots \geq | z _ { h _ { 2 } } | > \delta _ { 2 } \geq \end{equation*}
\begin{equation*} \geq | z _ { h_2 } + 1 | \geq \ldots \geq | z _ { n } |. \end{equation*}
(If $h_{1}$ or $h _ { 2 }$ do not exist, replace them with $n$.) Put $I = [ m + 1 , m + ( n + k ) ( 3 + \pi / k ) ]$ and
\begin{equation*} M = \frac { 1 } { 3 ( n + k ) } \left( \frac { \delta _ { 1 } - \delta _ { 2 } } { 16 } \right) ^ { 2 n + 2 k } \delta _ { 2 } ^ { m + ( n + k ) ( 1 + \pi / k ) }\times \end{equation*}
\begin{equation*} \times \operatorname { min } _ { h _ { 1 } \leq j \leq h _ { 2 } } | \operatorname { Re } ( b _ { 1 } + \ldots + b _ { j } ) |. \end{equation*}
Then $\max_{r \in I} \text{Re} \, G_2 (r ) \geq M$ and $\operatorname{min}_{r\in I} \operatorname{Re} G _ { 2 } ( r ) \leq - M$. If $\phi ( z ) = 1$, then the above result holds with $k = \rho = 0$.
J.D. Buchholtz [a5], [a6] proved that if $\operatorname {max}_{j} | z _ { j } | = 1$, then
\begin{equation*} \operatorname { max } _ { k = 1 , \ldots , n } \left( \frac { 1 } { n } | s _ { k } | \right) ^ { 1 / k } > \frac { 1 } { 5 } > \frac { 1 } { 2 + \sqrt { 8 } }, \end{equation*}
respectively, where the last result is the best possible.
R. Tijdeman [a47] proved the following result for "operator-type problems" .
Let $P _ { j } ( x )$ be fixed complex polynomials of degree $k_j - 1$ and let $G _ { 1 } ( k ) = \sum _ { j = 1 } ^ { n } P _ { j } ( k ) z _ { j } ^ { k }$. Then for every integer $m \geq 0$, $K = k _ { 1 } + \ldots + k _ { n }$, and $\operatorname{min}_{j} | z _ { j } | = 1$, the inequality
\begin{equation} \tag{a3} \operatorname { min } _ { r = m + 1 , \ldots , m + K } | G _ { 1 } ( r ) | \geq \frac { 1 } { P _ { m , K } } \left| \sum _ { j = 1 } ^ { n } P _ { j } ( 0 ) \right| \end{equation}
holds, where $P _ { m , K }$ is defined above and the factor $1 / P _ { m , K}$ is the best possible; also, if $\operatorname {max}_{j} | z _ { j } | = 1$, then (a3) holds with $( K / ( 8 e ( m + K ) ) ) ^ { K }$ instead of $1 / P _ { m , K}$.
J. Geysel [a17] improved the above constant to
\begin{equation*} \frac { 1 } { 4 } \left( \frac { K - 1 } { 8 e ( m + K ) } \right) ^ { K }. \end{equation*}
Turán studied the other "operator-type problem" for $G _ { 2 } ( r ) = \sum _ { j = 1 } ^ { n } b _ { j } \phi ( z _ { j } ) z _ { j } ^ { k }$. Let $b _ { j }$ be fixed complex numbers and let $\phi ( z ) = z ^ { k } + a _ { 1 } z ^ { k - 1 } + \ldots + a _ { k }$ be a polynomial with no zeros outside $| z | < \rho$. Assume that $m > - 1$, $0 < \rho < 1$ and $\operatorname {max}_{j} | z _ { j } | = 1$. Then
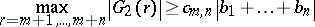 | (a4) |
with
\begin{equation*} c _ { m , n } = 2 ^ { - n } \left( \frac { 1 + \rho } { 2 } \right) ^ { m } \left( \frac { 1 - \rho } { 2 } \right) ^ { n + k }. \end{equation*}
In case of the maximum norm and $1 = | z _ { 1 } | \geq \ldots \geq | z _ { n } | > 0$, Turán proved (a4) with
\begin{equation*} c _ { m ,\, n } = \left\{ \begin{array} { l l } { 2 ^ { 1 - n } \left( \frac { n + k } { 4 e ( m + n + k ) } \right) ^ { n + k } } & { \text { if } \frac { m } { m + n + k } \geq \rho, } \\ { \rho ^ { m } 2 ^ { 1 - n } \left( \frac { 1 - \rho } { 4 } \right) ^ { n + k } } & { \text { if } \frac { m } { m + n + k } < \rho. } \end{array} \right. \end{equation*}
He also proved the following "simultaneous problem" . Let $\operatorname{min}_j | z _ { j } | = \operatorname { min } _ { j } | w _ { j } | = 1$. For any integers $m > - 1$ and $n _ { 1 } , n _ { 2 } \geq 1$ there exist a $ k \in [ m + 1 , m + n _ { 1 } n _ { 2 } ]$ such that the inequalities
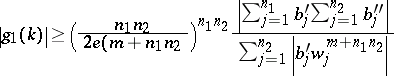 |
and
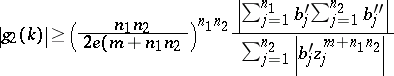 |
hold simultaneously.
References
| [a1] | J. Anderson, "On some power sum problems of Turan and Erdos" Acta Math. Hung. , 70 : 4 (1996) pp. 305–316 |
| [a2] | F.V. Atkinson, "Some further estimates concerning sums of powers of complex numbers" Acta Math. Hung. , XX : 1–2 (1969) pp. 193–210 |
| [a3] | A. Biro, "On a problem of Turan concerning sums of powers of complex numbers" Acta Math. Hung. , 65 : 3 (1994) pp. 209–216 |
| [a4] | N.G. de Bruijn, "On Turan's first main theorem" Acta Math. Hung. , XI : 3–4 (1960) pp. 213–216 |
| [a5] | J.D. Buchholtz, "Extremal problems for sums of powers of complex numbers" Acta Math. Hung. , XVII (1966) pp. 147–153 |
| [a6] | J.D. Buchholtz, "Sums of complex numbers" J. Math. Anal. Appl. , 17 (1967) pp. 269–279 |
| [a7] | J.W.S. Cassels, "On the sums of powers of complex numbers" Acta Math. Hung. , VII : 3–4 (1956) pp. 283–290 |
| [a8] | S. Dancs, "On generalized sums of powers of complex numbers" Ann. Univ. Sci. Budapest. Eotvos Sect. Math. , VII (1964) pp. 113–121 |
| [a9] | S. Dancs, P. Turan, "On the distribution of values of a class of entire functions I" Publ. Math. Debrecen , 11 : 1–4 (1964) pp. 257–265 |
| [a10] | S. Dancs, P. Turan, "On the distribution of values of a class of entire functions II" Publ. Math. Debrecen , 11 (1964) pp. 266–272 |
| [a11] | S. Dancs, P. Turan, "Investigations in the power sum theory I" Ann. Univ. Sci. Budapest. Eotvos Sect. Math. , XVI (1973) pp. 47–52 |
| [a12] | S. Dancs, P. Turan, "Investigations in the power sum theory II" Acta Arith. , XXV (1973) pp. 105–113 |
| [a13] | S. Dancs, P. Turan, "Investigations in the power sum theory III" Ann. Mat. Pura Appl. , CIII (1975) pp. 199–205 |
| [a14] | S. Dancs, P. Turan, "Investigations in the power sum theory IV" Publ. Math. Debrecen , 22 (1975) pp. 123–131 |
| [a15] | L. Erdös, "On some problems of P. Turan concerning power sums of complex numbers" Acta Math. Hung. , 59 : 1–2 (1992) pp. 11–24 |
| [a16] | P. Erdos, P. Turan, "On a problem in the theory of uniform distribution I and II" Indag. Math. , X : 5 (1948) pp. 3–11; 12–19 |
| [a17] | J.M. Geysel, "On generalized sums of powers of complex numbers" M.C. Report Z.W. (Math. Centre, Amsterdam) , 1968–013 (1968) |
| [a18] | S.M. Gonek, "A note on Turan's method" Michigan Math. J. , 28 : 1 (1981) pp. 83–87 |
| [a19] | G. Halasz, "On the first and second main theorem in Turan's theory of power sums" , Studies Pure Math. , Birkhäuser (1983) pp. 259–269 |
| [a20] | G. Halasz, P. Turan, "On the distribution of roots or Riemann zeta and allied problems I" J. Number Th. , I (1969) pp. 122–137 |
| [a21] | G. Halasz, P. Turan, "On the distribution of roots or Riemann zeta and allied problems II" Acta Math. Hung. , XXI : 3–4 (1970) pp. 403–419 |
| [a22] | S. Knapowski, P. Turan, "The comparative theory of primes I" Acta Math. Hung. , XIII : 3–4 (1962) pp. 299–314 |
| [a23] | S. Knapowski, P. Turan, "The comparative theory of primes II" Acta Math. Hung. , XIII (1962) pp. 315–342 |
| [a24] | S. Knapowski, P. Turan, "The comparative theory of primes III" Acta Math. Hung. , XIII (1962) pp. 343–364 |
| [a25] | S. Knapowski, P. Turan, "The comparative theory of primes IV" Acta Math. Hung. , XIV : 1–2 (1963) pp. 31–42 |
| [a26] | S. Knapowski, P. Turan, "The comparative theory of primes V" Acta Math. Hung. , XIV (1963) pp. 43–64 |
| [a27] | S. Knapowski, P. Turan, "The comparative theory of primes VI" Acta Math. Hung. , XIV (1963) pp. 65–78 |
| [a28] | S. Knapowski, P. Turan, "The comparative theory of primes VII" Acta Math. Hung. , XIV : 3–4 (1963) pp. 241–250 |
| [a29] | S. Knapowski, P. Turan, "The comparative theory of primes VIII" Acta Math. Hung. , XIV (1963) pp. 251–268 |
| [a30] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory I" Acta Arith. , IX : 1 (1964) pp. 23–40 |
| [a31] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory II" Acta Arith. , IX : 3 (1964) pp. 293–314 |
| [a32] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory III" Acta Arith. , XI : 1 (1965) pp. 115–127 |
| [a33] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory IV" Acta Arith. , XI : 2 (1965) pp. 147–162 |
| [a34] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory V" Acta Arith. , XI (1965) pp. 193–202 |
| [a35] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory VI" Acta Arith. , XII : 1 (1966) pp. 85–96 |
| [a36] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory VII" Acta Arith. , XXI (1972) pp. 193–201 |
| [a37] | S. Knapowski, P. Turan, "On the sign changes of $* ( x ) - \text { li } x$" Topics in Number Theory (Colloq. Math. Soc. J. Bolyai) , 13 (1976) pp. 153–170 |
| [a38] | S. Knapowski, P. Turan, "On the sign changes of $* ( x ) - \text { li } x$ II" Monatsh. Math. , 82 (1976) pp. 163–175 |
| [a39] | S. Knapowski, P. Turan, "On an assertion of Cebysev" J. d'Anal. Math. , XIV (1965) pp. 267–274 |
| [a40] | S. Knapowski, P. Turan, "Uber einige Fragen der vergleichenden Primzahltheorie" , Abhandl. aus der Zahlentheorie und Analysis , VEB Deutsch. Verlag Wiss. (1968) pp. 159–171 |
| [a41] | S. Knapowski, P. Turan, "On prime numbers $* 1$ resp. $3 ( 4 )$" H. Zassenhaus (ed.) , Number Theory and Algebra , Acad. Press (1977) pp. 157–166 |
| [a42] | G. Kolesnik, E.G. Straus, "On the sum of powers of complex numbers" , Studies Pure Math. , Birkhäuser (1983) pp. 427–442 |
| [a43] | J. Komlos, A. Sarcozy, E. Szemeredi, "On sums of powers of complex numbers" Mat. Lapok , XV : 4 (1964) pp. 337–347 (In Hungarian) |
| [a44] | E. Makai, "An estimation in the theory of diophantine approximations" Acta Math. Hung. , IX : 3–4 (1958) pp. 299–307 |
| [a45] | E. Makai, "On a minimum problem" Acta Math. Hung. , XV : 1–2 (1964) pp. 63–66 |
| [a46] | V.T. Sos, P. Turan, "On some new theorems in the theory of diophantine approximations" Acta Math. Hung. , VI : 3–4 (1955) pp. 241–257 |
| [a47] | R. Tijdeman, "On the distribution of the values of certain functions" PhD Thesis Univ. Amsterdam (1969) |
| [a48] | P. Turan, "Ueber die Verteilung der Primzahlen I" Acta Sci. Math. (Szeged) , X (1941) pp. 81–104 |
| [a49] | P. Turan, "On a theorem of Littlewood" J. London Math. Soc. , 21 (1946) pp. 268–275 |
| [a50] | P. Turan, "Sur la theorie des fonctions quasianalytiques" C.R. Acad. Sci. Paris (1947) pp. 1750–1752 |
| [a51] | P. Turan, "On the gap theorem of Fabry" Acta Math. Hung. , I (1947) pp. 21–29 |
| [a52] | P. Turan, "On Riemann's hypotesis" Acad. Sci. URSS Bull. Ser. Math. , 11 (1947) pp. 197–262 |
| [a53] | P. Turan, "On a new method in the analysis with applications" Casopis Pro Pest. Mat. A Fys. Rc. , 74 (1949) pp. 123–131 |
| [a54] | P. Turan, "On the remainder term of the prime-number formula I" Acta Math. Hung. , I : 1 (1950) pp. 48–63 |
| [a55] | P. Turan, "On the remainder term of the prime-number formula II" Acta Math. Hung. , I : 3–4 (1950) pp. 155–166 |
| [a56] | P. Turan, "On approximate solution of algebraic equations" Publ. Math. Debrecen. , II : 1 (1951) pp. 28–42 |
| [a57] | P. Turan, "On Carlson's theorem in the theory of zetafunction of Riemann" Acta Math. Hung. , II : 1–2 (1951) pp. 39–73 |
| [a58] | P. Turan, "On a property of lacunary power-series" Acta Sci. Math. (Szeged) , XIV : 4 (1952) pp. 209–218 |
| [a59] | P. Turan, "Uber eine neue Methode der Analysis und ihre Anwendungen" , Akad. Kiado (1953) |
| [a60] | P. Turan, "On Lindelof's conjecture" Acta Math. Hung. , V : 3–4 (1954) pp. 145–153 |
| [a61] | P. Turan, "Uber eine neue Methode der Analysis und ihre Anwendungen" , Akad. Kiado (1956) (Rev. Chinese ed.) |
| [a62] | P. Turan, "On the instability of systems of differential equations" Acta Math. Hung. , VI : 3–4 (1955) pp. 257–271 |
| [a63] | P. Turan, "On the zeros of the zetafunction of Riemann" J. Indian Math. Soc. , XX (1956) pp. 17–36 |
| [a64] | P. Turan, "Uber eine neue Methode der Analysis" Wissenschaftl. Z. Humboldt Univ. Berlin (1955/56) pp. 275–279 |
| [a65] | P. Turan, "Uber eine Anwendung einer neuen Methode auf die Theorie der Riemannschen Zetafunktion" Wissenschaftl. Z. Humboldt Univ. Berlin (1955/56) pp. 281–285 |
| [a66] | P. Turan, "Remark on the preceding paper of J.W.S. Cassels" Acta Math. Hung. , VII : 3–4 (1957) pp. 291–294 |
| [a67] | P. Turan, "Remark on the theory of quasianalytic function classes" Publ. Math. Inst. Hung. Acad. Sci. , I : 4 (1956) pp. 481–487 |
| [a68] | P. Turan, "Uber lakunaren Potenzreihen" Rev. Math. Pures Appl. , I (1956) pp. 27–32 |
| [a69] | P. Turan, "On the so-called density hypothesis of zeta-function of Riemann" Acta Arith. , IV : 1 (1958) pp. 31–56 |
| [a70] | P. Turan, "Zur Theorie der Dirichletschen Reihen" Euler Festschr. (1959) pp. 322–336 |
| [a71] | P. Turan, "On a property of the stable or conditionally stable solutions of systems of nonlinear differential equations" Ann. of Math. , XLVIII (1959) pp. 333–340 |
| [a72] | P. Turan, "A note on the real zeros of Dirichlet L-functions" Acta Arith. , V (1959) pp. 309–314 |
| [a73] | P. Turan, "On the distribution of zeros of general exponential polynomials" Publ. Math. Debrecen. , VII (1960) pp. 130–136 |
| [a74] | P. Turan, "On an improvement of some new one-sided theorems of the theory of diophantine approximations" Acta Math. Hung. , XI : 3–4 (1960) pp. 299–316 |
| [a75] | P. Turan, "On a density theorem of Ju.V. Linnik" Publ. Math. Inst. Hung. Acad. Sci. Ser.A , VI : 1–2 (1961) pp. 165–179 |
| [a76] | P. Turan, "On the eigenvalues of matrices" Ann. Mat. Pura Appl. , IV (LIV) (1961) pp. 397–401 |
| [a77] | P. Turan, "On some further one-sided theorems of new type" Acta Math. Hung. , XII : 3–4 (1961) pp. 455–468 |
| [a78] | P. Turan, "A remark on the heat equation" J. d'Anal. Math. , XIV (1965) pp. 443–448 |
| [a79] | P. Turan, "On a certain limitation of eigenvalues of matrices" Aequat. Math. , 2 : 2–3 (1969) pp. 184–189 |
| [a80] | P. Turan, "On the approximate solutions of algebraic equations" Commun. Math. Phys. Class Hung. Acad. , XVIII (1968) pp. 223–236 (In Hungarian) |
| [a81] | P. Turan, "A remark on linear differential equations" Acta Math. Hung. , XX : 3–4 (1969) pp. 357–360 |
| [a82] | P. Turan, "Zeta roots and prime numbers" Colloq. Math. Soc. Janos Bolyai (Number Theory) , 2 (1969) pp. 205–216 |
| [a83] | P. Turan, "Exponential sums and the Riemann conjecture" , Analytic Number Theory , Proc. Symp. Pure Math. , XXIV , Amer. Math. Soc. (1973) pp. 305–314 |
| [a84] | P. Turan, "On an inequality of Cebysev" Ann. Univ. Sci. Budapest. Eotvos Sect. Math. , XI (1968) pp. 15–16 |
| [a85] | P. Turan, "On an inequality" Ann. Univ. Sci. Budapest. Eotvos Sect. Math. , I (1958) pp. 3–6 |
| [a86] | P. Turan, "On a certain problem in the theory of power series with gaps" , Studies Math. Anal. Rel. Topics , Stanford Univ. Press (1962) pp. 404–409 |
| [a87] | P. Turan, "On a trigonometric inequality" , Proc. Constructive Theory of Functions , Akad. Kiado (1969) pp. 503–512 |
| [a88] | P. Turan, "Investigations in the power sum theory II (with S. Dancs)" Acta Arith. , XXV (1973) pp. 105–113 |
| [a89] | P. Turan, "On the latent roots of $*$-matrices" Comput. Math. Appl. (1975) pp. 307–313 |
| [a90] | P. Turan, "On some recent results in the analytical theory of numbers" , Proc. Symp. Pure Math. , XX , Inst. Number Theory (1969) pp. 359–374 |
| [a91] | P. Turan, "On a new method of analysis and its applications" , Wiley (1984) |
Turán theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tur%C3%A1n_theory&oldid=50037