Difference between revisions of "3-Sasakian manifold"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (AUTOMATIC EDIT (latexlist): Replaced 150 formulas out of 153 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 153 formulas, 150 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | Sasakian and $3$-Sasakian spaces are odd-dimensional companions of Kähler and hyper-Kähler manifolds, respectively. A [[Riemannian manifold|Riemannian manifold]] $( \mathcal{S} , g )$ of dimension $m$ is called Sasakian if the [[Holonomy group|holonomy group]] of the metric cone $( C ( \mathcal{S} ) , \overline { g } ) = ( \mathbf{R} _ { + } \times \mathcal{S} , d r ^ { 2 } + r ^ { 2 } g )$ reduces to a subgroup of $U ( ( m + 1 ) / 2 )$. In particular, $m = 2l + 1$, $l \geq 1$, and such a cone is a [[Kähler manifold|Kähler manifold]]. Let $I$ be a [[Complex structure|complex structure]] on $C ( \mathcal S )$. Then $\xi = I ( \partial _ { r } )$ restricted to $\mathcal{S}$ is a unit Killing vector field (cf. also [[Killing vector|Killing vector]]) with the property that the [[Sectional curvature|sectional curvature]] of every section containing $\xi $ equals one. Such a $\xi $ is called the characteristic vector field on $\mathcal{S}$ and its properties can be used as an alternative characterization of a Sasakian manifold. | ||
| − | + | Similarly, one says that $( \mathcal{S} , g )$ is a $3$-Sasakian manifold if the holonomy group of the metric cone $( C ( \mathcal{S} ) , \overline { g } )$ reduces to a subgroup of $\operatorname { Sp } ( ( m + 1 ) / 4 )$. In particular, $m = 4 n + 3$, $n \geq 1$, and the cone is a hyper-Kähler manifold. When $\mathcal{S}$ is $3$-Sasakian, the hyper-Kähler structure on the associated cone $C ( \mathcal S )$ can be used to define three vector fields $\xi ^ {a } = I ^ { a} ( \partial _ { r } )$, $a = 1,2,3$, where $\{ I ^ { 1 } , I ^ { 2 } , I ^ { 3 } \}$ is a hypercomplex structure on $C ( \mathcal S )$. It follows that, when restricted to $\mathcal{S}$, $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ are Killing vector fields such that $g ( \xi ^ { a } , \xi ^ { b } ) = \delta _ { a b }$ and $[ \xi ^ {a } , \xi ^ { b } ] = 2 \epsilon _ { a b c } \xi ^ { c }$. Hence, they are orthonormal and locally define an isometric $ \operatorname {SO} ( 3 )$ (or $\operatorname{SU} ( 2 )$) action on $\mathcal{S}$. In turn, the triple $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ yields $\eta ^ { a } ( Y ) = g ( \xi ^ { a } , Y )$ and $\Phi ^ { a } ( Y ) = \nabla _ { Y } \xi ^ { a }$ for each $a = 1,2,3$. The collection of tensors $\{ \xi ^ { a } , \eta ^ { a } , \Phi ^ { a } \}_{a = 1,2,3}$ is traditionally called the $3$-Sasakian structure on $( \mathcal{S} , g )$. This is the way such structures were first introduced in the work of C. Udrişte [[#References|[a1]]] and Y. Kuo [[#References|[a2]]] in 1969 and 1970. | |
| − | + | Every $3$-Sasakian manifold is an Einstein manifold with positive Einstein constant $\lambda = \operatorname { dim } ( \mathcal{S} ) - 1$. If $\mathcal{S}$ is complete, it is compact with finite [[Fundamental group|fundamental group]]. If $( \mathcal{S} , g )$ is compact, the characteristic vector fields $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ are complete and define a $3$-dimensional [[Foliation|foliation]] $\mathcal{F} _ { 3 }$ on $\mathcal{S}$. The leaves of this foliation are necessarily compact, since $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ defines a locally free $\operatorname{SU} ( 2 )$ action on $\mathcal{S}$. Hence, the foliation $\mathcal{F} _ { 3 }$ is automatically almost-regular and the space of leaves is a compact orbifold, denoted by $\mathcal{O}$. The leaves of $\mathcal{F} _ { 3 }$ are totally geodesic submanifolds of constant sectional curvature equal one (cf. also [[Totally-geodesic manifold|Totally-geodesic manifold]]). They are all $3$-dimensional homogeneous spherical space forms $S ^ { 3 } / \Gamma$, where $\Gamma \subset \operatorname{SU} ( 2 )$ is a finite subgroup (cf. also [[Space forms|Space forms]]). In particular, the leaves are $3$-Sasakian manifolds themselves. The space of leaves $\mathcal{O}$ is a compact positive quaternion Kähler orbifold. The principal leaves are always diffeomorphic to either $S ^ { 3 }$ or $ \operatorname {SO} ( 3 )$. A compact $3$-Sasakian manifold is said to be regular if $\mathcal{F} _ { 3 }$ is regular, i.e., if all the leaves are diffeomorphic. In this case $\mathcal{O}$ is a smooth manifold (cf. [[Differentiable manifold|Differentiable manifold]]). For any $\tau = ( \tau _ { 1 } , \tau _ { 2 } , \tau _ { 3 } ) \in \mathbf{R} ^ { 3 }$ such that $\tau _ { 1 } ^ { 2 } + \tau _ { 3 } ^ { 2 } + \tau _ { 3 } ^ { 2 } = 1$, the vector field $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$ has the Sasakian property. Hence, a $3$-Sasakian manifold has a $2$-sphere worth of Sasakian structures (just as hyper-Kähler manifold has an $S ^ { 2 }$-worth of complex structures). When $\mathcal{S}$ is compact, the vector field $\xi ( \tau )$ defines a $1$-dimensional foliation $\mathcal{F} _ { \tau } \subset \mathcal{F} _ { 3 } \subset \mathcal{S}$ with compact leaves. Such a foliation gives $\mathcal{S}$ an isometric locally free circle action $U ( 1 ) _ { \tau } \subset \operatorname { SU } ( 2 )$. The space of leaves $\mathcal{Z} = \mathcal{S} / \mathcal{F} _ { \tau }$ is a compact Kähler–Einstein orbifold of positive scalar curvature. It is a simply-connected normal projective algebraic variety (cf. [[Projective algebraic set|Projective algebraic set]]). $\mathcal Z$ has a complex [[Contact structure|contact structure]] and it is a $\mathbf{Q}$-factorial Fano variety (cf. also [[Fano variety|Fano variety]]). It is an orbifold twistor space of $\mathcal{O}$. All the foliations associated to $\mathcal{S}$ can be described in the the following diagram <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001088.png"/> of orbifold fibrations: | |
| − | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001089.png"/></td> </tr></table> | |
| − | + | All four geometries in the above diagram are Einstein. Both $\mathcal{S}$ and $\mathcal Z$ admit second, non-isometric Einstein metrics of positive scalar curvature. Every $3$-Sasakian manifold is a spin manifold (cf. [[Spinor structure|Spinor structure]]). When $\mathcal{S}$ is complete, simply-connected and not of constant curvature, it admits $n + 2$ Killing spinors, where $\operatorname { dim } ( {\cal S} ) = 4 n + 3$. The holonomy group of $\mathcal{S}$ never reduces to a proper subgroup of $\operatorname{SO} ( 4 n + 3 )$ and the metric admits no infinitesimal deformations. | |
| − | + | For every compact semi-simple [[Lie group|Lie group]] $G$ one has a corresponding diagram $^{ \bigtriangleup } _ { \bigtriangledown } ( G / K )$ with ${\cal O} = G / \operatorname { Sp } ( 1 ) . K$ being a symmetric positive quaternion Kähler manifold (a Wolf space) and $\mathcal{Z} = G / U ( 1 ) . K$. In particular, every every $3$-Sasakian $G$-homogeneous space is regular and it is one of the spaces | |
| − | + | \begin{equation*} \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times \mathbf{Z} _ { 2 }, \end{equation*} | |
| − | + | \begin{equation*} \operatorname {SU} ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , \operatorname {SO} ( k ) / \operatorname {SO} ( k - 4 ) \times \operatorname {Sp} ( 1 ), \end{equation*} | |
| − | + | \begin{equation*} G _ { 2 } / \operatorname { Sp } ( 1 ) , \quad F _ { 4 } / \operatorname { Sp } ( 3 ) , E _ { 6 } / \operatorname{SU} ( 6 ) , \quad E _ { 7 } / \operatorname { Spin } ( 12 ) , \quad E _ { 8 } / E _ { 7 }. \end{equation*} | |
| − | + | Here, $n \geq 0$, $\operatorname{Sp} ( 0 )$ denotes the trivial group, $m > 3$, and $k \geq 7$. Hence, there is one-to-one correspondence between the simple Lie algebras and the simply-connected $3$-Sasakian homogeneous manifolds. | |
| − | + | There is a conjecture that all complete regular $3$-Sasakian manifolds are homogeneous. It is a simple translation of the corresponding conjecture due to C. LeBrun and S. Salamon [[#References|[a3]]] that all positive quaternion Kähler manifolds are symmetric. This is known to be true when $\operatorname { dim } ( {\cal S} ) = 7$ or $11$ ($\operatorname { dim } ( \mathcal{O} ) = 4$ or $8$). More generally, it is know that in each dimension $4 n + 3$, there are only finitely many complete regular $3$-Sasakian manifolds, all of them having $b _ { 2 } ( \mathcal{S} ) \leq 1$ with equality holding only when $\mathcal{S} = \text{SU} ( m ) / S ( U ( m - 2 ) \times U ( 1 ) )$. Furthermore, it was shown by K. Galicki and S. Salamon [[#References|[a4]]] that each [[Betti number|Betti number]] of such an $\mathcal{S}$ must satisfy the linear relation | |
| − | + | \begin{equation*} \sum _ { k = 1 } ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0 \end{equation*} | |
| − | + | with odd Betti numbers $b _ { 2i + 1} ( \mathcal{S} ) = 0$ for $ { i } \leq n$. In fact the vanishing of odd Betti numbers holds true in the irregular case as well. There are, however, examples of an $11$-dimensional irregular $3$-Sasakian manifold for which $b _ { 2 } \neq b _ { 4 }$ and of $15$-dimensional manifolds with $b _ { 2 } \neq b _ { 6 }$. These were constructed explicitly by C. Boyer, K. Galicki and B. Mann [[#References|[a5]]]. | |
| + | |||
| + | The first complete irregular examples that are not quotients of homogeneous spaces by a discrete group of isometries were obtained also by Boyer, Galicki and Mann [[#References|[a10]]], [[#References|[a11]]], [[#References|[a12]]], [[#References|[a13]]], [[#References|[a14]]], [[#References|[a15]]], using a method called $3$-Sasakian reduction. The examples are bi-quotients of unitary groups of the form $\mathcal{S} ( p ) = U ( 1 ) _ { p } \backslash U ( n + 2 ) / U ( n )$. The $( 4 n + 3 )$-dimensional family ${\cal S} ( \operatorname{p} )$ depends on positive integral "weights" $\operatorname{p} = ( p _ { 1 } , \dots , p _ { n + 2} )$ which are pairwise relatively prime. The integral cohomology ring of ${\cal S} ( \operatorname{p} )$ depends on the weight vector $\text{p}$ and one gets infinitely many homotopy types of compact simply-connected $3$-Sasakian manifolds in each allowable dimension $\geq 7$. Other irregular examples were constructed later in dimension $7$, $11$, $15$ by Boyer, Galicki, Mann, and E. Rees [[#References|[a6]]]. The same method of $3$-Sasakian reduction was used to obtain families of compact simply-connected $3$-Sasakian $7$-manifolds with an arbitrary second Betti number. All these examples are toric, i.e., having $T ^ { 2 } \times \operatorname { Sp } ( 1 )$ or $T ^ { 2 } \times SO ( 3 )$ as the group of isometries with the $2$-torus action preserving the $3$-Sasakian structure. R. Bielawski [[#References|[a7]]] showed that, in any dimension $4 n + 3$, a toric $3$-Sasakian manifold is necessarily diffeomorphic to one of the quotients obtained in [[#References|[a6]]]. Examples of compact $3$-Sasakian manifold which are not toric can also be constructed. | ||
| + | |||
| + | After their introduction in 1969, $3$-Sasakian manifolds were vigorously studied by a group of Japanese geometers, including S. Ishihara, T. Kashiwada, M. Konishi, Y. Kuo, S. Tachibana, S. Tanno, and W.N. Yu [[#References|[a16]]], [[#References|[a17]]], [[#References|[a18]]], [[#References|[a19]]], [[#References|[a20]]], [[#References|[a21]]], [[#References|[a22]]], [[#References|[a23]]]. This lasted until 1975, when the whole subject was relegated to an almost complete obscurity largely due to lack of any interesting examples. In the early 1990s $3$-Sasakian manifolds returned in two different areas. One of them is the study of $7$-manifolds admitting Killing spinors, in the work of T. Friedrich and I. Kath [[#References|[a8]]]. The other is the work [[#References|[a10]]], [[#References|[a11]]], [[#References|[a12]]], [[#References|[a13]]], [[#References|[a14]]], [[#References|[a15]]], of Boyer–Galicki–Mann, in which the first irregular examples are constructed and a systematic study of geometry and topology of compact $3$-Sasakian manifolds is undertaken. | ||
For a detailed review of the subject and extensive bibliography see [[#References|[a9]]]. | For a detailed review of the subject and extensive bibliography see [[#References|[a9]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> C. Udrişte, "Structures presque coquaternioniennes" ''Bull. Math. Soc. Sci. Math. Roum.'' , '''12''' (1969) pp. 487–507 {{MR|0296849}} {{ZBL|0213.48205}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> Y.-Y. Kuo, "On almost contact 3-structure" ''Tôhoku Math. J.'' , '''22''' (1970) pp. 325–332 {{MR|0278225}} {{ZBL|0205.25801}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> K. Galicki, S. Salamon, "On Betti numbers of 3-Sasakian manifolds" ''Geom. Dedicata'' , '''63''' (1996) pp. 45–68 {{MR|1413621}} {{ZBL|}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> C. LeBrun, S.M. Salamon, "Strong rigidity of positive quaternion–Kähler manifolds" ''Invent. Math.'' , '''118''' (1994) pp. 109–132</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "A note on smooth toral reductions of spheres" ''Manuscripta Math.'' , '''95''' (1998) pp. 149–158 {{MR|1603301}} {{ZBL|0913.53020}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, E. Rees, "Compact 3-Sasakian 7-manifolds with arbitrary second Betti number" ''Invent. Math.'' , '''131''' (1998) pp. 321–344 {{MR|1608567}} {{ZBL|0901.53033}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> R. Bielawski, "Complete $T ^ { n }$-invariant hyperkähler $4 n$-manifolds" ''MPI preprint'' , '''65''' (1998) (www.mpim-bonn.mpg.de/html/preprints/preprints.html)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> T. Friedrich, I. Kath, "Compact seven-dimensional manifolds with Killing spinors" ''Comm. Math. Phys.'' , '''133''' (1990) pp. 543–561</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> C.P. Boyer, K. Galicki, "3-Sasakian Manifolds" C. LeBrun (ed.) M. Wang (ed.) , ''Essays on Einstein Manifolds'' , Internat. Press (to appear) {{MR|1798609}} {{MR|1645769}} {{MR|1433200}} {{MR|1293878}} {{MR|1249451}} {{ZBL|1008.53047}} {{ZBL|0942.53030}} {{ZBL|0901.53033}} {{ZBL|0889.53029}} {{ZBL|0814.53037}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "Quaternionic reduction and Einstein manifolds" ''Commun. Anal. Geom.'' , '''1''' (1993) pp. 1–51 {{MR|1243524}} {{ZBL|0856.53038}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "The geometry and topology of 3-Sasakian manifolds" ''J. Reine Angew. Math.'' , '''455''' (1994) pp. 183–220 {{MR|1293878}} {{ZBL|0889.53029}} </td></tr><tr><td valign="top">[a12]</td> <td valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "New examples of inhomogeneous Einstein manifolds of positive scalar curvature" ''Math. Res. Lett.'' , '''1''' (1994) pp. 115–121 {{MR|1258497}} {{ZBL|0842.53033}} </td></tr><tr><td valign="top">[a13]</td> <td valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "3-Sasakian manifolds" ''Proc. Japan Acad. Ser. A'' , '''69''' (1993) pp. 335–340 {{MR|1249451}} {{ZBL|0814.53037}} </td></tr><tr><td valign="top">[a14]</td> <td valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "Hypercomplex structures on Stiefel manifolds" ''Ann. Global Anal. Geom.'' , '''14''' (1996) pp. 81–105 {{MR|1375068}} {{ZBL|0843.53030}} </td></tr><tr><td valign="top">[a15]</td> <td valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "New examples of inhomogeneous Einstein manifolds of positive scalar curvature" ''Bull. London Math. Soc.'' , '''28''' (1996) pp. 401–408 {{MR|1258497}} {{ZBL|0842.53033}} </td></tr><tr><td valign="top">[a16]</td> <td valign="top"> S. Ishihara, M. Konishi, "Fibered Riemannian spaces with Sasakian 3-structure" , ''Differential Geometry, in Honor of K. Yano'' , Kinokuniya (1972) pp. 179–194</td></tr><tr><td valign="top">[a17]</td> <td valign="top"> S. Ishihara, "Quaternion Kählerian manifolds and fibered Riemannian spaces with Sasakian 3-structure" ''Kodai Math. Sem. Rep.'' , '''25''' (1973) pp. 321–329</td></tr><tr><td valign="top">[a18]</td> <td valign="top"> T. Kashiwada, "A note on a Riemannian space with Sasakian 3-structure" ''Nat. Sci. Rep. Ochanomizu Univ.'' , '''22''' (1971) pp. 1–2 {{MR|0303449}} {{ZBL|0228.53033}} </td></tr><tr><td valign="top">[a19]</td> <td valign="top"> M. Konishi, "On manifolds with Sasakian 3-structure over quaternion Kählerian manifolds" ''Kodai Math. Sem. Rep.'' , '''26''' (1975) pp. 194–200</td></tr><tr><td valign="top">[a20]</td> <td valign="top"> Y.-Y. Kuo, S. Tachibana, "On the distribution appeared in contact 3-structure" ''Taita J. Math.'' , '''2''' (1970) pp. 17–24 {{MR|0309004}} {{ZBL|0231.53053}} </td></tr><tr><td valign="top">[a21]</td> <td valign="top"> S. Tachibana, W.N. Yu, "On a Riemannian space admitting more than one Sasakian structure" ''Tôhoku Math. J.'' , '''22''' (1970) pp. 536–540 {{MR|0275329}} {{ZBL|}} </td></tr><tr><td valign="top">[a22]</td> <td valign="top"> S. Tanno, "Killing vectors on contact Riemannian manifolds and fiberings related to the Hopf fibrations" ''Tôhoku Math. J.'' , '''23''' (1971) pp. 313–333 {{MR|0287477}} {{ZBL|}} </td></tr><tr><td valign="top">[a23]</td> <td valign="top"> S. Tanno, "On the isometry of Sasakian manifolds" ''J. Math. Soc. Japan'' , '''22''' (1970) pp. 579–590 {{MR|271874}} {{ZBL|0197.48004}} </td></tr></table> |
Revision as of 15:30, 1 July 2020
Sasakian and $3$-Sasakian spaces are odd-dimensional companions of Kähler and hyper-Kähler manifolds, respectively. A Riemannian manifold $( \mathcal{S} , g )$ of dimension $m$ is called Sasakian if the holonomy group of the metric cone $( C ( \mathcal{S} ) , \overline { g } ) = ( \mathbf{R} _ { + } \times \mathcal{S} , d r ^ { 2 } + r ^ { 2 } g )$ reduces to a subgroup of $U ( ( m + 1 ) / 2 )$. In particular, $m = 2l + 1$, $l \geq 1$, and such a cone is a Kähler manifold. Let $I$ be a complex structure on $C ( \mathcal S )$. Then $\xi = I ( \partial _ { r } )$ restricted to $\mathcal{S}$ is a unit Killing vector field (cf. also Killing vector) with the property that the sectional curvature of every section containing $\xi $ equals one. Such a $\xi $ is called the characteristic vector field on $\mathcal{S}$ and its properties can be used as an alternative characterization of a Sasakian manifold.
Similarly, one says that $( \mathcal{S} , g )$ is a $3$-Sasakian manifold if the holonomy group of the metric cone $( C ( \mathcal{S} ) , \overline { g } )$ reduces to a subgroup of $\operatorname { Sp } ( ( m + 1 ) / 4 )$. In particular, $m = 4 n + 3$, $n \geq 1$, and the cone is a hyper-Kähler manifold. When $\mathcal{S}$ is $3$-Sasakian, the hyper-Kähler structure on the associated cone $C ( \mathcal S )$ can be used to define three vector fields $\xi ^ {a } = I ^ { a} ( \partial _ { r } )$, $a = 1,2,3$, where $\{ I ^ { 1 } , I ^ { 2 } , I ^ { 3 } \}$ is a hypercomplex structure on $C ( \mathcal S )$. It follows that, when restricted to $\mathcal{S}$, $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ are Killing vector fields such that $g ( \xi ^ { a } , \xi ^ { b } ) = \delta _ { a b }$ and $[ \xi ^ {a } , \xi ^ { b } ] = 2 \epsilon _ { a b c } \xi ^ { c }$. Hence, they are orthonormal and locally define an isometric $ \operatorname {SO} ( 3 )$ (or $\operatorname{SU} ( 2 )$) action on $\mathcal{S}$. In turn, the triple $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ yields $\eta ^ { a } ( Y ) = g ( \xi ^ { a } , Y )$ and $\Phi ^ { a } ( Y ) = \nabla _ { Y } \xi ^ { a }$ for each $a = 1,2,3$. The collection of tensors $\{ \xi ^ { a } , \eta ^ { a } , \Phi ^ { a } \}_{a = 1,2,3}$ is traditionally called the $3$-Sasakian structure on $( \mathcal{S} , g )$. This is the way such structures were first introduced in the work of C. Udrişte [a1] and Y. Kuo [a2] in 1969 and 1970.
Every $3$-Sasakian manifold is an Einstein manifold with positive Einstein constant $\lambda = \operatorname { dim } ( \mathcal{S} ) - 1$. If $\mathcal{S}$ is complete, it is compact with finite fundamental group. If $( \mathcal{S} , g )$ is compact, the characteristic vector fields $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ are complete and define a $3$-dimensional foliation $\mathcal{F} _ { 3 }$ on $\mathcal{S}$. The leaves of this foliation are necessarily compact, since $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ defines a locally free $\operatorname{SU} ( 2 )$ action on $\mathcal{S}$. Hence, the foliation $\mathcal{F} _ { 3 }$ is automatically almost-regular and the space of leaves is a compact orbifold, denoted by $\mathcal{O}$. The leaves of $\mathcal{F} _ { 3 }$ are totally geodesic submanifolds of constant sectional curvature equal one (cf. also Totally-geodesic manifold). They are all $3$-dimensional homogeneous spherical space forms $S ^ { 3 } / \Gamma$, where $\Gamma \subset \operatorname{SU} ( 2 )$ is a finite subgroup (cf. also Space forms). In particular, the leaves are $3$-Sasakian manifolds themselves. The space of leaves $\mathcal{O}$ is a compact positive quaternion Kähler orbifold. The principal leaves are always diffeomorphic to either $S ^ { 3 }$ or $ \operatorname {SO} ( 3 )$. A compact $3$-Sasakian manifold is said to be regular if $\mathcal{F} _ { 3 }$ is regular, i.e., if all the leaves are diffeomorphic. In this case $\mathcal{O}$ is a smooth manifold (cf. Differentiable manifold). For any $\tau = ( \tau _ { 1 } , \tau _ { 2 } , \tau _ { 3 } ) \in \mathbf{R} ^ { 3 }$ such that $\tau _ { 1 } ^ { 2 } + \tau _ { 3 } ^ { 2 } + \tau _ { 3 } ^ { 2 } = 1$, the vector field $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$ has the Sasakian property. Hence, a $3$-Sasakian manifold has a $2$-sphere worth of Sasakian structures (just as hyper-Kähler manifold has an $S ^ { 2 }$-worth of complex structures). When $\mathcal{S}$ is compact, the vector field $\xi ( \tau )$ defines a $1$-dimensional foliation $\mathcal{F} _ { \tau } \subset \mathcal{F} _ { 3 } \subset \mathcal{S}$ with compact leaves. Such a foliation gives $\mathcal{S}$ an isometric locally free circle action $U ( 1 ) _ { \tau } \subset \operatorname { SU } ( 2 )$. The space of leaves $\mathcal{Z} = \mathcal{S} / \mathcal{F} _ { \tau }$ is a compact Kähler–Einstein orbifold of positive scalar curvature. It is a simply-connected normal projective algebraic variety (cf. Projective algebraic set). $\mathcal Z$ has a complex contact structure and it is a $\mathbf{Q}$-factorial Fano variety (cf. also Fano variety). It is an orbifold twistor space of $\mathcal{O}$. All the foliations associated to $\mathcal{S}$ can be described in the the following diagram 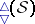 of orbifold fibrations:
of orbifold fibrations:
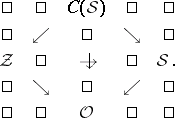 |
All four geometries in the above diagram are Einstein. Both $\mathcal{S}$ and $\mathcal Z$ admit second, non-isometric Einstein metrics of positive scalar curvature. Every $3$-Sasakian manifold is a spin manifold (cf. Spinor structure). When $\mathcal{S}$ is complete, simply-connected and not of constant curvature, it admits $n + 2$ Killing spinors, where $\operatorname { dim } ( {\cal S} ) = 4 n + 3$. The holonomy group of $\mathcal{S}$ never reduces to a proper subgroup of $\operatorname{SO} ( 4 n + 3 )$ and the metric admits no infinitesimal deformations.
For every compact semi-simple Lie group $G$ one has a corresponding diagram $^{ \bigtriangleup } _ { \bigtriangledown } ( G / K )$ with ${\cal O} = G / \operatorname { Sp } ( 1 ) . K$ being a symmetric positive quaternion Kähler manifold (a Wolf space) and $\mathcal{Z} = G / U ( 1 ) . K$. In particular, every every $3$-Sasakian $G$-homogeneous space is regular and it is one of the spaces
\begin{equation*} \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times \mathbf{Z} _ { 2 }, \end{equation*}
\begin{equation*} \operatorname {SU} ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , \operatorname {SO} ( k ) / \operatorname {SO} ( k - 4 ) \times \operatorname {Sp} ( 1 ), \end{equation*}
\begin{equation*} G _ { 2 } / \operatorname { Sp } ( 1 ) , \quad F _ { 4 } / \operatorname { Sp } ( 3 ) , E _ { 6 } / \operatorname{SU} ( 6 ) , \quad E _ { 7 } / \operatorname { Spin } ( 12 ) , \quad E _ { 8 } / E _ { 7 }. \end{equation*}
Here, $n \geq 0$, $\operatorname{Sp} ( 0 )$ denotes the trivial group, $m > 3$, and $k \geq 7$. Hence, there is one-to-one correspondence between the simple Lie algebras and the simply-connected $3$-Sasakian homogeneous manifolds.
There is a conjecture that all complete regular $3$-Sasakian manifolds are homogeneous. It is a simple translation of the corresponding conjecture due to C. LeBrun and S. Salamon [a3] that all positive quaternion Kähler manifolds are symmetric. This is known to be true when $\operatorname { dim } ( {\cal S} ) = 7$ or $11$ ($\operatorname { dim } ( \mathcal{O} ) = 4$ or $8$). More generally, it is know that in each dimension $4 n + 3$, there are only finitely many complete regular $3$-Sasakian manifolds, all of them having $b _ { 2 } ( \mathcal{S} ) \leq 1$ with equality holding only when $\mathcal{S} = \text{SU} ( m ) / S ( U ( m - 2 ) \times U ( 1 ) )$. Furthermore, it was shown by K. Galicki and S. Salamon [a4] that each Betti number of such an $\mathcal{S}$ must satisfy the linear relation
\begin{equation*} \sum _ { k = 1 } ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0 \end{equation*}
with odd Betti numbers $b _ { 2i + 1} ( \mathcal{S} ) = 0$ for $ { i } \leq n$. In fact the vanishing of odd Betti numbers holds true in the irregular case as well. There are, however, examples of an $11$-dimensional irregular $3$-Sasakian manifold for which $b _ { 2 } \neq b _ { 4 }$ and of $15$-dimensional manifolds with $b _ { 2 } \neq b _ { 6 }$. These were constructed explicitly by C. Boyer, K. Galicki and B. Mann [a5].
The first complete irregular examples that are not quotients of homogeneous spaces by a discrete group of isometries were obtained also by Boyer, Galicki and Mann [a10], [a11], [a12], [a13], [a14], [a15], using a method called $3$-Sasakian reduction. The examples are bi-quotients of unitary groups of the form $\mathcal{S} ( p ) = U ( 1 ) _ { p } \backslash U ( n + 2 ) / U ( n )$. The $( 4 n + 3 )$-dimensional family ${\cal S} ( \operatorname{p} )$ depends on positive integral "weights" $\operatorname{p} = ( p _ { 1 } , \dots , p _ { n + 2} )$ which are pairwise relatively prime. The integral cohomology ring of ${\cal S} ( \operatorname{p} )$ depends on the weight vector $\text{p}$ and one gets infinitely many homotopy types of compact simply-connected $3$-Sasakian manifolds in each allowable dimension $\geq 7$. Other irregular examples were constructed later in dimension $7$, $11$, $15$ by Boyer, Galicki, Mann, and E. Rees [a6]. The same method of $3$-Sasakian reduction was used to obtain families of compact simply-connected $3$-Sasakian $7$-manifolds with an arbitrary second Betti number. All these examples are toric, i.e., having $T ^ { 2 } \times \operatorname { Sp } ( 1 )$ or $T ^ { 2 } \times SO ( 3 )$ as the group of isometries with the $2$-torus action preserving the $3$-Sasakian structure. R. Bielawski [a7] showed that, in any dimension $4 n + 3$, a toric $3$-Sasakian manifold is necessarily diffeomorphic to one of the quotients obtained in [a6]. Examples of compact $3$-Sasakian manifold which are not toric can also be constructed.
After their introduction in 1969, $3$-Sasakian manifolds were vigorously studied by a group of Japanese geometers, including S. Ishihara, T. Kashiwada, M. Konishi, Y. Kuo, S. Tachibana, S. Tanno, and W.N. Yu [a16], [a17], [a18], [a19], [a20], [a21], [a22], [a23]. This lasted until 1975, when the whole subject was relegated to an almost complete obscurity largely due to lack of any interesting examples. In the early 1990s $3$-Sasakian manifolds returned in two different areas. One of them is the study of $7$-manifolds admitting Killing spinors, in the work of T. Friedrich and I. Kath [a8]. The other is the work [a10], [a11], [a12], [a13], [a14], [a15], of Boyer–Galicki–Mann, in which the first irregular examples are constructed and a systematic study of geometry and topology of compact $3$-Sasakian manifolds is undertaken.
For a detailed review of the subject and extensive bibliography see [a9].
References
| [a1] | C. Udrişte, "Structures presque coquaternioniennes" Bull. Math. Soc. Sci. Math. Roum. , 12 (1969) pp. 487–507 MR0296849 Zbl 0213.48205 |
| [a2] | Y.-Y. Kuo, "On almost contact 3-structure" Tôhoku Math. J. , 22 (1970) pp. 325–332 MR0278225 Zbl 0205.25801 |
| [a3] | K. Galicki, S. Salamon, "On Betti numbers of 3-Sasakian manifolds" Geom. Dedicata , 63 (1996) pp. 45–68 MR1413621 |
| [a4] | C. LeBrun, S.M. Salamon, "Strong rigidity of positive quaternion–Kähler manifolds" Invent. Math. , 118 (1994) pp. 109–132 |
| [a5] | C.P. Boyer, K. Galicki, B.M. Mann, "A note on smooth toral reductions of spheres" Manuscripta Math. , 95 (1998) pp. 149–158 MR1603301 Zbl 0913.53020 |
| [a6] | C.P. Boyer, K. Galicki, B.M. Mann, E. Rees, "Compact 3-Sasakian 7-manifolds with arbitrary second Betti number" Invent. Math. , 131 (1998) pp. 321–344 MR1608567 Zbl 0901.53033 |
| [a7] | R. Bielawski, "Complete $T ^ { n }$-invariant hyperkähler $4 n$-manifolds" MPI preprint , 65 (1998) (www.mpim-bonn.mpg.de/html/preprints/preprints.html) |
| [a8] | T. Friedrich, I. Kath, "Compact seven-dimensional manifolds with Killing spinors" Comm. Math. Phys. , 133 (1990) pp. 543–561 |
| [a9] | C.P. Boyer, K. Galicki, "3-Sasakian Manifolds" C. LeBrun (ed.) M. Wang (ed.) , Essays on Einstein Manifolds , Internat. Press (to appear) MR1798609 MR1645769 MR1433200 MR1293878 MR1249451 Zbl 1008.53047 Zbl 0942.53030 Zbl 0901.53033 Zbl 0889.53029 Zbl 0814.53037 |
| [a10] | C.P. Boyer, K. Galicki, B.M. Mann, "Quaternionic reduction and Einstein manifolds" Commun. Anal. Geom. , 1 (1993) pp. 1–51 MR1243524 Zbl 0856.53038 |
| [a11] | C.P. Boyer, K. Galicki, B.M. Mann, "The geometry and topology of 3-Sasakian manifolds" J. Reine Angew. Math. , 455 (1994) pp. 183–220 MR1293878 Zbl 0889.53029 |
| [a12] | C.P. Boyer, K. Galicki, B.M. Mann, "New examples of inhomogeneous Einstein manifolds of positive scalar curvature" Math. Res. Lett. , 1 (1994) pp. 115–121 MR1258497 Zbl 0842.53033 |
| [a13] | C.P. Boyer, K. Galicki, B.M. Mann, "3-Sasakian manifolds" Proc. Japan Acad. Ser. A , 69 (1993) pp. 335–340 MR1249451 Zbl 0814.53037 |
| [a14] | C.P. Boyer, K. Galicki, B.M. Mann, "Hypercomplex structures on Stiefel manifolds" Ann. Global Anal. Geom. , 14 (1996) pp. 81–105 MR1375068 Zbl 0843.53030 |
| [a15] | C.P. Boyer, K. Galicki, B.M. Mann, "New examples of inhomogeneous Einstein manifolds of positive scalar curvature" Bull. London Math. Soc. , 28 (1996) pp. 401–408 MR1258497 Zbl 0842.53033 |
| [a16] | S. Ishihara, M. Konishi, "Fibered Riemannian spaces with Sasakian 3-structure" , Differential Geometry, in Honor of K. Yano , Kinokuniya (1972) pp. 179–194 |
| [a17] | S. Ishihara, "Quaternion Kählerian manifolds and fibered Riemannian spaces with Sasakian 3-structure" Kodai Math. Sem. Rep. , 25 (1973) pp. 321–329 |
| [a18] | T. Kashiwada, "A note on a Riemannian space with Sasakian 3-structure" Nat. Sci. Rep. Ochanomizu Univ. , 22 (1971) pp. 1–2 MR0303449 Zbl 0228.53033 |
| [a19] | M. Konishi, "On manifolds with Sasakian 3-structure over quaternion Kählerian manifolds" Kodai Math. Sem. Rep. , 26 (1975) pp. 194–200 |
| [a20] | Y.-Y. Kuo, S. Tachibana, "On the distribution appeared in contact 3-structure" Taita J. Math. , 2 (1970) pp. 17–24 MR0309004 Zbl 0231.53053 |
| [a21] | S. Tachibana, W.N. Yu, "On a Riemannian space admitting more than one Sasakian structure" Tôhoku Math. J. , 22 (1970) pp. 536–540 MR0275329 |
| [a22] | S. Tanno, "Killing vectors on contact Riemannian manifolds and fiberings related to the Hopf fibrations" Tôhoku Math. J. , 23 (1971) pp. 313–333 MR0287477 |
| [a23] | S. Tanno, "On the isometry of Sasakian manifolds" J. Math. Soc. Japan , 22 (1970) pp. 579–590 MR271874 Zbl 0197.48004 |
3-Sasakian manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=3-Sasakian_manifold&oldid=49907