Difference between revisions of "Boolean circuit"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 87 formulas out of 90 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 90 formulas, 87 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | An $n$-ary Boolean function $f ( x _ { 1 } , \ldots , x _ { n } )$ is a function from $\{ 0,1 \} ^ { n }$ with values in $\{ 0,1 \}$. The values $0$, $1$ are called Boolean values, or bits, or truth values if they are identified with false and true (cf. also [[Boolean function|Boolean function]]). Elements of $\{ 0,1 \} ^ { n }$ are Boolean strings of length $n$ (or bit strings). $B _ { n }$ is the set of all $2 ^ { 2 ^ { n } }$ $n$-ary Boolean functions. | ||
| − | + | A basis of connectives is any non-empty set $\Omega$ of Boolean functions, not necessarily of the same arity. An $\Omega$-formula for $f ( x _ { 1 } , \ldots , x _ { n } )$ is a formula built from Boolean variables $x _ { 1 } , \ldots , x _ { n }$ using connectives from $\Omega$. A basis $\Omega$ is complete if all Boolean functions are definable by an $\Omega$-formula. Examples of complete bases are: $B _ { 2 }$, the set of all binary Boolean functions, or the DeMorgan basis $\{ 0,1 , \neg , \vee , \wedge \}$. | |
| − | + | A more general way to define (equivalently, compute) Boolean functions is by circuits (straight line programs) that are simplified mathematical models of integrated circuits. A Boolean circuit over a basis $\Omega$ for $f \in B _ { n }$ is a sequence $g _ { 1 } , \ldots , g _ { k }$ of functions from $B _ { n }$ such that $g _ { k } = f$ and such that any $g_i$ is either one of the projections $x _ { 1 } , \ldots , x _ { n }$ or is equal to $h ( g _ { j _ { 1 } } , \dots , g _ { j _ { r } } )$, for some $h \in \Omega$ and $j_1 , \ldots , j _ { r } < i$. Drawing directed edges from all such $j _ { 1 } , \dots , j _ { r }$ to $i$, and labelling $i$ by $h$, defines a labelled directed acyclic graph (cf. also [[Graph, oriented|Graph, oriented]]). The size of the circuit is $k$. The maximum length of a path from a vertex corresponding to one of the inputs $x _ { 1 } , \ldots , x _ { n }$ to $g_{k}$ is the depth of the circuit. Note that formulas are circuits whose graphs are trees. | |
| − | the | + | There are three basic ways to measure the complexity of a Boolean function, given a basis $\Omega$: |
| − | the minimum | + | the minimum size $L _ { \Omega } ( f )$ of an $\Omega$-formula defining $f$, |
| − | + | the minimum size $C _ { \Omega } ( f )$ of a circuit over $\Omega$ defining $f$, and | |
| − | + | the minimum depth $D _ { \Omega } ( f )$ of a circuit over $\Omega$ defining $f$. For two complete bases $\Omega$, $\Omega ^ { \prime }$, the measures $C _ { \Omega } ( f )$, $C _ { \Omega ^ { \prime } } ( f )$ and $D _ { \Omega } ( f )$, $D _ { \Omega ^ { \prime } } ( f )$ are proportional to each other, and $L _ { \Omega } ( f )$, $L _ { \Omega ^ { \prime } } ( f )$ are polynomially related. A relation exists between the formula size and the circuit depth (see [[#References|[a13]]]): $\operatorname { log } ( L _ { \Omega } ( f ) )$ and $D _ { \Omega } ( f )$ are proportional to each other, provided $\Omega$ is finite. | |
| − | + | By estimating the number of circuits of a bounded size, C.E. Shannon [[#References|[a11]]] proved (cf. [[#References|[a14]]] for an optimal computation) that for almost-all $f \in B _ { n }$, $C _ { B _ { 2 } } ( f ) \geq 2 ^ { n } / n$. On the other hand, | |
| − | + | \begin{equation*} C _ { B _ { 2 } } ( f ) \leq \frac { 2 ^ { n } } { n } ( 1 + o ( 1 ) ), \end{equation*} | |
| − | + | for all $f \in B _ { n }$, see [[#References|[a8]]]. | |
| − | Interesting upper bounds are also known: a DeMorgan circuit of size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120370/b12037088.png" /> for multiplication of two | + | For a [[Formal language|formal language]] $L \subseteq \{ 0,1 \}^*$, let $L_{n}$ be the characteristic function of $L \cap \{ 0,1 \} ^ { n }$. The main open problem in Boolean complexity theory (cf. [[#References|[a4]]]) is whether there is a language $L$ accepted by a non-deterministic polynomial-time Turing machine (cf. also [[Turing machine|Turing machine]]) such that $C _ { \Omega } ( L _ { n } )$ is not bounded by any polynomial in $n$. The importance of this question stems from the fact that the affirmative answer implies that the computational complexity classes $\mathcal{P}$ and $\cal N P$ are different, as $C _ { B _ { 2 } } ( L _ { n } )$ is bounded by a polynomial for any $L$ decidable in polynomial time (cf. [[#References|[a10]]] and also [[NP|$\cal N P$]]). |
| + | |||
| + | No super-linear lower bounds on $C _ { B _ { 2 } } ( L _ { n } )$ are known for any $L \in \mathcal{N} \mathcal{P}$. However, if additional restrictions are put on the circuits, then strong lower bounds are known. Most notable are two results: any circuit of depth $d \geq 2$ over a DeMorgan-like basis $\{ 0,1 , \neg , \vee , \wedge \}$, allowing $\vee , \wedge$ of unbounded arity, computing the parity function $\oplus _ { n }$ must have size at least $\operatorname { exp } ( \Omega ( n ^ { 1 / d - 1 } ) )$ (see [[#References|[a1]]], [[#References|[a5]]], [[#References|[a15]]], [[#References|[a6]]]), and any circuit in the monotone basis $\{ 0,1 , \vee , \wedge \}$ computing whether or not a graph on $n$ vertices contains a clique of size at least $k \leq n ^ { 1 / 4 }$ must have size at least $n ^ { \Omega ( \sqrt { k } ) }$ (see [[#References|[a9]]], [[#References|[a3]]]). | ||
| + | |||
| + | Interesting upper bounds are also known: a DeMorgan circuit of size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120370/b12037088.png"/> for multiplication of two $n$-bit long numbers, [[#References|[a12]]] (it is still open (1998) if there are linear size circuits), and a monotone DeMorgan sorting network of simultaneous size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120370/b12037090.png"/> and depth $O( \operatorname { log } n )$, see [[#References|[a2]]]. | ||
Various parts of computational complexity (cf. also [[Complexity theory|Complexity theory]]) are directly related to lower-bound problems for Boolean functions; for example, communication complexity, cf. [[#References|[a7]]]. | Various parts of computational complexity (cf. also [[Complexity theory|Complexity theory]]) are directly related to lower-bound problems for Boolean functions; for example, communication complexity, cf. [[#References|[a7]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> M. Ajtai, "$\sum _ { 1 } ^ { 1 }$ - formulae on finite structures" ''Ann. Pure Appl. Logic'' , '''24''' (1983) pp. 1–48</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> M. Ajtai, J. Komlós, E. Szemerédi, "An <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120370/b12037093.png"/> sorting network" ''Combinatorica'' , '''3''' (1983) pp. 1–19</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> N. Alon, R. Boppana, "The monotone circuit complexity of Boolean functions" ''Combinatorica'' , '''7''' : 1 (1987) pp. 1–22</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> R. Boppana, M. Sipser, "Complexity of finite functions" J. van Leeuwen (ed.) , ''Handbook of Theoretical Computer Science'' , '''A''' (1990) pp. 758–804; Chap.14</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> M. Furst, J.B. Saxe, M. Sipser, "Parity, circuits and the polynomial-time hierarchy" ''Math. Systems Theory'' , '''17''' (1984) pp. 13–27</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> J. Hastad, "Almost optimal lower bounds for small depth circuits" S. Micali (ed.) , ''Randomness and Computation'' , ''Adv. Comput. Res.'' , '''5''' , JAI Press (1989) pp. 143–170</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> E. Kushilevitz, N. Nisan, "Communication complexity" , Cambridge Univ. Press (1996)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> O.B. Lupanov, "A method of circuit synthesis" ''Izv. V.U.Z. (Radiofizika)'' , '''1''' : 1 (1958) pp. 120–140 (In Russian)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> A.A. Razborov, "Lower bounds on the monotone complexity of some Boolean functions" ''Soviet Math. Dokl.'' , '''31''' (1985) pp. 354–357</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> J.E. Savage, "Computational work and time on finite machines" ''J. ACM'' , '''19''' : 4 (1972) pp. 660–674</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> C.E. Shannon, "The synthesis of two-terminal switching circuits" ''Bell Systems Techn. J.'' , '''28''' : 1 (1949) pp. 59–98</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> A. Schonhage, V. Strassen, "Schnelle Multiplikation grosser Zahlen" ''Computing'' , '''7''' (1971) pp. 281–292</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> P.M. Spira, "On time-hardware complexity of tradeoffs for Boolean functions" , ''Proc. 4th Hawaii Symp. System Sciences'' , North Hollywood&Western Periodicals (1971) pp. 525–527</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> I. Wegener, "The complexity of Boolean functions" , Wiley&Teubner (1987)</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> Y. Yao, "Separating the polynomial-time hierarchy by oracles" , ''Proc. 26th Ann. IEEE Symp. Found. Comput. Sci.'' (1985) pp. 1–10</td></tr></table> |
Revision as of 15:30, 1 July 2020
An $n$-ary Boolean function $f ( x _ { 1 } , \ldots , x _ { n } )$ is a function from $\{ 0,1 \} ^ { n }$ with values in $\{ 0,1 \}$. The values $0$, $1$ are called Boolean values, or bits, or truth values if they are identified with false and true (cf. also Boolean function). Elements of $\{ 0,1 \} ^ { n }$ are Boolean strings of length $n$ (or bit strings). $B _ { n }$ is the set of all $2 ^ { 2 ^ { n } }$ $n$-ary Boolean functions.
A basis of connectives is any non-empty set $\Omega$ of Boolean functions, not necessarily of the same arity. An $\Omega$-formula for $f ( x _ { 1 } , \ldots , x _ { n } )$ is a formula built from Boolean variables $x _ { 1 } , \ldots , x _ { n }$ using connectives from $\Omega$. A basis $\Omega$ is complete if all Boolean functions are definable by an $\Omega$-formula. Examples of complete bases are: $B _ { 2 }$, the set of all binary Boolean functions, or the DeMorgan basis $\{ 0,1 , \neg , \vee , \wedge \}$.
A more general way to define (equivalently, compute) Boolean functions is by circuits (straight line programs) that are simplified mathematical models of integrated circuits. A Boolean circuit over a basis $\Omega$ for $f \in B _ { n }$ is a sequence $g _ { 1 } , \ldots , g _ { k }$ of functions from $B _ { n }$ such that $g _ { k } = f$ and such that any $g_i$ is either one of the projections $x _ { 1 } , \ldots , x _ { n }$ or is equal to $h ( g _ { j _ { 1 } } , \dots , g _ { j _ { r } } )$, for some $h \in \Omega$ and $j_1 , \ldots , j _ { r } < i$. Drawing directed edges from all such $j _ { 1 } , \dots , j _ { r }$ to $i$, and labelling $i$ by $h$, defines a labelled directed acyclic graph (cf. also Graph, oriented). The size of the circuit is $k$. The maximum length of a path from a vertex corresponding to one of the inputs $x _ { 1 } , \ldots , x _ { n }$ to $g_{k}$ is the depth of the circuit. Note that formulas are circuits whose graphs are trees.
There are three basic ways to measure the complexity of a Boolean function, given a basis $\Omega$:
the minimum size $L _ { \Omega } ( f )$ of an $\Omega$-formula defining $f$,
the minimum size $C _ { \Omega } ( f )$ of a circuit over $\Omega$ defining $f$, and
the minimum depth $D _ { \Omega } ( f )$ of a circuit over $\Omega$ defining $f$. For two complete bases $\Omega$, $\Omega ^ { \prime }$, the measures $C _ { \Omega } ( f )$, $C _ { \Omega ^ { \prime } } ( f )$ and $D _ { \Omega } ( f )$, $D _ { \Omega ^ { \prime } } ( f )$ are proportional to each other, and $L _ { \Omega } ( f )$, $L _ { \Omega ^ { \prime } } ( f )$ are polynomially related. A relation exists between the formula size and the circuit depth (see [a13]): $\operatorname { log } ( L _ { \Omega } ( f ) )$ and $D _ { \Omega } ( f )$ are proportional to each other, provided $\Omega$ is finite.
By estimating the number of circuits of a bounded size, C.E. Shannon [a11] proved (cf. [a14] for an optimal computation) that for almost-all $f \in B _ { n }$, $C _ { B _ { 2 } } ( f ) \geq 2 ^ { n } / n$. On the other hand,
\begin{equation*} C _ { B _ { 2 } } ( f ) \leq \frac { 2 ^ { n } } { n } ( 1 + o ( 1 ) ), \end{equation*}
for all $f \in B _ { n }$, see [a8].
For a formal language $L \subseteq \{ 0,1 \}^*$, let $L_{n}$ be the characteristic function of $L \cap \{ 0,1 \} ^ { n }$. The main open problem in Boolean complexity theory (cf. [a4]) is whether there is a language $L$ accepted by a non-deterministic polynomial-time Turing machine (cf. also Turing machine) such that $C _ { \Omega } ( L _ { n } )$ is not bounded by any polynomial in $n$. The importance of this question stems from the fact that the affirmative answer implies that the computational complexity classes $\mathcal{P}$ and $\cal N P$ are different, as $C _ { B _ { 2 } } ( L _ { n } )$ is bounded by a polynomial for any $L$ decidable in polynomial time (cf. [a10] and also $\cal N P$).
No super-linear lower bounds on $C _ { B _ { 2 } } ( L _ { n } )$ are known for any $L \in \mathcal{N} \mathcal{P}$. However, if additional restrictions are put on the circuits, then strong lower bounds are known. Most notable are two results: any circuit of depth $d \geq 2$ over a DeMorgan-like basis $\{ 0,1 , \neg , \vee , \wedge \}$, allowing $\vee , \wedge$ of unbounded arity, computing the parity function $\oplus _ { n }$ must have size at least $\operatorname { exp } ( \Omega ( n ^ { 1 / d - 1 } ) )$ (see [a1], [a5], [a15], [a6]), and any circuit in the monotone basis $\{ 0,1 , \vee , \wedge \}$ computing whether or not a graph on $n$ vertices contains a clique of size at least $k \leq n ^ { 1 / 4 }$ must have size at least $n ^ { \Omega ( \sqrt { k } ) }$ (see [a9], [a3]).
Interesting upper bounds are also known: a DeMorgan circuit of size 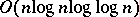 for multiplication of two $n$-bit long numbers, [a12] (it is still open (1998) if there are linear size circuits), and a monotone DeMorgan sorting network of simultaneous size
for multiplication of two $n$-bit long numbers, [a12] (it is still open (1998) if there are linear size circuits), and a monotone DeMorgan sorting network of simultaneous size 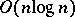 and depth $O( \operatorname { log } n )$, see [a2].
and depth $O( \operatorname { log } n )$, see [a2].
Various parts of computational complexity (cf. also Complexity theory) are directly related to lower-bound problems for Boolean functions; for example, communication complexity, cf. [a7].
References
| [a1] | M. Ajtai, "$\sum _ { 1 } ^ { 1 }$ - formulae on finite structures" Ann. Pure Appl. Logic , 24 (1983) pp. 1–48 |
| [a2] | M. Ajtai, J. Komlós, E. Szemerédi, "An 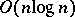 sorting network" Combinatorica , 3 (1983) pp. 1–19 sorting network" Combinatorica , 3 (1983) pp. 1–19 |
| [a3] | N. Alon, R. Boppana, "The monotone circuit complexity of Boolean functions" Combinatorica , 7 : 1 (1987) pp. 1–22 |
| [a4] | R. Boppana, M. Sipser, "Complexity of finite functions" J. van Leeuwen (ed.) , Handbook of Theoretical Computer Science , A (1990) pp. 758–804; Chap.14 |
| [a5] | M. Furst, J.B. Saxe, M. Sipser, "Parity, circuits and the polynomial-time hierarchy" Math. Systems Theory , 17 (1984) pp. 13–27 |
| [a6] | J. Hastad, "Almost optimal lower bounds for small depth circuits" S. Micali (ed.) , Randomness and Computation , Adv. Comput. Res. , 5 , JAI Press (1989) pp. 143–170 |
| [a7] | E. Kushilevitz, N. Nisan, "Communication complexity" , Cambridge Univ. Press (1996) |
| [a8] | O.B. Lupanov, "A method of circuit synthesis" Izv. V.U.Z. (Radiofizika) , 1 : 1 (1958) pp. 120–140 (In Russian) |
| [a9] | A.A. Razborov, "Lower bounds on the monotone complexity of some Boolean functions" Soviet Math. Dokl. , 31 (1985) pp. 354–357 |
| [a10] | J.E. Savage, "Computational work and time on finite machines" J. ACM , 19 : 4 (1972) pp. 660–674 |
| [a11] | C.E. Shannon, "The synthesis of two-terminal switching circuits" Bell Systems Techn. J. , 28 : 1 (1949) pp. 59–98 |
| [a12] | A. Schonhage, V. Strassen, "Schnelle Multiplikation grosser Zahlen" Computing , 7 (1971) pp. 281–292 |
| [a13] | P.M. Spira, "On time-hardware complexity of tradeoffs for Boolean functions" , Proc. 4th Hawaii Symp. System Sciences , North Hollywood&Western Periodicals (1971) pp. 525–527 |
| [a14] | I. Wegener, "The complexity of Boolean functions" , Wiley&Teubner (1987) |
| [a15] | Y. Yao, "Separating the polynomial-time hierarchy by oracles" , Proc. 26th Ann. IEEE Symp. Found. Comput. Sci. (1985) pp. 1–10 |
Boolean circuit. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boolean_circuit&oldid=49903