Difference between revisions of "Weil-Petersson metric"
Ulf Rehmann (talk | contribs) m (moved Weil–Petersson metric to Weil-Petersson metric: ascii title) |
m (AUTOMATIC EDIT (latexlist): Replaced 40 formulas out of 42 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 42 formulas, 40 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A. Weil introduced a [[Kähler metric|Kähler metric]] for the [[Teichmüller space|Teichmüller space]] $T _ { g , n }$, the space of homotopy-marked Riemann surfaces (cf. [[Riemann surface|Riemann surface]]) of genus $g$ with $n$ punctures and negative [[Euler characteristic|Euler characteristic]], [[#References|[a1]]]. The cotangent space at a marked Riemann surface $\{ R \}$ (the space $Q ( R )$ of holomorphic quadratic differentials on $R$; cf. also [[Quadratic differential|Quadratic differential]]) is considered with the Petersson Hermitian pairing. The Weil–Petersson metric calibrates the variations of the complex structure of $\{ R \}$. The uniformization theorem implies that for a surface of negative Euler characteristic, the following two determinations are equivalent: a complex structure and a complete hyperbolic metric. Accordingly, the Weil–Petersson metric has been studied through [[Quasi-conformal mapping|quasi-conformal mapping]], solution of the inhomogeneous $\overline { \partial }$-equation (cf. also [[Neumann d-bar problem|Neumann $\overline { \partial }$-problem]]), the prescribed curvature equation, and global analysis, [[#References|[a1]]], [[#References|[a7]]], [[#References|[a10]]]. | ||
| − | The | + | The quotient of the Teichmüller space $\mathcal{T}_{g,n} $ by the action of the mapping class group is the moduli space of Riemann surfaces ${\cal M} _ { g , n }$ (cf. also [[Moduli of a Riemann surface|Moduli of a Riemann surface]]; [[Moduli theory|Moduli theory]]); the Weil–Petersson metric is a mapping class group invariant and descends to ${\cal M} _ { g , n }$. $\overline { \mathcal{M}_ { g , n } }$ (the stable-curve compactification of ${\cal M} _ { g , n }$) is a projective variety with $\mathcal{D} _ { g , n } = \overline { \mathcal{M} _ { g , n } } - \mathcal{M} _ { g , n }$ (the divisor of noded stable-curves, i.e. the Riemann surfaces "with disjoint simple loops collapsed to points" and each component of the nodal-complement having negative Euler characteristic). Expansions for the Weil–Petersson metric in a neighbourhood of $\mathcal{D} _ { g , n }$ provide that the metric on ${\cal M} _ { g , n }$ is not complete and that there is a distance completion separating points on $\overline { \mathcal{M}_ { g , n } }$, [[#References|[a6]]]. |
| − | + | The Weil–Petersson metric has negative sectional curvature, [[#References|[a9]]], [[#References|[a12]]]. The behaviour near $\mathcal{D} _ { g , n }$ shows that the sectional curvature has as infimum negative infinity and as supremum zero. The holomorphic sectional, Ricci and scalar curvatures are each bounded above by genus-dependent negative constants. A modification of the metric introduced by C.T. McMullen [[#References|[a5]]] is Kähler-hyperbolic in the sense of M. Gromov (cf. also [[Gromov hyperbolic space|Gromov hyperbolic space]]), has positive first eigenvalue and provides that the sign of the ${\cal M} _ { g , n }$ orbifold Euler characteristic is given by the parity of the dimension. | |
| − | The | + | The Weil–Petersson Kähler form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130060/w13006022.png"/> appears in several contexts. L.A. Takhtayan and P.G. Zograf [[#References|[a8]]] considered the local index theorem for families of $\overline { \partial }$-operators and calculated the first Chern form of the determinant line bundle $\operatorname{det} \; \operatorname{ind} \overline { \partial }$ using Quillen's construction of a metric based on the hyperbolic metric; the Chern form is |
| − | + | \begin{equation*} \frac { 1 } { 12 \pi ^ { 2 } } \omega _{\text{WP}}. \end{equation*} | |
| − | [[#References|[a14]]]. This result is the basis for a proof of the projectivity of | + | The "universal curve" is the fibration $\mathcal{C} _ { g ,\, n }$ over $\mathcal{T}_{g,n} $ with fibre $R$ above the class $\{ R \}$. The uniformization theorem provides a metric for the vertical line bundle ${\cal V} _ { g , n }$ of the fibration. The setup extends to the compactification: The pushdown of the square of the first Chern form of $\overline { \mathcal{V}_{ g , n} }$ for the hyperbolic metric is the current class of |
| + | |||
| + | \begin{equation*} \frac { 1 } { 2 \pi ^ { 2 } } \omega_{ \text{WP}}, \end{equation*} | ||
| + | |||
| + | [[#References|[a14]]]. This result is the basis for a proof of the projectivity of $\overline { \mathcal{M}_ { g , n } }$, [[#References|[a16]]]. | ||
The Weil–Petersson volume element appears in the calculation by E. D'Hoker and D.H. Phong [[#References|[a3]]] of the partition function integrand for the string theory of A.M. Polyakov. Generating functions have also been developed for the volumes of moduli spaces, [[#References|[a4]]], [[#References|[a17]]]. | The Weil–Petersson volume element appears in the calculation by E. D'Hoker and D.H. Phong [[#References|[a3]]] of the partition function integrand for the string theory of A.M. Polyakov. Generating functions have also been developed for the volumes of moduli spaces, [[#References|[a4]]], [[#References|[a17]]]. | ||
| Line 19: | Line 27: | ||
J.F. Brock considers a coarse combinatorial estimate for the Weil–Petersson distance in terms of the edge path metric in the pants complex, [[#References|[a18]]]. | J.F. Brock considers a coarse combinatorial estimate for the Weil–Petersson distance in terms of the edge path metric in the pants complex, [[#References|[a18]]]. | ||
| − | W. Fenchel and J. Nielsen presented "twist-length" coordinates for | + | W. Fenchel and J. Nielsen presented "twist-length" coordinates for $\mathcal{T}_{g,n} $, as the parameters $\{ ( \tau _ { j } , \text{l} _ { j } ) \}$ for assembling pairs of pants, three-holed spheres with hyperbolic metric and geodesic boundaries, to form hyperbolic surfaces. The Kähler form has a simple expression in terms of these coordinates: |
| − | + | \begin{equation*} \omega _ { \text{WP} } = \Sigma _ { j } d \text{l} _ { j } \bigwedge d \tau _ { j }, \end{equation*} | |
| − | [[#References|[a13]]]. Each geodesic length function | + | [[#References|[a13]]]. Each geodesic length function $\mathbf{l}_{*}$ is convex along Weil–Petersson geodesics, [[#References|[a15]]]. Consequently, $\mathcal{T}_{g,n} $ has an exhaustion by compact Weil–Petersson convex sets, [[#References|[a15]]]. |
| − | A. Verjovsky and S. Nag [[#References|[a11]]] considered the Weil–Petersson geometry for the infinite-dimensional universal Teichmüller space and found that the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130060/w13006039.png" /> coincides with the Kirillov–Kostant symplectic structure coming from | + | A. Verjovsky and S. Nag [[#References|[a11]]] considered the Weil–Petersson geometry for the infinite-dimensional universal Teichmüller space and found that the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130060/w13006039.png"/> coincides with the Kirillov–Kostant symplectic structure coming from $\operatorname {Diff}^ { + } ( \mathbf{S} ^ { 1 } ) / \operatorname { Mob } ( \mathbf{S} ^ { 1 } )$. I. Biswas and Nag [[#References|[a2]]] showed that the analogue of the Takhtayan–Zograf result above is valid for the universal moduli space obtained from the inductive limit of Teichmüller spaces for characteristic coverings. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> L.V. Ahlfors, "Some remarks on Teichmüller's space of Riemann surfaces" ''Ann. of Math.'' , '''74''' : 2 (1961) pp. 171–191</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> I. Biswas, S. Nag, "Weil–Petersson geometry and determinant bundles on inductive limits of moduli spaces" , ''Lipa's legacy (New York, 1995)'' , Amer. Math. Soc. (1997) pp. 51–80</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> E. D'Hoker, D.H. Phong, "Multiloop amplitudes for the bosonic Polyakov string" ''Nucl. Phys. B'' , '''269''' : 1 (1986) pp. 205–234</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> R. Kaufmann, Yu. Manin, D. Zagier, "Higher Weil–Petersson volumes of moduli spaces of stable $n$-pointed curves" ''Commun. Math. Phys.'' , '''181''' : 3 (1996) pp. 763–787</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> C.T. McMullen, "The moduli space of Riemann surfaces is Kähler hyperbolic" ''Ann. of Math.'' , '''151''' : 1 (2000) pp. 327–357</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> H. Masur, "Extension of the Weil–Petersson metric to the boundary of Teichmuller space" ''Duke Math. J.'' , '''43''' : 3 (1976) pp. 623–635</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> S. Nag, "The complex analytic theory of Teichmüller spaces" , Wiley/Interscience (1988)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> L.A. Takhtajan, P.G. Zograf, "A local index theorem for families of $\overline { \partial }$-operators on punctured Riemann surfaces and a new Kähler metric on their moduli spaces" ''Commun. Math. Phys.'' , '''137''' : 2 (1991) pp. 399–426</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> A.J. Tromba, "On a natural algebraic affine connection on the space of almost complex structures and the curvature of Teichmüller space with respect to its Weil–Petersson metric" ''Manuscripta Math.'' , '''56''' : 4 (1986) pp. 475–497</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> A.J. Tromba, "Teichmüller theory in Riemannian geometry" , Birkhäuser (1992)</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> S. Nag, A. Verjovsky, "$\operatorname{Diff}( S ^ { 1 } )$ and the Teichmüller spaces" ''Commun. Math. Phys.'' , '''130''' : 1 (1990) pp. 123–138</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> S.A. Wolpert, "Chern forms and the Riemann tensor for the moduli space of curves" ''Invent. Math.'' , '''85''' : 1 (1986) pp. 119–145</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> S.A. Wolpert, "On the Weil–Petersson geometry of the moduli space of curves" ''Amer. J. Math.'' , '''107''' : 4 (1985) pp. 969–997</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> S.A. Wolpert, "The hyperbolic metric and the geometry of the universal curve" ''J. Differential Geom.'' , '''31''' : 2 (1990) pp. 417–472</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> S.A. Wolpert, "Geodesic length functions and the Nielsen problem" ''J. Differential Geom.'' , '''25''' : 2 (1987) pp. 275–296</td></tr><tr><td valign="top">[a16]</td> <td valign="top"> S.A. Wolpert, "On obtaining a positive line bundle from the Weil–Petersson class" ''Amer. J. Math.'' , '''107''' : 6 (1985) pp. 1485–1507</td></tr><tr><td valign="top">[a17]</td> <td valign="top"> P. Zograf, "The Weil–Petersson volume of the moduli space of punctured spheres" , ''Mapping Class Groups and Moduli Spaces of Riemann Surfaces (Göttingen/Seattle, WA, 1991)'' , Amer. Math. Soc. (1993) pp. 367–372</td></tr><tr><td valign="top">[a18]</td> <td valign="top"> J.F. Brock, "The Weil–Petersson metric and volumes of 3-dimensional hyperbolic convex cores" ''Preprint'' (2001)</td></tr></table> |
Revision as of 15:19, 1 July 2020
A. Weil introduced a Kähler metric for the Teichmüller space $T _ { g , n }$, the space of homotopy-marked Riemann surfaces (cf. Riemann surface) of genus $g$ with $n$ punctures and negative Euler characteristic, [a1]. The cotangent space at a marked Riemann surface $\{ R \}$ (the space $Q ( R )$ of holomorphic quadratic differentials on $R$; cf. also Quadratic differential) is considered with the Petersson Hermitian pairing. The Weil–Petersson metric calibrates the variations of the complex structure of $\{ R \}$. The uniformization theorem implies that for a surface of negative Euler characteristic, the following two determinations are equivalent: a complex structure and a complete hyperbolic metric. Accordingly, the Weil–Petersson metric has been studied through quasi-conformal mapping, solution of the inhomogeneous $\overline { \partial }$-equation (cf. also Neumann $\overline { \partial }$-problem), the prescribed curvature equation, and global analysis, [a1], [a7], [a10].
The quotient of the Teichmüller space $\mathcal{T}_{g,n} $ by the action of the mapping class group is the moduli space of Riemann surfaces ${\cal M} _ { g , n }$ (cf. also Moduli of a Riemann surface; Moduli theory); the Weil–Petersson metric is a mapping class group invariant and descends to ${\cal M} _ { g , n }$. $\overline { \mathcal{M}_ { g , n } }$ (the stable-curve compactification of ${\cal M} _ { g , n }$) is a projective variety with $\mathcal{D} _ { g , n } = \overline { \mathcal{M} _ { g , n } } - \mathcal{M} _ { g , n }$ (the divisor of noded stable-curves, i.e. the Riemann surfaces "with disjoint simple loops collapsed to points" and each component of the nodal-complement having negative Euler characteristic). Expansions for the Weil–Petersson metric in a neighbourhood of $\mathcal{D} _ { g , n }$ provide that the metric on ${\cal M} _ { g , n }$ is not complete and that there is a distance completion separating points on $\overline { \mathcal{M}_ { g , n } }$, [a6].
The Weil–Petersson metric has negative sectional curvature, [a9], [a12]. The behaviour near $\mathcal{D} _ { g , n }$ shows that the sectional curvature has as infimum negative infinity and as supremum zero. The holomorphic sectional, Ricci and scalar curvatures are each bounded above by genus-dependent negative constants. A modification of the metric introduced by C.T. McMullen [a5] is Kähler-hyperbolic in the sense of M. Gromov (cf. also Gromov hyperbolic space), has positive first eigenvalue and provides that the sign of the ${\cal M} _ { g , n }$ orbifold Euler characteristic is given by the parity of the dimension.
The Weil–Petersson Kähler form 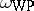 appears in several contexts. L.A. Takhtayan and P.G. Zograf [a8] considered the local index theorem for families of $\overline { \partial }$-operators and calculated the first Chern form of the determinant line bundle $\operatorname{det} \; \operatorname{ind} \overline { \partial }$ using Quillen's construction of a metric based on the hyperbolic metric; the Chern form is
appears in several contexts. L.A. Takhtayan and P.G. Zograf [a8] considered the local index theorem for families of $\overline { \partial }$-operators and calculated the first Chern form of the determinant line bundle $\operatorname{det} \; \operatorname{ind} \overline { \partial }$ using Quillen's construction of a metric based on the hyperbolic metric; the Chern form is
\begin{equation*} \frac { 1 } { 12 \pi ^ { 2 } } \omega _{\text{WP}}. \end{equation*}
The "universal curve" is the fibration $\mathcal{C} _ { g ,\, n }$ over $\mathcal{T}_{g,n} $ with fibre $R$ above the class $\{ R \}$. The uniformization theorem provides a metric for the vertical line bundle ${\cal V} _ { g , n }$ of the fibration. The setup extends to the compactification: The pushdown of the square of the first Chern form of $\overline { \mathcal{V}_{ g , n} }$ for the hyperbolic metric is the current class of
\begin{equation*} \frac { 1 } { 2 \pi ^ { 2 } } \omega_{ \text{WP}}, \end{equation*}
[a14]. This result is the basis for a proof of the projectivity of $\overline { \mathcal{M}_ { g , n } }$, [a16].
The Weil–Petersson volume element appears in the calculation by E. D'Hoker and D.H. Phong [a3] of the partition function integrand for the string theory of A.M. Polyakov. Generating functions have also been developed for the volumes of moduli spaces, [a4], [a17].
J.F. Brock considers a coarse combinatorial estimate for the Weil–Petersson distance in terms of the edge path metric in the pants complex, [a18].
W. Fenchel and J. Nielsen presented "twist-length" coordinates for $\mathcal{T}_{g,n} $, as the parameters $\{ ( \tau _ { j } , \text{l} _ { j } ) \}$ for assembling pairs of pants, three-holed spheres with hyperbolic metric and geodesic boundaries, to form hyperbolic surfaces. The Kähler form has a simple expression in terms of these coordinates:
\begin{equation*} \omega _ { \text{WP} } = \Sigma _ { j } d \text{l} _ { j } \bigwedge d \tau _ { j }, \end{equation*}
[a13]. Each geodesic length function $\mathbf{l}_{*}$ is convex along Weil–Petersson geodesics, [a15]. Consequently, $\mathcal{T}_{g,n} $ has an exhaustion by compact Weil–Petersson convex sets, [a15].
A. Verjovsky and S. Nag [a11] considered the Weil–Petersson geometry for the infinite-dimensional universal Teichmüller space and found that the form 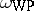 coincides with the Kirillov–Kostant symplectic structure coming from $\operatorname {Diff}^ { + } ( \mathbf{S} ^ { 1 } ) / \operatorname { Mob } ( \mathbf{S} ^ { 1 } )$. I. Biswas and Nag [a2] showed that the analogue of the Takhtayan–Zograf result above is valid for the universal moduli space obtained from the inductive limit of Teichmüller spaces for characteristic coverings.
coincides with the Kirillov–Kostant symplectic structure coming from $\operatorname {Diff}^ { + } ( \mathbf{S} ^ { 1 } ) / \operatorname { Mob } ( \mathbf{S} ^ { 1 } )$. I. Biswas and Nag [a2] showed that the analogue of the Takhtayan–Zograf result above is valid for the universal moduli space obtained from the inductive limit of Teichmüller spaces for characteristic coverings.
References
| [a1] | L.V. Ahlfors, "Some remarks on Teichmüller's space of Riemann surfaces" Ann. of Math. , 74 : 2 (1961) pp. 171–191 |
| [a2] | I. Biswas, S. Nag, "Weil–Petersson geometry and determinant bundles on inductive limits of moduli spaces" , Lipa's legacy (New York, 1995) , Amer. Math. Soc. (1997) pp. 51–80 |
| [a3] | E. D'Hoker, D.H. Phong, "Multiloop amplitudes for the bosonic Polyakov string" Nucl. Phys. B , 269 : 1 (1986) pp. 205–234 |
| [a4] | R. Kaufmann, Yu. Manin, D. Zagier, "Higher Weil–Petersson volumes of moduli spaces of stable $n$-pointed curves" Commun. Math. Phys. , 181 : 3 (1996) pp. 763–787 |
| [a5] | C.T. McMullen, "The moduli space of Riemann surfaces is Kähler hyperbolic" Ann. of Math. , 151 : 1 (2000) pp. 327–357 |
| [a6] | H. Masur, "Extension of the Weil–Petersson metric to the boundary of Teichmuller space" Duke Math. J. , 43 : 3 (1976) pp. 623–635 |
| [a7] | S. Nag, "The complex analytic theory of Teichmüller spaces" , Wiley/Interscience (1988) |
| [a8] | L.A. Takhtajan, P.G. Zograf, "A local index theorem for families of $\overline { \partial }$-operators on punctured Riemann surfaces and a new Kähler metric on their moduli spaces" Commun. Math. Phys. , 137 : 2 (1991) pp. 399–426 |
| [a9] | A.J. Tromba, "On a natural algebraic affine connection on the space of almost complex structures and the curvature of Teichmüller space with respect to its Weil–Petersson metric" Manuscripta Math. , 56 : 4 (1986) pp. 475–497 |
| [a10] | A.J. Tromba, "Teichmüller theory in Riemannian geometry" , Birkhäuser (1992) |
| [a11] | S. Nag, A. Verjovsky, "$\operatorname{Diff}( S ^ { 1 } )$ and the Teichmüller spaces" Commun. Math. Phys. , 130 : 1 (1990) pp. 123–138 |
| [a12] | S.A. Wolpert, "Chern forms and the Riemann tensor for the moduli space of curves" Invent. Math. , 85 : 1 (1986) pp. 119–145 |
| [a13] | S.A. Wolpert, "On the Weil–Petersson geometry of the moduli space of curves" Amer. J. Math. , 107 : 4 (1985) pp. 969–997 |
| [a14] | S.A. Wolpert, "The hyperbolic metric and the geometry of the universal curve" J. Differential Geom. , 31 : 2 (1990) pp. 417–472 |
| [a15] | S.A. Wolpert, "Geodesic length functions and the Nielsen problem" J. Differential Geom. , 25 : 2 (1987) pp. 275–296 |
| [a16] | S.A. Wolpert, "On obtaining a positive line bundle from the Weil–Petersson class" Amer. J. Math. , 107 : 6 (1985) pp. 1485–1507 |
| [a17] | P. Zograf, "The Weil–Petersson volume of the moduli space of punctured spheres" , Mapping Class Groups and Moduli Spaces of Riemann Surfaces (Göttingen/Seattle, WA, 1991) , Amer. Math. Soc. (1993) pp. 367–372 |
| [a18] | J.F. Brock, "The Weil–Petersson metric and volumes of 3-dimensional hyperbolic convex cores" Preprint (2001) |
Weil-Petersson metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil-Petersson_metric&oldid=49870