Difference between revisions of "Small denominators"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48734 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''small divisors'' | ''small divisors'' | ||
Divisors of the form | Divisors of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s0857901.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s0857902.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | which appear in the coefficients of series obtained when integrating differential equations using Taylor series, Fourier series or Poisson series; here | + | which appear in the coefficients of series obtained when integrating differential equations using Taylor series, Fourier series or Poisson series; here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s0857903.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s0857904.png" /> are integer vectors, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s0857905.png" /> is a real vector, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s0857906.png" /> is a complex vector, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s0857907.png" /> denotes the scalar product. The existence of a solution and its properties, such as analyticity, smoothness, etc., depend essentially on the arithmetic nature of the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s0857908.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s0857909.png" /> and the same properties (analyticity, smoothness, etc.) of the differential equations. Conditions are given below which guarantee analyticity of solutions corresponding to analytic problems. These conditions are different for linear and non-linear problems. |
| − | |||
| − | are integer vectors, | ||
| − | is a real vector, | ||
| − | is a complex vector, and | ||
| − | denotes the scalar product. The existence of a solution and its properties, such as analyticity, smoothness, etc., depend essentially on the arithmetic nature of the numbers | ||
| − | |||
| − | and the same properties (analyticity, smoothness, etc.) of the differential equations. Conditions are given below which guarantee analyticity of solutions corresponding to analytic problems. These conditions are different for linear and non-linear problems. | ||
==1. Linear problems.== | ==1. Linear problems.== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | a) Taylor series. The solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579010.png" /> of the equation | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579011.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579012.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579013.png" /> is analytic at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579014.png" /> (where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579015.png" />) and is expressed as the given Taylor series, is given by the Taylor series | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579016.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | This series converges in a neighbourhood of zero if there are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579017.png" /> such that | |
| − | |||
| − | This | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579018.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | + | for all integer-valued <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579020.png" />. This condition is optimal in the class of all analytic functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579021.png" />; it is necessary for the convergence of the series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579022.png" />. | |
| − | |||
| − | + | b) Fourier series. The solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579023.png" /> of the equation | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579024.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579025.png" /> and the right-hand side is expressed as a Fourier series, is given by the Fourier series |
| − | and the right-hand side is expressed as a Fourier series, is given by the Fourier series | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579026.png" /></td> </tr></table> | |
| − | |||
| − | + | which converges in a strip <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579027.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579028.png" /> is analytic and if | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579029.png" /></td> <td valign="top" style="width:5%;text-align:right;">(4)</td></tr></table> | |
| − | |||
| − | + | where the limit is taken over all integer-valued <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579031.png" />. This condition is optimal in the class of all analytic functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579032.png" /> of the form (3). | |
| − | |||
| − | is analytic | ||
| − | + | Equation (3) arises in the reduction of a system of ordinary [[Differential equations on a torus|differential equations on a torus]] (see [[#References|[1]]]; there (2) is erroneously given instead of (4)). The situation is similar when integrating with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579033.png" /> a conditionally-periodic function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579034.png" />. Similar linear problems occur at each approximation in the iterated solution of non-linear problems (in [[Perturbation theory|perturbation theory]]). | |
| − | |||
| − | + | If (2) or (4) are not satisfied, then the non-formal solution of the corresponding problem need not be analytic, smooth or need not exist at all (depending on the arithmetic properties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579035.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579036.png" />), although formal solutions, the series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579038.png" />, always exist (see [[#References|[1]]]). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | If (2) or (4) are not satisfied, then the non-formal solution of the corresponding problem need not be analytic, smooth or need not exist at all (depending on the arithmetic properties of | ||
| − | and | ||
| − | although formal solutions, the series | ||
| − | and | ||
| − | always exist (see [[#References|[1]]]). | ||
==2. Non-linear problems.== | ==2. Non-linear problems.== | ||
In these problems small divisors (1) do not appear singly but in products. | In these problems small divisors (1) do not appear singly but in products. | ||
| − | a) Taylor series. Consider a system near a fixed point | + | a) Taylor series. Consider a system near a fixed point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579039.png" />, |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579040.png" /></td> <td valign="top" style="width:5%;text-align:right;">(5)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579041.png" /> is a convergent Taylor series without free term. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579042.png" /> for integer-valued <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579044.png" />. Then there is a formally invertible change of coordinates | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579045.png" /></td> </tr></table> | |
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579046.png" /> is also a Taylor series without free term, which transforms (5) to the normal form | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579047.png" /></td> <td valign="top" style="width:5%;text-align:right;">(5prm)</td></tr></table> | |
| − | |||
| − | + | The series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579048.png" /> converges in a neighbourhood of zero if | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579049.png" /></td> <td valign="top" style="width:5%;text-align:right;">(6)</td></tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579050.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579051.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579052.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579053.png" /> (see ). |
| − | for | ||
| − | |||
| − | |||
| − | see ). | ||
Non-linear problems of this type were first solved by C.L. Siegel (1942; see , [[#References|[3]]]) under the stricter condition: | Non-linear problems of this type were first solved by C.L. Siegel (1942; see , [[#References|[3]]]) under the stricter condition: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579054.png" /></td> <td valign="top" style="width:5%;text-align:right;">(7)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | Under this condition | + | Under this condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579055.png" /> and (6) converges. Condition (2) is equivalent to boundedness of the terms of (6); it is necessary for the convergence of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579056.png" /> for arbitrary analytic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579057.png" />. (In [[#References|[8]]] necessity of condition (6) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579058.png" /> is claimed; for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579059.png" /> it is unknown what happens in the "gap" between the conditions (2) and (6) (for more complicated resonance situations, see ).) If (2) is not satisfied, then between the solutions of (5) and its normal form (5prm) there need not be an analytic, a smooth or even a topological correspondence. |
| − | and (6) converges. Condition (2) is equivalent to boundedness of the terms of (6); it is necessary for the convergence of | ||
| − | for arbitrary analytic | ||
| − | (In [[#References|[8]]] necessity of condition (6) for | ||
| − | is claimed; for | ||
| − | it is unknown what happens in the "gap" between the conditions (2) and (6) (for more complicated resonance situations, see ).) If (2) is not satisfied, then between the solutions of (5) and its normal form ( | ||
b) Poisson series. Let an analytic system | b) Poisson series. Let an analytic system | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579060.png" /></td> <td valign="top" style="width:5%;text-align:right;">(8)</td></tr></table> | |
| − | |||
| − | the right-hand sides of which are expanded as a Poisson series near the invariant torus | + | the right-hand sides of which are expanded as a Poisson series near the invariant torus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579061.png" /> (that is, a Taylor series with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579062.png" /> and a Fourier series with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579063.png" />), have a formal integral manifold |
| − | that is, a Taylor series with respect to | ||
| − | and a Fourier series with respect to | ||
| − | have a formal integral manifold | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579064.png" /></td> <td valign="top" style="width:5%;text-align:right;">(9)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579065.png" /> is also a Poisson series. The question arises as to when this manifold is analytic (that is, when is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579066.png" /> absolutely convergent for sufficiently small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579067.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579068.png" />). Here, among the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579069.png" /> there may be small parameters; for them <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579070.png" />. Such problems were first solved by A.N. Kolmogorov [[#References|[4]]] for the Hamiltonian system (8) with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579071.png" /> degrees of freedom and one small parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579072.png" /> (that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579073.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579074.png" />): Under the condition |
| − | is also a Poisson series. The question arises as to when this manifold is analytic (that is, when is | ||
| − | absolutely convergent for sufficiently small | ||
| − | and | ||
| − | Here, among the | ||
| − | there may be small parameters; for them | ||
| − | Such problems were first solved by A.N. Kolmogorov [[#References|[4]]] for the Hamiltonian system (8) with | ||
| − | degrees of freedom and one small parameter | ||
| − | that is, | ||
| − | and | ||
| − | Under the condition | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579075.png" /></td> <td valign="top" style="width:5%;text-align:right;">(10)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | the analyticity of the manifold (9), consisting of invariant tori, was proved for | + | the analyticity of the manifold (9), consisting of invariant tori, was proved for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579076.png" />. At the same place it was suggested for the first time that "Newton's method" , which is fundamental in research into non-linear problems, be used for the proof of the convergence of the Poisson series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579077.png" />. Condition (10) and its analogue |
| − | At the same place it was suggested for the first time that "Newton's method" , which is fundamental in research into non-linear problems, be used for the proof of the convergence of the Poisson series | ||
| − | Condition (10) and its analogue | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579078.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
were then used in problems of the same type (see [[#References|[5]]]–[[#References|[7]]]). The conditions (2) and (4) are also necessary here for the convergence of (9) (for more complicated degenerate situations, see [[#References|[7]]]). If these conditions are not satisfied, there need not be an analytic (or even continuous) invariant manifold of the form (9). | were then used in problems of the same type (see [[#References|[5]]]–[[#References|[7]]]). The conditions (2) and (4) are also necessary here for the convergence of (9) (for more complicated degenerate situations, see [[#References|[7]]]). If these conditions are not satisfied, there need not be an analytic (or even continuous) invariant manifold of the form (9). | ||
| − | The most strict of the restrictions (2), (6), (7), condition (7), is, for | + | The most strict of the restrictions (2), (6), (7), condition (7), is, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579079.png" />, satisfied for almost-all (relative to Lebesgue measure) vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579080.png" />. Properties of the type of (2), (6), (7) for vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579081.png" /> are studied in the theory of [[Diophantine approximations|Diophantine approximations]]. The two-dimensional case has been rather well studied. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579082.png" /> be the denominator of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579083.png" />-th convergent of the [[Continued fraction|continued fraction]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579084.png" />. Then (6) is equivalent to convergence of the series |
| − | satisfied for almost-all (relative to Lebesgue measure) vectors | ||
| − | Properties of the type of (2), (6), (7) for vectors | ||
| − | are studied in the theory of [[Diophantine approximations|Diophantine approximations]]. The two-dimensional case has been rather well studied. Let | ||
| − | be the denominator of the | ||
| − | th convergent of the [[Continued fraction|continued fraction]] of | ||
| − | Then (6) is equivalent to convergence of the series | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579085.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
and (2) is equivalent to boundedness of its terms (see also [[#References|[9]]], [[#References|[10]]]). | and (2) is equivalent to boundedness of its terms (see also [[#References|[9]]], [[#References|[10]]]). | ||
| − | Small divisors (1) with variable | + | Small divisors (1) with variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579086.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579087.png" /> have been discussed (see [[#References|[6]]]). |
| − | and | ||
| − | have been discussed (see [[#References|[6]]]). | ||
| − | Small divisors were first encountered in celestial mechanics, and the fundamental linear problems were solved in 1884 by H. Bruns. In general, in the solar system there are many "points of commensurability" between frequencies, a consequence of which are the small divisors (1). For example, the small divisor | + | Small divisors were first encountered in celestial mechanics, and the fundamental linear problems were solved in 1884 by H. Bruns. In general, in the solar system there are many "points of commensurability" between frequencies, a consequence of which are the small divisors (1). For example, the small divisor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579088.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579089.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579090.png" /> are the frequencies of the motions of Jupiter and Saturn, respectively, leads to the appearance of large reciprocal perturbations in the motions of these planets. Another example: the gaps in the asteroid belt and in Saturn's rings correspond to resonance with the frequencies of the perturbing body (Jupiter and Mimas, respectively). |
| − | where | ||
| − | and | ||
| − | are the frequencies of the motions of Jupiter and Saturn, respectively, leads to the appearance of large reciprocal perturbations in the motions of these planets. Another example: the gaps in the asteroid belt and in Saturn's rings correspond to resonance with the frequencies of the perturbing body (Jupiter and Mimas, respectively). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.N. Kolmogorov, "On dynamical systems with integral invariant on a torus" ''Dokl. Akad. Nauk SSSR'' , '''93''' : 5 (1953) pp. 763–766 (In Russian)</TD></TR><TR><TD valign="top">[2a]</TD> <TD valign="top"> A.D. Bryuno, "Analytical form of differential equations" ''Trans. Moscow Math. Soc.'' , '''25''' (1971) pp. 131–288 ''Trudy Moskov. Mat. Obshch.'' , '''25''' (1971) pp. 119–262</TD></TR><TR><TD valign="top">[2b]</TD> <TD valign="top"> A.D. Bryuno, "Analytical form of differential equations" ''Trans. Moscow Math. Soc.'' , '''26''' (1972) pp. 199–239 ''Trudy Moskov. Mat. Obshch.'' , '''26''' (1972) pp. 199–239</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C.L. Siegel, "Vorlesungen über Himmelsmechanik" , Springer (1956)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.N. Kolmogorov, "On conservation of conditionally periodic motions for a small change in the Hamilton functions" ''Dokl. Akad. Nauk SSSR'' , '''98''' : 4 (1954) pp. 527–530 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.K. Moser, "Lectures on Hamiltonian systems" , Amer. Math. Soc. (1968)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.I. Arnol'd, "Small denominators and the problem of stability of motion in classical and celestial mechanics" ''Russian Math. Surveys'' , '''18''' : 6 (1963) pp. 86–191 ''Uspekhi Mat. Nauk'' , '''18''' : 6 (1963) pp. 91–192</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A.D. Bryuno, "Local methods in nonlinear differential equations" , Springer (1989) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> J.Z. Yoccoz, "Linearisation des germs de diffeomorphismes holomorphes de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579091.png" />" ''C.R. Acad. Sci. Paris'' , '''306''' (1988) pp. 55–58</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A.D. [A.D. Bryuno] Bruno, "On small divisors" ''Banach Center Publications'' , '''23''' (1989) pp. 355–359</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> A.D. [A.D. Bryuno] Bruno, "A comparison of conditions on small divisors" ''Preprint IHES'' , '''36''' (1990)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.N. Kolmogorov, "On dynamical systems with integral invariant on a torus" ''Dokl. Akad. Nauk SSSR'' , '''93''' : 5 (1953) pp. 763–766 (In Russian)</TD></TR><TR><TD valign="top">[2a]</TD> <TD valign="top"> A.D. Bryuno, "Analytical form of differential equations" ''Trans. Moscow Math. Soc.'' , '''25''' (1971) pp. 131–288 ''Trudy Moskov. Mat. Obshch.'' , '''25''' (1971) pp. 119–262</TD></TR><TR><TD valign="top">[2b]</TD> <TD valign="top"> A.D. Bryuno, "Analytical form of differential equations" ''Trans. Moscow Math. Soc.'' , '''26''' (1972) pp. 199–239 ''Trudy Moskov. Mat. Obshch.'' , '''26''' (1972) pp. 199–239</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C.L. Siegel, "Vorlesungen über Himmelsmechanik" , Springer (1956)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.N. Kolmogorov, "On conservation of conditionally periodic motions for a small change in the Hamilton functions" ''Dokl. Akad. Nauk SSSR'' , '''98''' : 4 (1954) pp. 527–530 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.K. Moser, "Lectures on Hamiltonian systems" , Amer. Math. Soc. (1968)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.I. Arnol'd, "Small denominators and the problem of stability of motion in classical and celestial mechanics" ''Russian Math. Surveys'' , '''18''' : 6 (1963) pp. 86–191 ''Uspekhi Mat. Nauk'' , '''18''' : 6 (1963) pp. 91–192</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A.D. Bryuno, "Local methods in nonlinear differential equations" , Springer (1989) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> J.Z. Yoccoz, "Linearisation des germs de diffeomorphismes holomorphes de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085790/s08579091.png" />" ''C.R. Acad. Sci. Paris'' , '''306''' (1988) pp. 55–58</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A.D. [A.D. Bryuno] Bruno, "On small divisors" ''Banach Center Publications'' , '''23''' (1989) pp. 355–359</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> A.D. [A.D. Bryuno] Bruno, "A comparison of conditions on small divisors" ''Preprint IHES'' , '''36''' (1990)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| + | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.I. Arnol'd, V. Avez, "Ergodic problems of classical mechanics" , Benjamin (1968) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.I. Arnol'd, V. Avez, "Ergodic problems of classical mechanics" , Benjamin (1968) (Translated from Russian)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
small divisors
Divisors of the form
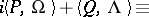 | (1) |
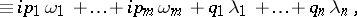 |
which appear in the coefficients of series obtained when integrating differential equations using Taylor series, Fourier series or Poisson series; here 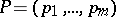 ,
,  are integer vectors,
are integer vectors, 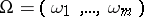 is a real vector,
is a real vector,  is a complex vector, and
is a complex vector, and 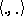 denotes the scalar product. The existence of a solution and its properties, such as analyticity, smoothness, etc., depend essentially on the arithmetic nature of the numbers
denotes the scalar product. The existence of a solution and its properties, such as analyticity, smoothness, etc., depend essentially on the arithmetic nature of the numbers  ,
, 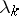 and the same properties (analyticity, smoothness, etc.) of the differential equations. Conditions are given below which guarantee analyticity of solutions corresponding to analytic problems. These conditions are different for linear and non-linear problems.
and the same properties (analyticity, smoothness, etc.) of the differential equations. Conditions are given below which guarantee analyticity of solutions corresponding to analytic problems. These conditions are different for linear and non-linear problems.
1. Linear problems.
a) Taylor series. The solution 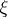 of the equation
of the equation
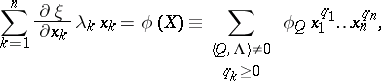 |
where 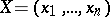 and
and 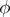 is analytic at
is analytic at 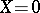 (where
(where 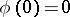 ) and is expressed as the given Taylor series, is given by the Taylor series
) and is expressed as the given Taylor series, is given by the Taylor series
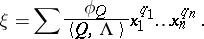 |
This series converges in a neighbourhood of zero if there are 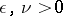 such that
such that
 | (2) |
for all integer-valued 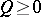 ,
, 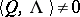 . This condition is optimal in the class of all analytic functions
. This condition is optimal in the class of all analytic functions 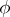 ; it is necessary for the convergence of the series
; it is necessary for the convergence of the series 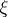 .
.
b) Fourier series. The solution 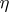 of the equation
of the equation
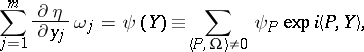 | (3) |
where 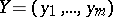 and the right-hand side is expressed as a Fourier series, is given by the Fourier series
and the right-hand side is expressed as a Fourier series, is given by the Fourier series
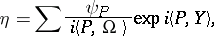 |
which converges in a strip 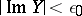 if
if 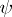 is analytic and if
is analytic and if
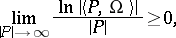 | (4) |
where the limit is taken over all integer-valued 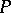 ,
, 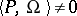 . This condition is optimal in the class of all analytic functions
. This condition is optimal in the class of all analytic functions 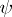 of the form (3).
of the form (3).
Equation (3) arises in the reduction of a system of ordinary differential equations on a torus (see [1]; there (2) is erroneously given instead of (4)). The situation is similar when integrating with respect to 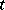 a conditionally-periodic function
a conditionally-periodic function 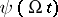 . Similar linear problems occur at each approximation in the iterated solution of non-linear problems (in perturbation theory).
. Similar linear problems occur at each approximation in the iterated solution of non-linear problems (in perturbation theory).
If (2) or (4) are not satisfied, then the non-formal solution of the corresponding problem need not be analytic, smooth or need not exist at all (depending on the arithmetic properties of 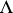 and
and  ), although formal solutions, the series
), although formal solutions, the series 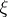 and
and 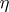 , always exist (see [1]).
, always exist (see [1]).
2. Non-linear problems.
In these problems small divisors (1) do not appear singly but in products.
a) Taylor series. Consider a system near a fixed point 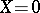 ,
,
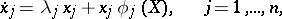 | (5) |
where 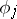 is a convergent Taylor series without free term. Let
is a convergent Taylor series without free term. Let 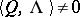 for integer-valued
for integer-valued 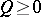 ,
, 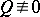 . Then there is a formally invertible change of coordinates
. Then there is a formally invertible change of coordinates
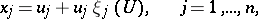 |
where 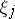 is also a Taylor series without free term, which transforms (5) to the normal form
is also a Taylor series without free term, which transforms (5) to the normal form
 | (5prm) |
The series 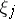 converges in a neighbourhood of zero if
converges in a neighbourhood of zero if
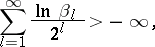 | (6) |
where 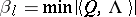 for
for 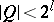 ,
, 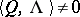 ,
, 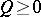 (see ).
(see ).
Non-linear problems of this type were first solved by C.L. Siegel (1942; see , [3]) under the stricter condition:
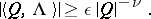 | (7) |
Under this condition 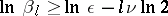 and (6) converges. Condition (2) is equivalent to boundedness of the terms of (6); it is necessary for the convergence of
and (6) converges. Condition (2) is equivalent to boundedness of the terms of (6); it is necessary for the convergence of 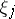 for arbitrary analytic
for arbitrary analytic 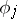 . (In [8] necessity of condition (6) for
. (In [8] necessity of condition (6) for 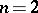 is claimed; for
is claimed; for 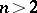 it is unknown what happens in the "gap" between the conditions (2) and (6) (for more complicated resonance situations, see ).) If (2) is not satisfied, then between the solutions of (5) and its normal form (5prm) there need not be an analytic, a smooth or even a topological correspondence.
it is unknown what happens in the "gap" between the conditions (2) and (6) (for more complicated resonance situations, see ).) If (2) is not satisfied, then between the solutions of (5) and its normal form (5prm) there need not be an analytic, a smooth or even a topological correspondence.
b) Poisson series. Let an analytic system
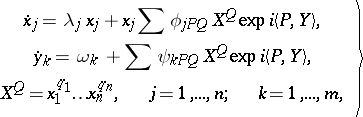 | (8) |
the right-hand sides of which are expanded as a Poisson series near the invariant torus 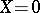 (that is, a Taylor series with respect to
(that is, a Taylor series with respect to 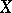 and a Fourier series with respect to
and a Fourier series with respect to 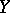 ), have a formal integral manifold
), have a formal integral manifold
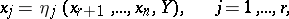 | (9) |
where 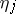 is also a Poisson series. The question arises as to when this manifold is analytic (that is, when is
is also a Poisson series. The question arises as to when this manifold is analytic (that is, when is 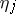 absolutely convergent for sufficiently small
absolutely convergent for sufficiently small 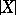 and
and 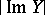 ). Here, among the
). Here, among the 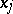 there may be small parameters; for them
there may be small parameters; for them 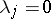 . Such problems were first solved by A.N. Kolmogorov [4] for the Hamiltonian system (8) with
. Such problems were first solved by A.N. Kolmogorov [4] for the Hamiltonian system (8) with 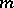 degrees of freedom and one small parameter
degrees of freedom and one small parameter 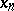 (that is,
(that is, 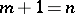 and
and 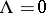 ): Under the condition
): Under the condition
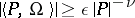 | (10) |
the analyticity of the manifold (9), consisting of invariant tori, was proved for 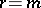 . At the same place it was suggested for the first time that "Newton's method" , which is fundamental in research into non-linear problems, be used for the proof of the convergence of the Poisson series
. At the same place it was suggested for the first time that "Newton's method" , which is fundamental in research into non-linear problems, be used for the proof of the convergence of the Poisson series 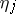 . Condition (10) and its analogue
. Condition (10) and its analogue
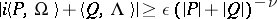 |
were then used in problems of the same type (see [5]–[7]). The conditions (2) and (4) are also necessary here for the convergence of (9) (for more complicated degenerate situations, see [7]). If these conditions are not satisfied, there need not be an analytic (or even continuous) invariant manifold of the form (9).
The most strict of the restrictions (2), (6), (7), condition (7), is, for 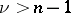 , satisfied for almost-all (relative to Lebesgue measure) vectors
, satisfied for almost-all (relative to Lebesgue measure) vectors 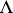 . Properties of the type of (2), (6), (7) for vectors
. Properties of the type of (2), (6), (7) for vectors 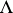 are studied in the theory of Diophantine approximations. The two-dimensional case has been rather well studied. Let
are studied in the theory of Diophantine approximations. The two-dimensional case has been rather well studied. Let 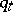 be the denominator of the
be the denominator of the 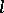 -th convergent of the continued fraction of
-th convergent of the continued fraction of 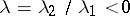 . Then (6) is equivalent to convergence of the series
. Then (6) is equivalent to convergence of the series
 |
and (2) is equivalent to boundedness of its terms (see also [9], [10]).
Small divisors (1) with variable  and
and 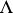 have been discussed (see [6]).
have been discussed (see [6]).
Small divisors were first encountered in celestial mechanics, and the fundamental linear problems were solved in 1884 by H. Bruns. In general, in the solar system there are many "points of commensurability" between frequencies, a consequence of which are the small divisors (1). For example, the small divisor 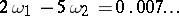 , where
, where 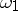 and
and 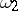 are the frequencies of the motions of Jupiter and Saturn, respectively, leads to the appearance of large reciprocal perturbations in the motions of these planets. Another example: the gaps in the asteroid belt and in Saturn's rings correspond to resonance with the frequencies of the perturbing body (Jupiter and Mimas, respectively).
are the frequencies of the motions of Jupiter and Saturn, respectively, leads to the appearance of large reciprocal perturbations in the motions of these planets. Another example: the gaps in the asteroid belt and in Saturn's rings correspond to resonance with the frequencies of the perturbing body (Jupiter and Mimas, respectively).
References
| [1] | A.N. Kolmogorov, "On dynamical systems with integral invariant on a torus" Dokl. Akad. Nauk SSSR , 93 : 5 (1953) pp. 763–766 (In Russian) |
| [2a] | A.D. Bryuno, "Analytical form of differential equations" Trans. Moscow Math. Soc. , 25 (1971) pp. 131–288 Trudy Moskov. Mat. Obshch. , 25 (1971) pp. 119–262 |
| [2b] | A.D. Bryuno, "Analytical form of differential equations" Trans. Moscow Math. Soc. , 26 (1972) pp. 199–239 Trudy Moskov. Mat. Obshch. , 26 (1972) pp. 199–239 |
| [3] | C.L. Siegel, "Vorlesungen über Himmelsmechanik" , Springer (1956) |
| [4] | A.N. Kolmogorov, "On conservation of conditionally periodic motions for a small change in the Hamilton functions" Dokl. Akad. Nauk SSSR , 98 : 4 (1954) pp. 527–530 (In Russian) |
| [5] | J.K. Moser, "Lectures on Hamiltonian systems" , Amer. Math. Soc. (1968) |
| [6] | V.I. Arnol'd, "Small denominators and the problem of stability of motion in classical and celestial mechanics" Russian Math. Surveys , 18 : 6 (1963) pp. 86–191 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 91–192 |
| [7] | A.D. Bryuno, "Local methods in nonlinear differential equations" , Springer (1989) (Translated from Russian) |
| [8] | J.Z. Yoccoz, "Linearisation des germs de diffeomorphismes holomorphes de 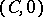 " C.R. Acad. Sci. Paris , 306 (1988) pp. 55–58 " C.R. Acad. Sci. Paris , 306 (1988) pp. 55–58 |
| [9] | A.D. [A.D. Bryuno] Bruno, "On small divisors" Banach Center Publications , 23 (1989) pp. 355–359 |
| [10] | A.D. [A.D. Bryuno] Bruno, "A comparison of conditions on small divisors" Preprint IHES , 36 (1990) |
Comments
References
| [a1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
| [a2] | V.I. Arnol'd, V. Avez, "Ergodic problems of classical mechanics" , Benjamin (1968) (Translated from Russian) |
Small denominators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Small_denominators&oldid=49430