Difference between revisions of "Schottky problem"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48620 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | To a complete non-singular [[Algebraic curve|algebraic curve]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s0833801.png" /> of genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s0833802.png" /> one can associate its Jacobian (cf. [[Jacobi variety|Jacobi variety]]). This is an [[Abelian variety|Abelian variety]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s0833803.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s0833804.png" /> together with a principal polarization <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s0833805.png" /> (cf. [[Polarized algebraic variety|Polarized algebraic variety]]). B. Riemann showed in 1857 that algebraic curves of genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s0833806.png" /> depend on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s0833807.png" /> parameters (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s0833808.png" />). But principally-polarized Abelian varieties of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s0833809.png" /> depend on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338010.png" /> parameters. Since for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338011.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338012.png" />, the question arises which principally-polarized Abelian varieties are Jacobians. This question was posed by Riemann, but is known as the Schottky problem. More precisely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338013.png" /> is the moduli space of curves of genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338014.png" /> (i.e. the parameter space of isomorphism classes of such curves of genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338015.png" />, cf. [[Moduli theory|Moduli theory]]) and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338016.png" /> is the moduli space of principally-polarized Abelian varieties of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338017.png" />, there is a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338018.png" />, and the problem is to characterize the closure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338019.png" /> of its image. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338020.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338021.png" />. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Here only the case where the curve is a complex curve or Riemann surface is considered. If one chooses a symplectic basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338023.png" /> of the homology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338024.png" /> and a basis of the space of holomorphic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338025.png" />-forms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338026.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338027.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338028.png" /> (Kronecker delta), one obtains the period matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338029.png" />. This matrix lies in the Siegel upper half-space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338030.png" />, the set of all complex symmetric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338031.png" />-matrices whose imaginary part is positive definite. | |
| − | |||
| − | + | The Jacobian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338032.png" /> is given by the complex torus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338033.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338034.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338035.png" /> is then the divisor of Riemann's [[Theta-function|theta-function]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | is the | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338036.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The | + | The moduli space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338037.png" /> can be obtained as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338038.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338039.png" /> acts naturally on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338040.png" />. Coordinates on (a covering of) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338041.png" /> are provided by the "theta constanttheta constants" , which are the values at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338042.png" /> of the theta-functions |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338043.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338044.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The first result is due to W. Schottky for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338045.png" />. He showed in 1888 that a certain polynomial of degree 16 in the theta constants vanished on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338046.png" />, but not everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338047.png" />. J.-I. Igusa showed much later that its [[Zero divisor|zero divisor]] equals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338048.png" />. | |
| − | |||
| − | + | The next step was made by Schottky and H.W.E. Jung in 1909, who constructed expressions in the theta constants that vanish on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338049.png" /> by means of double unramified coverings of curves. (Today this is called the theory of Prym varieties.) These expressions define a certain locus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338050.png" /> (called the Schottky locus) which contains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338051.png" />. It is conjectured that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338052.png" />, and this is the Schottky problem in restricted sense. B. van Geemen showed in 1983 that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338053.png" /> is an irreducible component of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338054.png" />. | |
| − | + | Since the Schottky problem asks for a characterization, different approaches might lead to different answers. One approach uses the fact that the theta divisor of a Jacobian is singular (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338055.png" />): the dimension of its singular locus is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338056.png" />. It is therefore natural to consider the locus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338057.png" /> of principally-polarized Abelian varieties <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338058.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338059.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338060.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338061.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338062.png" /> is indeed an irreducible component, as A. Andreotti and A. Mayer showed. However, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338063.png" /> has other components, so this is not strong enough. | |
| − | |||
| − | |||
| − | |||
| − | + | Another way to try to distinguish Jacobians and general principally-polarized Abelian varieties uses trisecants. Below, only principally-polarized Abelian varieties that are indecomposable, i.e. not products, are considered. For such an Abelian variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338064.png" /> there is a mapping to projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338065.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338066.png" /> given by the theta-functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338067.png" /> and its image is the Kummer variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338068.png" /> (cf. [[Kummer surface|Kummer surface]]). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338069.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338070.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338071.png" /> is such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338072.png" />, then the three points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338073.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338074.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338075.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338076.png" /> are collinear, i.e. define a trisecant. (Translated in terms of theta-functions this is Fay's trisecant identity.) It is conjectured that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338077.png" /> is an indecomposable principally-polarized Abelian variety whose Kummer variety admits a trisecant, then it is a Jacobian. (It was proved by A. Beauville and O. Debarre that the existence of a trisecant implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338078.png" />.) A weakened version of this is proved by R.C. Gunning and G. Welters. A simplified form reads: If the Kummer variety admits a continuous family of trisecants and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338079.png" />, then the Abelian variety is a Jacobian. | |
| − | |||
| − | |||
| − | It is conjectured that | ||
| − | and this is the | ||
| − | is | ||
| − | + | One can consider an infinitesimal version of this. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338080.png" />. Then the criterion is: The Abelian variety is a Jacobian if there exist constant vector fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338081.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338082.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338083.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338084.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338085.png" /> such that | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338086.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
This is known as Novikov's conjecture and was proved by M. Shiota in 1986. Another (more geometric) proof was given by E. Arbarello and C. De Concini. The equation (*) is called the K–P-equation (after Kadomtsev–Petviashvili) and generalizes the [[Korteweg–de Vries equation|Korteweg–de Vries equation]]. It is the first of a whole hierarchy of equations. | This is known as Novikov's conjecture and was proved by M. Shiota in 1986. Another (more geometric) proof was given by E. Arbarello and C. De Concini. The equation (*) is called the K–P-equation (after Kadomtsev–Petviashvili) and generalizes the [[Korteweg–de Vries equation|Korteweg–de Vries equation]]. It is the first of a whole hierarchy of equations. | ||
| Line 138: | Line 29: | ||
By the Riemann identity | By the Riemann identity | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338087.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | this translates into the fact that | + | this translates into the fact that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338088.png" /> satisfies the partial differential equation |
| − | satisfies the partial differential equation | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338089.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | Yet another approach (due to van Geemen and G. van der Geer) and gives a connection to the approach using the K–P-equation. The theta-functions | + | Yet another approach (due to van Geemen and G. van der Geer) and gives a connection to the approach using the K–P-equation. The theta-functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338090.png" /> map an Abelian variety to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338091.png" />. They also define a mapping from the moduli space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338092.png" /> (a covering of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338093.png" />) to this projective space, where the image of the class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338094.png" /> is the image of the origin of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338095.png" /> under <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338096.png" />. It is conjectured that the intersection of the image of the moduli space and the Kummer variety of an indecomposable Abelian variety has dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338097.png" /> and equals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338098.png" /> exactly when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s08338099.png" /> is a Jacobian. Similarly for the intersection of the Kummer variety and the tangent space to the moduli space at the point defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380100.png" />. By the heat equation for the theta-function this last conjecture is equivalent to a statement about the set of common zeros <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380101.png" /> of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380102.png" /> of theta-functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380103.png" /> (for fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380104.png" />) which vanish with multiplicity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380105.png" /> at the origin of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380106.png" />. For a Jacobian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380107.png" /> this set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380108.png" /> consists of the image <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380109.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380110.png" /> in the Jacobian (with a slight exception for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380111.png" />), as was proved by Welters. Conjecturally, Jacobians are now characterized by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380112.png" />. |
| − | map an Abelian variety to | ||
| − | They also define a mapping from the moduli space | ||
| − | a covering of | ||
| − | to this projective space, where the image of the class of | ||
| − | is the image of the origin of | ||
| − | under | ||
| − | It is conjectured that the intersection of the image of the moduli space and the Kummer variety of an indecomposable Abelian variety has dimension | ||
| − | and equals | ||
| − | exactly when | ||
| − | is a Jacobian. Similarly for the intersection of the Kummer variety and the tangent space to the moduli space at the point defined by | ||
| − | By the heat equation for the theta-function this last conjecture is equivalent to a statement about the set of common zeros | ||
| − | of the space | ||
| − | of theta-functions | ||
| − | for fixed | ||
| − | which vanish with multiplicity | ||
| − | at the origin of | ||
| − | For a Jacobian | ||
| − | this set | ||
| − | consists of the image | ||
| − | of | ||
| − | in the Jacobian (with a slight exception for | ||
| − | as was proved by Welters. Conjecturally, Jacobians are now characterized by | ||
| − | These conjectures were refined by R. Donagi in [[#References|[a2]]] to a much stronger conjecture which describes the Schottky locus | + | These conjectures were refined by R. Donagi in [[#References|[a2]]] to a much stronger conjecture which describes the Schottky locus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380113.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380114.png" />, the moduli space of principally-polarized Abelian varieties <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380115.png" /> with a non-zero point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380116.png" /> of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380117.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380118.png" />. This conjecture is very strong: it implies a strengthened version of the Novikov conjecture and all the conjectures of van Geemen and van der Geer. These last ones are obtained by intersecting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380119.png" /> with the boundary of the compactified moduli space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380120.png" />, while the Novikov conjecture follows by infinitesimalizing this. Donagi proved his conjecture for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083380/s083380121.png" />. |
| − | in | ||
| − | the moduli space of principally-polarized Abelian varieties | ||
| − | with a non-zero point | ||
| − | of order | ||
| − | on | ||
| − | This conjecture is very strong: it implies a strengthened version of the Novikov conjecture and all the conjectures of van Geemen and van der Geer. These last ones are obtained by intersecting | ||
| − | with the boundary of the compactified moduli space | ||
| − | while the Novikov conjecture follows by infinitesimalizing this. Donagi proved his conjecture for | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Beauville, "Le problème de Schottky et la conjecture de Novikov" ''Astérisque'' , '''152–153''' (1988) pp. 101–112 (Sém Bourbaki, Exp. 675)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Donagi, "The Schottky problem" E. Sernesi (ed.) , ''Theory of Moduli'' , ''Lect. notes in math.'' , '''1337''' , Springer (1988) pp. 84–137</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G. van der Geer, "The Schottky problem" F. Hirzebruch (ed.) J. Schwermer (ed.) S. Suter (ed.) , ''Arbeitstagung Bonn 1984'' , ''Lect. notes in math.'' , '''1111''' , Springer (1985) pp. 385–406</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D. Mumford, "Curves and their Jacobians" , Univ. Michigan Press (1975)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Beauville, "Le problème de Schottky et la conjecture de Novikov" ''Astérisque'' , '''152–153''' (1988) pp. 101–112 (Sém Bourbaki, Exp. 675)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Donagi, "The Schottky problem" E. Sernesi (ed.) , ''Theory of Moduli'' , ''Lect. notes in math.'' , '''1337''' , Springer (1988) pp. 84–137</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G. van der Geer, "The Schottky problem" F. Hirzebruch (ed.) J. Schwermer (ed.) S. Suter (ed.) , ''Arbeitstagung Bonn 1984'' , ''Lect. notes in math.'' , '''1111''' , Springer (1985) pp. 385–406</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D. Mumford, "Curves and their Jacobians" , Univ. Michigan Press (1975)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
To a complete non-singular algebraic curve 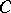 of genus
of genus 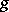 one can associate its Jacobian (cf. Jacobi variety). This is an Abelian variety
one can associate its Jacobian (cf. Jacobi variety). This is an Abelian variety 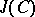 of dimension
of dimension 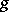 together with a principal polarization
together with a principal polarization 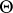 (cf. Polarized algebraic variety). B. Riemann showed in 1857 that algebraic curves of genus
(cf. Polarized algebraic variety). B. Riemann showed in 1857 that algebraic curves of genus 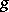 depend on
depend on 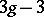 parameters (for
parameters (for 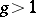 ). But principally-polarized Abelian varieties of dimension
). But principally-polarized Abelian varieties of dimension 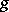 depend on
depend on 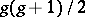 parameters. Since for
parameters. Since for 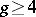 one has
one has 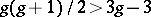 , the question arises which principally-polarized Abelian varieties are Jacobians. This question was posed by Riemann, but is known as the Schottky problem. More precisely, if
, the question arises which principally-polarized Abelian varieties are Jacobians. This question was posed by Riemann, but is known as the Schottky problem. More precisely, if 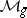 is the moduli space of curves of genus
is the moduli space of curves of genus 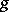 (i.e. the parameter space of isomorphism classes of such curves of genus
(i.e. the parameter space of isomorphism classes of such curves of genus 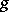 , cf. Moduli theory) and if
, cf. Moduli theory) and if 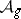 is the moduli space of principally-polarized Abelian varieties of dimension
is the moduli space of principally-polarized Abelian varieties of dimension 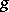 , there is a mapping
, there is a mapping 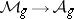 , and the problem is to characterize the closure
, and the problem is to characterize the closure 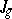 of its image. For
of its image. For 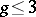 one has
one has 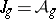 .
.
Here only the case where the curve is a complex curve or Riemann surface is considered. If one chooses a symplectic basis 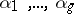 ,
, 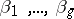 of the homology
of the homology 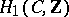 and a basis of the space of holomorphic
and a basis of the space of holomorphic 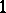 -forms
-forms 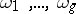 on
on 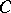 such that
such that 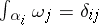 (Kronecker delta), one obtains the period matrix
(Kronecker delta), one obtains the period matrix 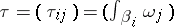 . This matrix lies in the Siegel upper half-space
. This matrix lies in the Siegel upper half-space 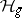 , the set of all complex symmetric
, the set of all complex symmetric  -matrices whose imaginary part is positive definite.
-matrices whose imaginary part is positive definite.
The Jacobian 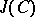 is given by the complex torus
is given by the complex torus 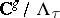 , where
, where 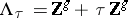 , and
, and 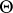 is then the divisor of Riemann's theta-function
is then the divisor of Riemann's theta-function
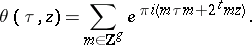 |
The moduli space 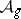 can be obtained as
can be obtained as 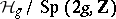 , where
, where 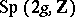 acts naturally on
acts naturally on 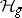 . Coordinates on (a covering of)
. Coordinates on (a covering of) 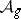 are provided by the "theta constanttheta constants" , which are the values at
are provided by the "theta constanttheta constants" , which are the values at 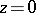 of the theta-functions
of the theta-functions
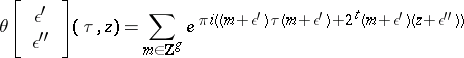 |
for 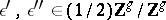 .
.
The first result is due to W. Schottky for 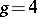 . He showed in 1888 that a certain polynomial of degree 16 in the theta constants vanished on
. He showed in 1888 that a certain polynomial of degree 16 in the theta constants vanished on 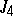 , but not everywhere on
, but not everywhere on 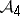 . J.-I. Igusa showed much later that its zero divisor equals
. J.-I. Igusa showed much later that its zero divisor equals 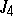 .
.
The next step was made by Schottky and H.W.E. Jung in 1909, who constructed expressions in the theta constants that vanish on 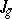 by means of double unramified coverings of curves. (Today this is called the theory of Prym varieties.) These expressions define a certain locus
by means of double unramified coverings of curves. (Today this is called the theory of Prym varieties.) These expressions define a certain locus 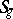 (called the Schottky locus) which contains
(called the Schottky locus) which contains  . It is conjectured that
. It is conjectured that 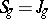 , and this is the Schottky problem in restricted sense. B. van Geemen showed in 1983 that
, and this is the Schottky problem in restricted sense. B. van Geemen showed in 1983 that 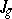 is an irreducible component of
is an irreducible component of 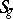 .
.
Since the Schottky problem asks for a characterization, different approaches might lead to different answers. One approach uses the fact that the theta divisor of a Jacobian is singular (for 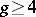 ): the dimension of its singular locus is
): the dimension of its singular locus is 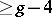 . It is therefore natural to consider the locus
. It is therefore natural to consider the locus 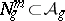 of principally-polarized Abelian varieties
of principally-polarized Abelian varieties 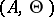 of dimension
of dimension  with
with 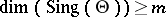 . Then
. Then 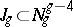 , and
, and 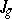 is indeed an irreducible component, as A. Andreotti and A. Mayer showed. However,
is indeed an irreducible component, as A. Andreotti and A. Mayer showed. However, 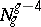 has other components, so this is not strong enough.
has other components, so this is not strong enough.
Another way to try to distinguish Jacobians and general principally-polarized Abelian varieties uses trisecants. Below, only principally-polarized Abelian varieties that are indecomposable, i.e. not products, are considered. For such an Abelian variety 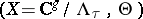 there is a mapping to projective space
there is a mapping to projective space 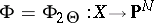 with
with 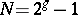 given by the theta-functions
given by the theta-functions 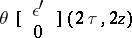 and its image is the Kummer variety
and its image is the Kummer variety 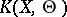 (cf. Kummer surface). If
(cf. Kummer surface). If 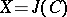 and
and 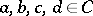 and if
and if 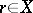 is such that
is such that 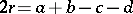 , then the three points
, then the three points 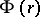 ,
,  and
and 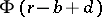 in
in 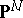 are collinear, i.e. define a trisecant. (Translated in terms of theta-functions this is Fay's trisecant identity.) It is conjectured that if
are collinear, i.e. define a trisecant. (Translated in terms of theta-functions this is Fay's trisecant identity.) It is conjectured that if 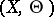 is an indecomposable principally-polarized Abelian variety whose Kummer variety admits a trisecant, then it is a Jacobian. (It was proved by A. Beauville and O. Debarre that the existence of a trisecant implies
is an indecomposable principally-polarized Abelian variety whose Kummer variety admits a trisecant, then it is a Jacobian. (It was proved by A. Beauville and O. Debarre that the existence of a trisecant implies 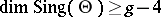 .) A weakened version of this is proved by R.C. Gunning and G. Welters. A simplified form reads: If the Kummer variety admits a continuous family of trisecants and
.) A weakened version of this is proved by R.C. Gunning and G. Welters. A simplified form reads: If the Kummer variety admits a continuous family of trisecants and 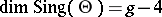 , then the Abelian variety is a Jacobian.
, then the Abelian variety is a Jacobian.
One can consider an infinitesimal version of this. Let 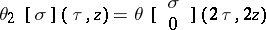 . Then the criterion is: The Abelian variety is a Jacobian if there exist constant vector fields
. Then the criterion is: The Abelian variety is a Jacobian if there exist constant vector fields 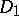 ,
, 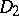 ,
, 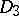 on
on 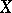 and
and 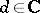 such that
such that
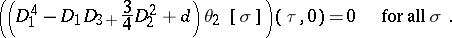 | (*) |
This is known as Novikov's conjecture and was proved by M. Shiota in 1986. Another (more geometric) proof was given by E. Arbarello and C. De Concini. The equation (*) is called the K–P-equation (after Kadomtsev–Petviashvili) and generalizes the Korteweg–de Vries equation. It is the first of a whole hierarchy of equations.
By the Riemann identity
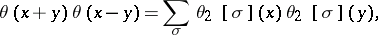 |
this translates into the fact that 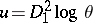 satisfies the partial differential equation
satisfies the partial differential equation
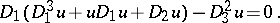 |
Yet another approach (due to van Geemen and G. van der Geer) and gives a connection to the approach using the K–P-equation. The theta-functions 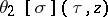 map an Abelian variety to
map an Abelian variety to 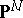 . They also define a mapping from the moduli space
. They also define a mapping from the moduli space 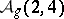 (a covering of
(a covering of 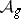 ) to this projective space, where the image of the class of
) to this projective space, where the image of the class of 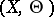 is the image of the origin of
is the image of the origin of 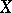 under
under 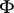 . It is conjectured that the intersection of the image of the moduli space and the Kummer variety of an indecomposable Abelian variety has dimension
. It is conjectured that the intersection of the image of the moduli space and the Kummer variety of an indecomposable Abelian variety has dimension 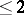 and equals
and equals  exactly when
exactly when 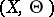 is a Jacobian. Similarly for the intersection of the Kummer variety and the tangent space to the moduli space at the point defined by
is a Jacobian. Similarly for the intersection of the Kummer variety and the tangent space to the moduli space at the point defined by 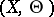 . By the heat equation for the theta-function this last conjecture is equivalent to a statement about the set of common zeros
. By the heat equation for the theta-function this last conjecture is equivalent to a statement about the set of common zeros 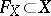 of the space
of the space 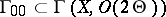 of theta-functions
of theta-functions 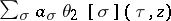 (for fixed
(for fixed  ) which vanish with multiplicity
) which vanish with multiplicity 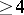 at the origin of
at the origin of 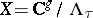 . For a Jacobian
. For a Jacobian 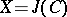 this set
this set 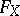 consists of the image
consists of the image 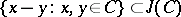 of
of 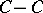 in the Jacobian (with a slight exception for
in the Jacobian (with a slight exception for 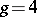 ), as was proved by Welters. Conjecturally, Jacobians are now characterized by
), as was proved by Welters. Conjecturally, Jacobians are now characterized by 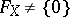 .
.
These conjectures were refined by R. Donagi in [a2] to a much stronger conjecture which describes the Schottky locus 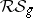 in
in 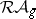 , the moduli space of principally-polarized Abelian varieties
, the moduli space of principally-polarized Abelian varieties 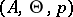 with a non-zero point
with a non-zero point 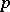 of order
of order  on
on 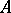 . This conjecture is very strong: it implies a strengthened version of the Novikov conjecture and all the conjectures of van Geemen and van der Geer. These last ones are obtained by intersecting
. This conjecture is very strong: it implies a strengthened version of the Novikov conjecture and all the conjectures of van Geemen and van der Geer. These last ones are obtained by intersecting 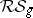 with the boundary of the compactified moduli space
with the boundary of the compactified moduli space 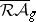 , while the Novikov conjecture follows by infinitesimalizing this. Donagi proved his conjecture for
, while the Novikov conjecture follows by infinitesimalizing this. Donagi proved his conjecture for 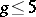 .
.
References
| [a1] | A. Beauville, "Le problème de Schottky et la conjecture de Novikov" Astérisque , 152–153 (1988) pp. 101–112 (Sém Bourbaki, Exp. 675) |
| [a2] | R. Donagi, "The Schottky problem" E. Sernesi (ed.) , Theory of Moduli , Lect. notes in math. , 1337 , Springer (1988) pp. 84–137 |
| [a3] | G. van der Geer, "The Schottky problem" F. Hirzebruch (ed.) J. Schwermer (ed.) S. Suter (ed.) , Arbeitstagung Bonn 1984 , Lect. notes in math. , 1111 , Springer (1985) pp. 385–406 |
| [a4] | D. Mumford, "Curves and their Jacobians" , Univ. Michigan Press (1975) |
Schottky problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schottky_problem&oldid=49416