Namespaces
Variants
Actions

Difference between revisions of "Rotation theorems"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48592 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
Theorems which characterize the change in the argument under a [[Conformal mapping|conformal mapping]]. Rotation theorems in the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r0826801.png" /> of functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r0826802.png" /> which are regular and univalent in the disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r0826803.png" /> give accurate estimates of the argument of the derivative for functions of this class:
−
r0826801.png
 
−
$#A+1 = 18 n = 0
 
−
$#C+1 = 18 : ~/encyclopedia/old_files/data/R082/R.0802680 Rotation theorems
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r0826804.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table>
−
{{TEX|done}}
 
  
−
Theorems which characterize the change in the argument under a [[Conformal mapping|conformal mapping]]. Rotation theorems in the class  $  S $
+
Here one considers the branch of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r0826805.png" /> that vanishes when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r0826806.png" />. The upper and the lower bounds for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r0826807.png" /> given by the inequalities (*) are sharp for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r0826808.png" /> in the disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r0826809.png" />. This rotation theorem was obtained by G.M. Goluzin [[#References|[1]]], [[#References|[5]]]; I.E. Bazilevich [[#References|[2]]] was the first to show that the inequalities (*) are sharp for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r08268010.png" />; J.A. Jenkins [[#References|[3]]] gave a complete analysis of the cases of equality in these estimates.
−
of functions  $  f( z) = z + c _ {2} z  ^ {2} + \dots $
 
−
which are regular and univalent in the disc  $  | z | < 1 $
 
−
give accurate estimates of the argument of the derivative for functions of this class:
 
  
−
$$ \tag{* }
+
Rotation theorems in the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r08268012.png" /> is also the name given to estimates of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r08268013.png" /> and to estimates of expressions of the type
−
|  \mathop{\rm arg}  f ^ { \prime } ( z) |  \leq  \left \{
 
  
−
Here one considers the branch of  $  \mathop{\rm arg}  f ^ { \prime } ( z) $
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r08268014.png" /></td> </tr></table>
−
that vanishes when  $  z = 0 $.  
 
−
The upper and the lower bounds for  $  \mathop{\rm arg}  f ^ { \prime } ( z) $
 
−
given by the inequalities (*) are sharp for any  $  z $
 
−
in the disc  $  | z | < 1 $.  
 
−
This rotation theorem was obtained by G.M. Goluzin [[#References|[1]]], [[#References|[5]]]; I.E. Bazilevich [[#References|[2]]] was the first to show that the inequalities (*) are sharp for  $  2 ^ {- 1/2 } < | z | < 1 $;
 
−
J.A. Jenkins [[#References|[3]]] gave a complete analysis of the cases of equality in these estimates.
 
  
−
Rotation theorems in the class $  S $
+
The simplest estimates of this type in the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r08268015.png" /> are the sharp inequalities (the appropriate branches of the arguments are considered):
−
is also the name given to estimates of  $  \mathop{\rm arg} ( f( z)/z) $
 
−
and to estimates of expressions of the type
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r08268016.png" /></td> </tr></table>
−
\lambda  \mathop{\rm arg}  f ^ { \prime } ( z) - ( 1 - \lambda )  \mathop{\rm arg} \
 
  
−
\frac{f ( z) }{z }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r08268017.png" /></td> </tr></table>
−
,\ \
 
−
0 < \lambda < 1.
 
−
$$
 
  
−
The simplest estimates of this type in the class  $  S $
+
There are also rotation theorems in other classes of functions which realize a univalent conformal mapping of the disc or its exterior, and in classes of functions which are univalent in a multiply-connected domain (cf. [[#References|[5]]], [[#References|[3]]], [[Distortion theorems|Distortion theorems]]; [[Univalent function|Univalent function]]). Rotation theorems have also been extended to include the case of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r08268018.png" />-valued functions (cf. addenda to [[#References|[5]]], and also [[Multivalent function|Multivalent function]]).
−
are the sharp inequalities (the appropriate branches of the arguments are considered):
 
  
−
$$
+
====References====
−
\left | \mathop{\rm arg}  
+
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.M. Goluzin,  "On distortion theorems in the theory of conformal mappings" ''Mat. Sb.'' , '''1 (43)''' :  1 (1936) pp. 127–135 (In Russian) (German abstract)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.E. Bazilevich,  "Sur les théorèmes de Koebe–Bieberbach" ''Mat. Sb.'' , '''1 (43)''' :  3  (1936)  pp. 283–292</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  J.A. Jenkins,  "Univalent functions and conformal mapping" , Springer (1958)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Grunsky,  "Neue Abschätzungen zur konformen Abbildung ein- und mehrfach zusammenhängender Bereiche" ''Schriftenreihe Math. Sem. Inst. Angew. Math. Univ. Berlin'' , '''1'''  (1932)  pp. 95–140</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top">  G.M. Goluzin,  "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969)  (Translated from Russian)</TD></TR></table>
−
\frac{f( z) }{z }
 
−
  \right | \leq    \mathop{\rm ln} \
 
−
 
 
−
\frac{1 + | z | }{1 - | z | }
 
−
  ,\ | z | < 1;
 
−
$$
 
−
 
 
−
$$
 
−
\left | \mathop{\rm arg}  
 
−
\frac{zf ^ { \prime } ( z) }{f( z) }
 
−
  \right |
 
−
  \leq    \mathop{\rm ln}  
 
−
\frac{1 + | z | }{1 - | z | }
 
−
  ,\ \
 
−
| z | < 1.
 
−
$$
 
  
−
There are also rotation theorems in other classes of functions which realize a univalent conformal mapping of the disc or its exterior, and in classes of functions which are univalent in a multiply-connected domain (cf. [[#References|[5]]], [[#References|[3]]], [[Distortion theorems|Distortion theorems]]; [[Univalent function|Univalent function]]). Rotation theorems have also been extended to include the case of  $  p $-
 
−
valued functions (cf. addenda to [[#References|[5]]], and also [[Multivalent function|Multivalent function]]).
 
  
−
====References====
 
−
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  G.M. Goluzin,  "On distortion theorems in the theory of conformal mappings"  ''Mat. Sb.'' , '''1 (43)''' :  1  (1936)  pp. 127–135  (In Russian)  (German abstract)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  I.E. Bazilevich,  "Sur les théorèmes de Koebe–Bieberbach"  ''Mat. Sb.'' , '''1 (43)''' :  3  (1936)  pp. 283–292</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  J.A. Jenkins,  "Univalent functions and conformal mapping" , Springer  (1958)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top">  H. Grunsky,  "Neue Abschätzungen zur konformen Abbildung ein- und mehrfach zusammenhängender Bereiche"  ''Schriftenreihe Math. Sem. Inst. Angew. Math. Univ. Berlin'' , '''1'''  (1932)  pp. 95–140</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top">  G.M. Goluzin,  "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc.  (1969)  (Translated from Russian)</TD></TR></table>
 
  
 
====Comments====
 
====Comments====
−
For the class $  S $
+
For the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082680/r08268019.png" /> see also [[Bieberbach conjecture|Bieberbach conjecture]].
−
see also [[Bieberbach conjecture|Bieberbach conjecture]].
 
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  P.L. Duren,  "Univalent functions" , Springer  (1983)  pp. Sect. 10.11</TD></TR></table>
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  P.L. Duren,  "Univalent functions" , Springer  (1983)  pp. Sect. 10.11</TD></TR></table>

Revision as of 14:53, 7 June 2020

Theorems which characterize the change in the argument under a conformal mapping. Rotation theorems in the class 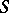of functions 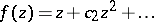which are regular and univalent in the disc 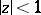give accurate estimates of the argument of the derivative for functions of this class:

(*)

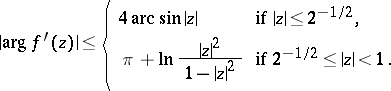Here one considers the branch of 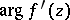that vanishes when 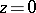. The upper and the lower bounds for 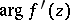given by the inequalities (*) are sharp for any in the disc 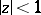. This rotation theorem was obtained by G.M. Goluzin [1], [5]; I.E. Bazilevich [2] was the first to show that the inequalities (*) are sharp for 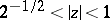; J.A. Jenkins [3] gave a complete analysis of the cases of equality in these estimates.

Rotation theorems in the class 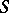is also the name given to estimates of 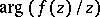and to estimates of expressions of the type

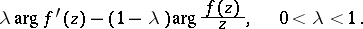The simplest estimates of this type in the class 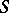are the sharp inequalities (the appropriate branches of the arguments are considered):

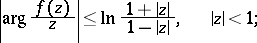There are also rotation theorems in other classes of functions which realize a univalent conformal mapping of the disc or its exterior, and in classes of functions which are univalent in a multiply-connected domain (cf. [5], [3], Distortion theorems; Univalent function). Rotation theorems have also been extended to include the case of 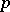-valued functions (cf. addenda to [5], and also Multivalent function).

References

[1] G.M. Goluzin, "On distortion theorems in the theory of conformal mappings" Mat. Sb. , 1 (43) : 1 (1936) pp. 127–135 (In Russian) (German abstract)
[2] I.E. Bazilevich, "Sur les théorèmes de Koebe–Bieberbach" Mat. Sb. , 1 (43) : 3 (1936) pp. 283–292
[3] J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958)
[4] H. Grunsky, "Neue Abschätzungen zur konformen Abbildung ein- und mehrfach zusammenhängender Bereiche" Schriftenreihe Math. Sem. Inst. Angew. Math. Univ. Berlin , 1 (1932) pp. 95–140
[5] G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)


Comments

For the class 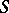see also Bieberbach conjecture.

References

[a1] P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11
How to Cite This Entry:
Rotation theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rotation_theorems&oldid=49412
This article was adapted from an original article by G.V. Kuz'mina (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Rotation_theorems&oldid=49412"