Difference between revisions of "Rational mapping"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48439 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A generalization of the concept of a [[Rational function|rational function]] on an [[Algebraic variety|algebraic variety]]. Namely, a rational mapping from an irreducible algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r0776101.png" /> to an algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r0776102.png" /> (both defined over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r0776103.png" />) is an equivalent class of pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r0776104.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r0776105.png" /> is a non-empty open subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r0776106.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r0776107.png" /> is a morphism from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r0776108.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r0776109.png" />. Two pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761011.png" /> are said to be equivalent if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761012.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761013.png" /> coincide on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761014.png" />. In particular, a rational mapping from a variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761015.png" /> to an affine line is a rational function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761016.png" />. For every rational mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761017.png" /> there is a pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761018.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761019.png" /> for all equivalent pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761021.png" /> is the restriction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761022.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761023.png" />. The open subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761024.png" /> is called the domain of regularity of the rational mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761025.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761026.png" /> is the image of the variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761027.png" /> (written <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761028.png" />) under <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761029.png" />. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761030.png" /> is a rational mapping of algebraic varieties and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761031.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761032.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761033.png" /> determines an imbedding of fields, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761034.png" />. Conversely, an imbedding of the fields of rational functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761035.png" /> determines a rational mapping from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761036.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761037.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761038.png" /> induces an isomorphism of the fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761039.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761040.png" /> of rational functions, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761041.png" /> is called a birational mapping. | |
| − | |||
| − | + | The set of points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761042.png" /> at which the rational mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761043.png" /> is not regular has codimension 1, in general. But if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761044.png" /> is complete and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761045.png" /> is smooth and irreducible, then this set has codimension at least 2. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761046.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761047.png" /> are complete irreducible varieties over an algebraically closed field of characteristic 0, then the rational mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761048.png" /> can be included in a commutative diagram (see [[#References|[2]]]): | |
| − | |||
| − | |||
| − | is | ||
| − | |||
| − | is | ||
| − | and | ||
| − | is | ||
| − | |||
| − | |||
| − | and | ||
| − | |||
| − | and | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761049.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761050.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761051.png" /> are morphisms of an algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761052.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761053.png" /> is a composite of monoidal transformations (cf. [[Monoidal transformation|Monoidal transformation]]). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761054.png" /> is a [[Birational mapping|birational mapping]] of complete non-singular surfaces, then there exists a diagram (*) in which both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761055.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761056.png" /> are composites of monoidal transformations with non-singular centres (Zariski's theorem), that is, every birational mapping of complete non-singular surface decomposes into monoidal transformations with non-singular centres and their inverses. In the case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077610/r07761057.png" />, the question of whether every birational mapping can be decomposed in this way is open (1990). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | are morphisms of an algebraic variety | ||
| − | and | ||
| − | is a composite of monoidal transformations (cf. [[Monoidal transformation|Monoidal transformation]]). If | ||
| − | is a [[Birational mapping|birational mapping]] of complete non-singular surfaces, then there exists a diagram (*) in which both | ||
| − | and | ||
| − | are composites of monoidal transformations with non-singular centres (Zariski's theorem), that is, every birational mapping of complete non-singular surface decomposes into monoidal transformations with non-singular centres and their inverses. In the case when | ||
| − | the question of whether every birational mapping can be decomposed in this way is open (1990). | ||
====References==== | ====References==== | ||
Revision as of 14:53, 7 June 2020
A generalization of the concept of a rational function on an algebraic variety. Namely, a rational mapping from an irreducible algebraic variety  to an algebraic variety
to an algebraic variety 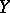 (both defined over a field
(both defined over a field  ) is an equivalent class of pairs
) is an equivalent class of pairs 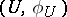 , where
, where  is a non-empty open subset of
is a non-empty open subset of 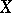 and
and 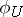 is a morphism from
is a morphism from  to
to 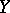 . Two pairs
. Two pairs  and
and 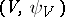 are said to be equivalent if
are said to be equivalent if 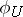 and
and 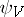 coincide on
coincide on 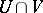 . In particular, a rational mapping from a variety
. In particular, a rational mapping from a variety 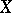 to an affine line is a rational function on
to an affine line is a rational function on 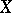 . For every rational mapping
. For every rational mapping 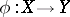 there is a pair
there is a pair 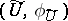 such that
such that 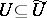 for all equivalent pairs
for all equivalent pairs 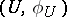 and
and 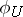 is the restriction of
is the restriction of 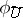 to
to 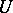 . The open subset
. The open subset 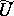 is called the domain of regularity of the rational mapping
is called the domain of regularity of the rational mapping 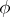 , and
, and 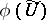 is the image of the variety
is the image of the variety 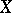 (written
(written 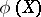 ) under
) under 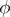 .
.
If 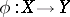 is a rational mapping of algebraic varieties and
is a rational mapping of algebraic varieties and  is dense in
is dense in 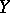 , then
, then 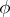 determines an imbedding of fields,
determines an imbedding of fields, 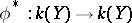 . Conversely, an imbedding of the fields of rational functions
. Conversely, an imbedding of the fields of rational functions 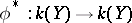 determines a rational mapping from
determines a rational mapping from 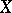 to
to 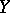 . If
. If 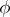 induces an isomorphism of the fields
induces an isomorphism of the fields 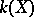 and
and 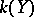 of rational functions, then
of rational functions, then 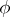 is called a birational mapping.
is called a birational mapping.
The set of points of 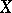 at which the rational mapping
at which the rational mapping  is not regular has codimension 1, in general. But if
is not regular has codimension 1, in general. But if 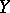 is complete and
is complete and 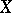 is smooth and irreducible, then this set has codimension at least 2. If
is smooth and irreducible, then this set has codimension at least 2. If 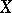 and
and 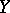 are complete irreducible varieties over an algebraically closed field of characteristic 0, then the rational mapping
are complete irreducible varieties over an algebraically closed field of characteristic 0, then the rational mapping 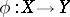 can be included in a commutative diagram (see [2]):
can be included in a commutative diagram (see [2]):
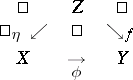 | (*) |
where 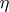 ,
, 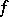 are morphisms of an algebraic variety
are morphisms of an algebraic variety 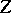 and
and 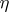 is a composite of monoidal transformations (cf. Monoidal transformation). If
is a composite of monoidal transformations (cf. Monoidal transformation). If 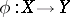 is a birational mapping of complete non-singular surfaces, then there exists a diagram (*) in which both
is a birational mapping of complete non-singular surfaces, then there exists a diagram (*) in which both 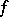 and
and 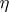 are composites of monoidal transformations with non-singular centres (Zariski's theorem), that is, every birational mapping of complete non-singular surface decomposes into monoidal transformations with non-singular centres and their inverses. In the case when
are composites of monoidal transformations with non-singular centres (Zariski's theorem), that is, every birational mapping of complete non-singular surface decomposes into monoidal transformations with non-singular centres and their inverses. In the case when 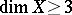 , the question of whether every birational mapping can be decomposed in this way is open (1990).
, the question of whether every birational mapping can be decomposed in this way is open (1990).
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
| [2] | H. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero I" Ann. of Math. , 79 : 1–2 (1964) pp. 109–326 MR0199184 Zbl 0122.38603 |
Rational mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_mapping&oldid=49390