Difference between revisions of "Principal curvature"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48288 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | The [[Normal curvature|normal curvature]] of a surface in a principal direction, i.e. in a direction in which it assumes an extremal value. The principal curvatures <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p0746601.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p0746602.png" /> are the roots of the quadratic equation |
| − | p0746601.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p0746603.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p0746604.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p0746605.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p0746606.png" /> are the coefficients of the [[First fundamental form|first fundamental form]], while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p0746607.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p0746608.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p0746609.png" /> are the coefficients of the [[Second fundamental form|second fundamental form]] of the surface, computed at the given point. | |
| − | and | ||
| − | are the | ||
| − | + | The half-sum of the principal curvatures <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466011.png" /> of the surface gives the [[Mean curvature|mean curvature]], while their product is equal to the [[Gaussian curvature|Gaussian curvature]] of the surface. Equation (*) may be written as | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466012.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466013.png" /> is the mean, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466014.png" /> is the Gaussian curvature of the surface at the given point. | |
| − | |||
| − | |||
| − | + | The principal curvatures <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466016.png" /> are connected with the normal curvature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466017.png" />, taken in an arbitrary direction, by means of Euler's formula: | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466018.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466019.png" /> is the angle formed by the selected direction with the principal direction for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466020.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | In the case of an | + | In the case of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466021.png" />-dimensional submanifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466022.png" /> of Euclidean <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466023.png" />-space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466024.png" /> principal curvatures and principal directions are defined as follows. |
| − | dimensional submanifold | ||
| − | of Euclidean | ||
| − | space | ||
| − | principal curvatures and principal directions are defined as follows. | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466025.png" /> be a unit normal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466026.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466027.png" />. The Weingarten mapping (shape operator) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466028.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466029.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466030.png" /> in direction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466031.png" /> is given by the tangential part of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466032.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466033.png" /> is the [[Covariant differential|covariant differential]] in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466035.png" /> is a local extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466036.png" /> to a unit normal vector field. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466037.png" /> does not depend on the chosen extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466038.png" />. The principal curvatures of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466039.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466040.png" /> in direction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466041.png" /> are given by the eigen values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466042.png" />, the principal directions by its eigen directions. The (normalized) elementary symmetric functions of the eigen values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466043.png" /> define the higher mean curvatures of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466044.png" />, which include as extremal cases the mean curvature as the trace of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074660/p07466045.png" /> and the Lipschitz–Killing curvature as its determinant. |
| − | be a unit normal to | ||
| − | at | ||
| − | The Weingarten mapping (shape operator) | ||
| − | of | ||
| − | at | ||
| − | in direction | ||
| − | is given by the tangential part of | ||
| − | where | ||
| − | is the [[Covariant differential|covariant differential]] in | ||
| − | and | ||
| − | is a local extension of | ||
| − | to a unit normal vector field. | ||
| − | does not depend on the chosen extension of | ||
| − | The principal curvatures of | ||
| − | at | ||
| − | in direction | ||
| − | are given by the eigen values of | ||
| − | the principal directions by its eigen directions. The (normalized) elementary symmetric functions of the eigen values of | ||
| − | define the higher mean curvatures of | ||
| − | which include as extremal cases the mean curvature as the trace of | ||
| − | and the Lipschitz–Killing curvature as its determinant. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 145</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) pp. 25; 60</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> B. O'Neill, "Elementary differential geometry" , Acad. Press (1966)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> M. Spivak, "A comprehensive introduction to differential geometry" , '''1979''' , Publish or Perish pp. 1–5</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 145</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) pp. 25; 60</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> B. O'Neill, "Elementary differential geometry" , Acad. Press (1966)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> M. Spivak, "A comprehensive introduction to differential geometry" , '''1979''' , Publish or Perish pp. 1–5</TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
The normal curvature of a surface in a principal direction, i.e. in a direction in which it assumes an extremal value. The principal curvatures 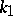 and
and 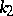 are the roots of the quadratic equation
are the roots of the quadratic equation
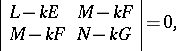 | (*) |
where 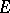 ,
, 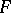 and
and  are the coefficients of the first fundamental form, while
are the coefficients of the first fundamental form, while 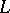 ,
, 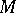 and
and 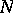 are the coefficients of the second fundamental form of the surface, computed at the given point.
are the coefficients of the second fundamental form of the surface, computed at the given point.
The half-sum of the principal curvatures 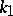 and
and 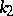 of the surface gives the mean curvature, while their product is equal to the Gaussian curvature of the surface. Equation (*) may be written as
of the surface gives the mean curvature, while their product is equal to the Gaussian curvature of the surface. Equation (*) may be written as
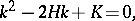 |
where 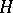 is the mean, and
is the mean, and 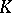 is the Gaussian curvature of the surface at the given point.
is the Gaussian curvature of the surface at the given point.
The principal curvatures 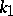 and
and 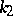 are connected with the normal curvature
are connected with the normal curvature 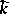 , taken in an arbitrary direction, by means of Euler's formula:
, taken in an arbitrary direction, by means of Euler's formula:
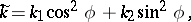 |
where 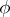 is the angle formed by the selected direction with the principal direction for
is the angle formed by the selected direction with the principal direction for 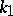 .
.
Comments
In the case of an 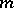 -dimensional submanifold
-dimensional submanifold 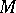 of Euclidean
of Euclidean  -space
-space  principal curvatures and principal directions are defined as follows.
principal curvatures and principal directions are defined as follows.
Let 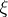 be a unit normal to
be a unit normal to 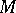 at
at  . The Weingarten mapping (shape operator)
. The Weingarten mapping (shape operator) 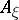 of
of 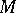 at
at 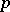 in direction
in direction 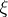 is given by the tangential part of
is given by the tangential part of  , where
, where  is the covariant differential in
is the covariant differential in  and
and 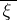 is a local extension of
is a local extension of 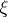 to a unit normal vector field.
to a unit normal vector field. 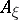 does not depend on the chosen extension of
does not depend on the chosen extension of 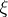 . The principal curvatures of
. The principal curvatures of 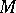 at
at 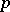 in direction
in direction 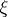 are given by the eigen values of
are given by the eigen values of 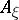 , the principal directions by its eigen directions. The (normalized) elementary symmetric functions of the eigen values of
, the principal directions by its eigen directions. The (normalized) elementary symmetric functions of the eigen values of  define the higher mean curvatures of
define the higher mean curvatures of 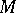 , which include as extremal cases the mean curvature as the trace of
, which include as extremal cases the mean curvature as the trace of 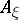 and the Lipschitz–Killing curvature as its determinant.
and the Lipschitz–Killing curvature as its determinant.
References
| [a1] | N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) |
| [a2] | B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973) |
| [a3] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a4] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963) |
| [a5] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 145 |
| [a6] | H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) pp. 25; 60 |
| [a7] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
| [a8] | B. O'Neill, "Elementary differential geometry" , Acad. Press (1966) |
| [a9] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 1–5 |
Principal curvature. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principal_curvature&oldid=49376