Difference between revisions of "Parametrix method"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48129 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
One of the methods for studying boundary value problems for differential equations with variable coefficients by means of integral equations. | One of the methods for studying boundary value problems for differential equations with variable coefficients by means of integral equations. | ||
| − | Suppose that in some region | + | Suppose that in some region <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p0715701.png" /> of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p0715702.png" />-dimensional Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p0715703.png" /> one considers an elliptic differential operator (cf. [[Elliptic partial differential equation|Elliptic partial differential equation]]) of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p0715704.png" />, |
| − | of the | ||
| − | dimensional Euclidean space | ||
| − | one considers an elliptic differential operator (cf. [[Elliptic partial differential equation|Elliptic partial differential equation]]) of order | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p0715705.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | In (1) the symbol | + | In (1) the symbol <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p0715706.png" /> is a multi-index, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p0715707.png" />, where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p0715708.png" /> are non-negative integers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p0715709.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157011.png" />. With every operator (1) there is associated the homogeneous elliptic operator |
| − | is a multi-index, | ||
| − | where the | ||
| − | are non-negative integers, | ||
| − | |||
| − | |||
| − | With every operator (1) there is associated the homogeneous elliptic operator | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157012.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | with constant coefficients, where | + | with constant coefficients, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157013.png" /> is an arbitrary fixed point. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157014.png" /> denote a [[Fundamental solution|fundamental solution]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157015.png" /> depending parametrically on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157016.png" />. Then the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157017.png" /> is called the parametrix of the operator (1) with a singularity at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157018.png" />. |
| − | is an arbitrary fixed point. Let | ||
| − | denote a [[Fundamental solution|fundamental solution]] of | ||
| − | depending parametrically on | ||
| − | Then the function | ||
| − | is called the parametrix of the operator (1) with a singularity at | ||
In particular, for the second-order elliptic operator | In particular, for the second-order elliptic operator | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157019.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | one can take as parametrix with singularity at | + | one can take as parametrix with singularity at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157020.png" /> the Levi function |
| − | the Levi function | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157021.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | In (2), | + | In (2), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157023.png" /> is the determinant of the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157024.png" />, |
| − | |||
| − | is the determinant of the matrix | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157025.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | and | + | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157026.png" /> are the elements of the matrix inverse to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157027.png" />. |
| − | are the elements of the matrix inverse to | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157028.png" /> be the integral operator |
| − | be the integral operator | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157029.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table> | |
| − | |||
| − | |||
| − | acting on functions from | + | acting on functions from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157030.png" /> and let |
| − | and let | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157031.png" /></td> </tr></table> | |
| − | |||
| − | |||
Since, by definition of a fundamental solution, | Since, by definition of a fundamental solution, | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157032.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157033.png" /> is the identity operator, one has |
| − | is the identity operator, one has | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157034.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | This equality indicates that for every sufficiently-smooth function | + | This equality indicates that for every sufficiently-smooth function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157035.png" /> of compact support in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157036.png" /> there is a representation |
| − | of compact support in | ||
| − | there is a representation | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157037.png" /></td> <td valign="top" style="width:5%;text-align:right;">(4)</td></tr></table> | |
| − | |||
| − | |||
Moreover, if | Moreover, if | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157038.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | then | + | then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157039.png" /> is a solution of the equation |
| − | is a solution of the equation | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157040.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | Thus, the question of the local solvability of | + | Thus, the question of the local solvability of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157041.png" /> reduces to that of invertibility of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157042.png" />. |
| − | reduces to that of invertibility of | ||
| − | If one applies | + | If one applies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157043.png" /> to functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157044.png" /> that vanish outside a ball of radius <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157045.png" /> with centre at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157046.png" />, then for a sufficiently small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157047.png" /> the norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157048.png" /> can be made smaller than one. Then the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157049.png" /> exists; consequently, also <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157050.png" /> exists, which is the inverse operator to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157051.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157052.png" /> is an integral operator with as kernel a fundamental solution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157053.png" />. |
| − | to functions | ||
| − | that vanish outside a ball of radius | ||
| − | with centre at | ||
| − | then for a sufficiently small | ||
| − | the norm of | ||
| − | can be made smaller than one. Then the operator | ||
| − | exists; consequently, also | ||
| − | exists, which is the inverse operator to | ||
| − | Here | ||
| − | is an integral operator with as kernel a fundamental solution of | ||
| − | The name parametrix is sometimes given not only to the function | + | The name parametrix is sometimes given not only to the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157054.png" />, but also to the integral operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157055.png" /> with the kernel <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157056.png" />, as defined by (3). |
| − | but also to the integral operator | ||
| − | with the kernel | ||
| − | as defined by (3). | ||
| − | In the theory of pseudo-differential operators, instead of | + | In the theory of pseudo-differential operators, instead of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157057.png" /> a parametrix of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157058.png" /> is defined as an operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157059.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157060.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157061.png" /> are integral operators with infinitely-differentiable kernels (cf. [[Pseudo-differential operator|Pseudo-differential operator]]). If only <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157062.png" /> (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157063.png" />) is such an operator, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157064.png" /> is called a left (or right) parametrix of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157065.png" />. In other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157066.png" /> in (4) is a left parametrix if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157067.png" /> in this equality has an infinitely-differentiable kernel. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157068.png" /> has a left parametrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157069.png" /> and a right parametrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157070.png" />, then each of them is a parametrix. The existence of a parametrix has been proved for hypo-elliptic pseudo-differential operators (see [[#References|[3]]]). |
| − | a parametrix of | ||
| − | is defined as an operator | ||
| − | such that | ||
| − | and | ||
| − | are integral operators with infinitely-differentiable kernels (cf. [[Pseudo-differential operator|Pseudo-differential operator]]). If only | ||
| − | or | ||
| − | is such an operator, then | ||
| − | is called a left (or right) parametrix of | ||
| − | In other words, | ||
| − | in (4) is a left parametrix if | ||
| − | in this equality has an infinitely-differentiable kernel. If | ||
| − | has a left parametrix | ||
| − | and a right parametrix | ||
| − | then each of them is a parametrix. The existence of a parametrix has been proved for hypo-elliptic pseudo-differential operators (see [[#References|[3]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L. Hörmander, , ''Pseudo-differential operators'' , Moscow (1967) (In Russian; translated from English)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L. Hörmander, , ''Pseudo-differential operators'' , Moscow (1967) (In Russian; translated from English)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| − | The operator | + | The operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157071.png" /> is called the principal part of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071570/p07157072.png" />, cf. [[Principal part of a differential operator|Principal part of a differential operator]]. The parametrix method was anticipated in two fundamental papers by E.E. Levi [[#References|[a1]]], [[#References|[a2]]]. The same procedure is also applicable for constructing the fundamental solution of a parabolic equation with variable coefficients (see, e.g., [[#References|[a3]]]). |
| − | is called the principal part of | ||
| − | cf. [[Principal part of a differential operator|Principal part of a differential operator]]. The parametrix method was anticipated in two fundamental papers by E.E. Levi [[#References|[a1]]], [[#References|[a2]]]. The same procedure is also applicable for constructing the fundamental solution of a parabolic equation with variable coefficients (see, e.g., [[#References|[a3]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.E. Levi, "Sulle equazioni lineari alle derivate parziali totalmente ellittiche" ''Rend. R. Acc. Lincei, Classe Sci. (V)'' , '''16''' (1907)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E.E. Levi, "Sulle equazioni lineari totalmente ellittiche alle derivate parziali" ''Rend. Circ. Mat. Palermo'' , '''24''' (1907) pp. 275–317</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> L.V. Hörmander, "The analysis of linear partial differential operators" , '''1–4''' , Springer (1983–1985) pp. Chapts. 7; 18</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.E. Levi, "Sulle equazioni lineari alle derivate parziali totalmente ellittiche" ''Rend. R. Acc. Lincei, Classe Sci. (V)'' , '''16''' (1907)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E.E. Levi, "Sulle equazioni lineari totalmente ellittiche alle derivate parziali" ''Rend. Circ. Mat. Palermo'' , '''24''' (1907) pp. 275–317</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> L.V. Hörmander, "The analysis of linear partial differential operators" , '''1–4''' , Springer (1983–1985) pp. Chapts. 7; 18</TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
One of the methods for studying boundary value problems for differential equations with variable coefficients by means of integral equations.
Suppose that in some region  of the
of the  -dimensional Euclidean space
-dimensional Euclidean space  one considers an elliptic differential operator (cf. Elliptic partial differential equation) of order
one considers an elliptic differential operator (cf. Elliptic partial differential equation) of order  ,
,
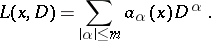 | (1) |
In (1) the symbol  is a multi-index,
is a multi-index,  , where the
, where the  are non-negative integers,
are non-negative integers,  ,
,  ,
, 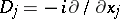 . With every operator (1) there is associated the homogeneous elliptic operator
. With every operator (1) there is associated the homogeneous elliptic operator
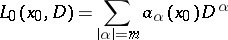 |
with constant coefficients, where  is an arbitrary fixed point. Let
is an arbitrary fixed point. Let  denote a fundamental solution of
denote a fundamental solution of 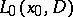 depending parametrically on
depending parametrically on  . Then the function
. Then the function  is called the parametrix of the operator (1) with a singularity at
is called the parametrix of the operator (1) with a singularity at 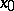 .
.
In particular, for the second-order elliptic operator
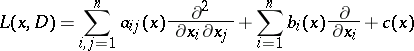 |
one can take as parametrix with singularity at 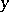 the Levi function
the Levi function
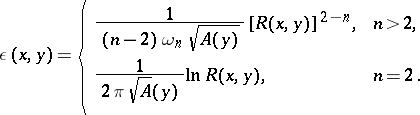 | (2) |
In (2),  ,
,  is the determinant of the matrix
is the determinant of the matrix  ,
,
 |
and  are the elements of the matrix inverse to
are the elements of the matrix inverse to  .
.
Let  be the integral operator
be the integral operator
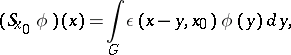 | (3) |
acting on functions from  and let
and let
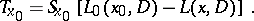 |
Since, by definition of a fundamental solution,
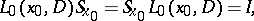 |
where 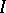 is the identity operator, one has
is the identity operator, one has
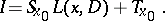 |
This equality indicates that for every sufficiently-smooth function 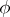 of compact support in
of compact support in  there is a representation
there is a representation
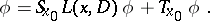 | (4) |
Moreover, if
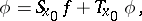 |
then 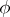 is a solution of the equation
is a solution of the equation
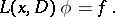 |
Thus, the question of the local solvability of 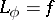 reduces to that of invertibility of
reduces to that of invertibility of 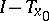 .
.
If one applies  to functions
to functions  that vanish outside a ball of radius
that vanish outside a ball of radius  with centre at
with centre at  , then for a sufficiently small
, then for a sufficiently small  the norm of
the norm of  can be made smaller than one. Then the operator
can be made smaller than one. Then the operator 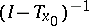 exists; consequently, also
exists; consequently, also  exists, which is the inverse operator to
exists, which is the inverse operator to 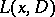 . Here
. Here 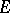 is an integral operator with as kernel a fundamental solution of
is an integral operator with as kernel a fundamental solution of 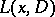 .
.
The name parametrix is sometimes given not only to the function 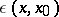 , but also to the integral operator
, but also to the integral operator  with the kernel
with the kernel 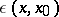 , as defined by (3).
, as defined by (3).
In the theory of pseudo-differential operators, instead of 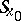 a parametrix of
a parametrix of  is defined as an operator
is defined as an operator 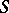 such that
such that  and
and 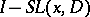 are integral operators with infinitely-differentiable kernels (cf. Pseudo-differential operator). If only
are integral operators with infinitely-differentiable kernels (cf. Pseudo-differential operator). If only 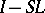 (or
(or 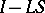 ) is such an operator, then
) is such an operator, then 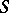 is called a left (or right) parametrix of
is called a left (or right) parametrix of 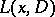 . In other words,
. In other words, 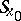 in (4) is a left parametrix if
in (4) is a left parametrix if  in this equality has an infinitely-differentiable kernel. If
in this equality has an infinitely-differentiable kernel. If 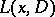 has a left parametrix
has a left parametrix 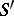 and a right parametrix
and a right parametrix  , then each of them is a parametrix. The existence of a parametrix has been proved for hypo-elliptic pseudo-differential operators (see [3]).
, then each of them is a parametrix. The existence of a parametrix has been proved for hypo-elliptic pseudo-differential operators (see [3]).
References
| [1] | L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964) |
| [2] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [3] | L. Hörmander, , Pseudo-differential operators , Moscow (1967) (In Russian; translated from English) |
Comments
The operator  is called the principal part of
is called the principal part of 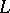 , cf. Principal part of a differential operator. The parametrix method was anticipated in two fundamental papers by E.E. Levi [a1], [a2]. The same procedure is also applicable for constructing the fundamental solution of a parabolic equation with variable coefficients (see, e.g., [a3]).
, cf. Principal part of a differential operator. The parametrix method was anticipated in two fundamental papers by E.E. Levi [a1], [a2]. The same procedure is also applicable for constructing the fundamental solution of a parabolic equation with variable coefficients (see, e.g., [a3]).
References
| [a1] | E.E. Levi, "Sulle equazioni lineari alle derivate parziali totalmente ellittiche" Rend. R. Acc. Lincei, Classe Sci. (V) , 16 (1907) |
| [a2] | E.E. Levi, "Sulle equazioni lineari totalmente ellittiche alle derivate parziali" Rend. Circ. Mat. Palermo , 24 (1907) pp. 275–317 |
| [a3] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
| [a4] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1–4 , Springer (1983–1985) pp. Chapts. 7; 18 |
Parametrix method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parametrix_method&oldid=49355