Difference between revisions of "Multinomial distribution"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 47928 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''polynomial distribution'' | ''polynomial distribution'' | ||
| Line 17: | Line 5: | ||
[[Category:Distribution theory]] | [[Category:Distribution theory]] | ||
| − | The joint distribution of random variables | + | The joint distribution of random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m0653301.png" /> that is defined for any set of non-negative integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m0653302.png" /> satisfying the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m0653303.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m0653304.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m0653305.png" />, by the formula |
| − | that is defined for any set of non-negative integers | ||
| − | satisfying the condition | ||
| − | |||
| − | |||
| − | by the formula | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m0653306.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m0653307.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m0653308.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m0653309.png" />) are the parameters of the distribution. A multinomial distribution is a multivariate discrete distribution, namely the distribution for the random vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533010.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533011.png" /> (this distribution is in essence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533012.png" />-dimensional, since it is degenerate in the Euclidean space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533013.png" /> dimensions). A multinomial distribution is a natural generalization of a [[Binomial distribution|binomial distribution]] and coincides with the latter for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533014.png" />. The name of the distribution is given because the probability (*) is the general term in the expansion of the multinomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533015.png" />. The multinomial distribution appears in the following probability scheme. Each of the random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533016.png" /> is the number of occurrences of one of the mutually exclusive events <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533017.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533018.png" />, in repeated independent trials. If in each trial the probability of event <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533019.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533021.png" />, then the probability (*) is equal to the probability that in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533022.png" /> trials the events <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533023.png" /> will appear <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533024.png" /> times, respectively. Each of the random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533025.png" /> has a binomial distribution with mathematical expectation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533026.png" /> and variance <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533027.png" />. |
| − | |||
| − | |||
| − | are the parameters of the distribution. A multinomial distribution is a multivariate discrete distribution, namely the distribution for the random vector | ||
| − | with | ||
| − | this distribution is in essence | ||
| − | dimensional, since it is degenerate in the Euclidean space of | ||
| − | dimensions). A multinomial distribution is a natural generalization of a [[Binomial distribution|binomial distribution]] and coincides with the latter for | ||
| − | The name of the distribution is given because the probability (*) is the general term in the expansion of the multinomial | ||
| − | The multinomial distribution appears in the following probability scheme. Each of the random variables | ||
| − | is the number of occurrences of one of the mutually exclusive events | ||
| − | |||
| − | in repeated independent trials. If in each trial the probability of event | ||
| − | is | ||
| − | |||
| − | then the probability (*) is equal to the probability that in | ||
| − | trials the events | ||
| − | will appear | ||
| − | times, respectively. Each of the random variables | ||
| − | has a binomial distribution with mathematical expectation | ||
| − | and variance | ||
| − | The random vector | + | The random vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533028.png" /> has mathematical expectation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533029.png" /> and covariance matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533030.png" />, where |
| − | has mathematical expectation | ||
| − | and covariance matrix | ||
| − | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533031.png" /></td> </tr></table> | |
| − | |||
| − | (the rank of the matrix | + | (the rank of the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533032.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533033.png" /> because <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533034.png" />). The characteristic function of a multinomial distribution is |
| − | is | ||
| − | because | ||
| − | The characteristic function of a multinomial distribution is | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533035.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | For | + | For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533036.png" />, the distribution of the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533037.png" /> with normalized components |
| − | the distribution of the vector | ||
| − | with normalized components | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533038.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
tends to a certain multivariate [[Normal distribution|normal distribution]], while the distribution of the sum | tends to a certain multivariate [[Normal distribution|normal distribution]], while the distribution of the sum | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533039.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | (which is used in mathematical statistics to construct the [[Chi-squared distribution| "chi-squared" test]]) tends to the [[Chi-squared test| "chi-squared" distribution]] with | + | (which is used in mathematical statistics to construct the [[Chi-squared distribution| "chi-squared" test]]) tends to the [[Chi-squared test| "chi-squared" distribution]] with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065330/m06533040.png" /> degrees of freedom. |
| − | degrees of freedom. | ||
====References==== | ====References==== | ||
| Line 94: | Line 35: | ||
====Comments==== | ====Comments==== | ||
| + | |||
====References==== | ====References==== | ||
Revision as of 14:32, 7 June 2020
polynomial distribution
2020 Mathematics Subject Classification: Primary: 60E99 [MSN][ZBL]
The joint distribution of random variables  that is defined for any set of non-negative integers
that is defined for any set of non-negative integers  satisfying the condition
satisfying the condition  ,
,  ,
,  , by the formula
, by the formula
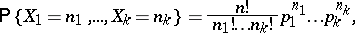 | (*) |
where  (
( ,
,  ) are the parameters of the distribution. A multinomial distribution is a multivariate discrete distribution, namely the distribution for the random vector
) are the parameters of the distribution. A multinomial distribution is a multivariate discrete distribution, namely the distribution for the random vector 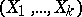 with
with 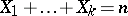 (this distribution is in essence
(this distribution is in essence 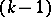 -dimensional, since it is degenerate in the Euclidean space of
-dimensional, since it is degenerate in the Euclidean space of 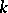 dimensions). A multinomial distribution is a natural generalization of a binomial distribution and coincides with the latter for
dimensions). A multinomial distribution is a natural generalization of a binomial distribution and coincides with the latter for 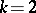 . The name of the distribution is given because the probability (*) is the general term in the expansion of the multinomial
. The name of the distribution is given because the probability (*) is the general term in the expansion of the multinomial 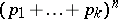 . The multinomial distribution appears in the following probability scheme. Each of the random variables
. The multinomial distribution appears in the following probability scheme. Each of the random variables  is the number of occurrences of one of the mutually exclusive events
is the number of occurrences of one of the mutually exclusive events 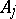 ,
, 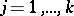 , in repeated independent trials. If in each trial the probability of event
, in repeated independent trials. If in each trial the probability of event  is
is  ,
,  , then the probability (*) is equal to the probability that in
, then the probability (*) is equal to the probability that in  trials the events
trials the events  will appear
will appear  times, respectively. Each of the random variables
times, respectively. Each of the random variables 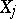 has a binomial distribution with mathematical expectation
has a binomial distribution with mathematical expectation 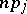 and variance
and variance  .
.
The random vector 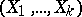 has mathematical expectation
has mathematical expectation 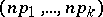 and covariance matrix
and covariance matrix 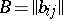 , where
, where
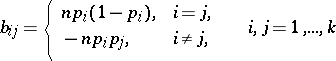 |
(the rank of the matrix 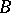 is
is  because
because 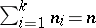 ). The characteristic function of a multinomial distribution is
). The characteristic function of a multinomial distribution is
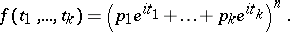 |
For 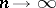 , the distribution of the vector
, the distribution of the vector 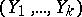 with normalized components
with normalized components
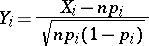 |
tends to a certain multivariate normal distribution, while the distribution of the sum
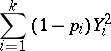 |
(which is used in mathematical statistics to construct the "chi-squared" test) tends to the "chi-squared" distribution with  degrees of freedom.
degrees of freedom.
References
| [C] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) MR0016588 Zbl 0063.01014 |
Comments
References
| [JK] | N.L. Johnson, S. Kotz, "Discrete distributions" , Wiley (1969) MR0268996 Zbl 0292.62009 |
Multinomial distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multinomial_distribution&oldid=49316