Difference between revisions of "Hilbert-Schmidt operator"
Ulf Rehmann (talk | contribs) m (moved Hilbert–Schmidt operator to Hilbert-Schmidt operator: ascii title) |
m (→Comments: better) |
||
| Line 26: | Line 26: | ||
====Comments==== | ====Comments==== | ||
| − | The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735022.png" />-numbers or singular | + | The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735022.png" />-numbers or [[singular value]]s of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735023.png" /> are the (positive) eigen values of the self-adjoint operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735024.png" />. Instead of Hilbert–Schmidt operator one also says "operator of Hilbert–Schmidt class" . A bounded operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735025.png" /> on a Hilbert space is said to be of trace class if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735026.png" /> for arbitrary complete orthonormal systems <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735028.png" />. Equivalently, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735029.png" /> is of trace class if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735030.png" />. The trace of such an operator is defined as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735031.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735032.png" /> is any orthonormal basis. The product of two Hilbert–Schmidt operators is of trace class and the converse is also true. |
The norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735033.png" /> in the above article is not the usual operator norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735034.png" /> but its [[Hilbert–Schmidt norm|Hilbert–Schmidt norm]]. | The norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735033.png" /> in the above article is not the usual operator norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047350/h04735034.png" /> but its [[Hilbert–Schmidt norm|Hilbert–Schmidt norm]]. | ||
Revision as of 17:22, 10 May 2020
An operator  acting on a Hilbert space
acting on a Hilbert space  such that for any orthonormal basis
such that for any orthonormal basis  in
in  the following condition is met:
the following condition is met:
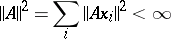 |
(however, this need be true for some basis only). A Hilbert–Schmidt operator is a compact operator for which the condition
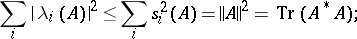 |
applies to its  -numbers
-numbers  and its eigen values
and its eigen values  ; here
; here 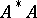 is a trace-class operator (
is a trace-class operator (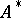 is the adjoint of
is the adjoint of  and
and 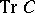 is the trace of an operator
is the trace of an operator 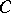 ). The set of all Hilbert–Schmidt operators on a fixed space
). The set of all Hilbert–Schmidt operators on a fixed space 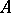 forms a Hilbert space with scalar product
forms a Hilbert space with scalar product
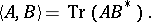 |
If 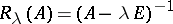 is the resolvent of
is the resolvent of 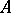 and
and
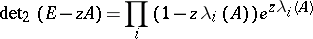 |
is its regularized characteristic determinant, then the Carleman inequality
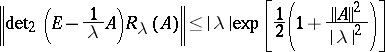 |
holds.
A typical representative of a Hilbert–Schmidt operator is a Hilbert–Schmidt integral operator (which explains the origin of the name).
Comments
The  -numbers or singular values of
-numbers or singular values of  are the (positive) eigen values of the self-adjoint operator
are the (positive) eigen values of the self-adjoint operator 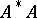 . Instead of Hilbert–Schmidt operator one also says "operator of Hilbert–Schmidt class" . A bounded operator
. Instead of Hilbert–Schmidt operator one also says "operator of Hilbert–Schmidt class" . A bounded operator 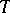 on a Hilbert space is said to be of trace class if
on a Hilbert space is said to be of trace class if  for arbitrary complete orthonormal systems
for arbitrary complete orthonormal systems 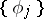 ,
, 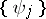 . Equivalently,
. Equivalently, 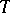 is of trace class if
is of trace class if 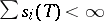 . The trace of such an operator is defined as
. The trace of such an operator is defined as 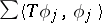 , where
, where 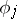 is any orthonormal basis. The product of two Hilbert–Schmidt operators is of trace class and the converse is also true.
is any orthonormal basis. The product of two Hilbert–Schmidt operators is of trace class and the converse is also true.
The norm 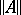 in the above article is not the usual operator norm of
in the above article is not the usual operator norm of 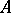 but its Hilbert–Schmidt norm.
but its Hilbert–Schmidt norm.
References
| [a1] | M. Reed, B. Simon, "Methods of modern mathematical physics" , 1. Functional analysis , Acad. Press (1972) |
| [a2] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1977) |
| [a3] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1981) (Translated from Russian) |
Hilbert-Schmidt operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert-Schmidt_operator&oldid=45835