Difference between revisions of "Stability theorems in algebraic K-theory"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex done) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|done}} | |
| − | + | Assertions on the invariance of the groups $ K _{i} (R) $ | |
| + | or their subgroups, given certain special extensions of the ground ring $ R $( | ||
| + | see [[Algebraic K-theory|Algebraic $ K $- | ||
| + | theory]]). | ||
| − | + | The following are the best-known stability theorems. Let $ R $ | |
| + | be a regular ring (cf. [[Regular ring (in commutative algebra)|Regular ring (in commutative algebra)]]) and let $ R[t _{1} \dots t _{n} ] $ | ||
| + | be the ring of polynomials in the variables $ t _{1} \dots t _{n} $ | ||
| + | over $ R $. | ||
| + | The stability theorem for Whitehead groups under the transfer from $ R $ | ||
| + | to $ R[t _{1} \dots t _{n} ] $, | ||
| + | [[#References|[1]]], states that the natural homomorphism imbedding $ R $ | ||
| + | in $ R[t _{1} \dots t _{n} ] $ | ||
| + | induces an isomorphism between $ K _{1} (R) $ | ||
| + | and $ K _{1} (R[t _{1} \dots t _{n} ]) $( | ||
| + | cf. also [[Whitehead group|Whitehead group]]). | ||
| − | + | In the case of a skew-field $ R $ | |
| + | that is finite-dimensional over its centre $ Z(R) $, | ||
| + | one can define a reduced-norm homomorphism $ \mathop{\rm Nrd}\nolimits _{R} : \ R ^ \star \rightarrow Z(R) ^ \star $ | ||
| + | of the multiplicative group $ R ^ \star $ | ||
| + | of $ R $ | ||
| + | into the multiplicative group $ Z(R) ^ \star $ | ||
| + | of its centre. The kernel of this homomorphism, usually written as $ \mathop{\rm SL}\nolimits (1,\ R) $, | ||
| + | determines the reduced Whitehead group $ SK _{1} (R) $ | ||
| + | of $ R $: | ||
| + | $$ | ||
| + | SK _{1} (R) \simeq { \mathop{\rm SL}\nolimits (1,\ R)} / {[R ^ \star ,\ R ^ \star ]} | ||
| + | $$( | ||
| + | see [[Special linear group|Special linear group]]), which is a subgroup in $ K _{1} (R) $. | ||
| + | If $ Z(R)(t _{1} \dots t _{n} ) $ | ||
| + | is the field of rational functions in $ t _{1} \dots t _{n} $ | ||
| + | over $ Z(R) $, | ||
| + | then the algebra $$ | ||
| + | R(t _{1} \dots t _{n} ) = R \otimes _{Z(R)} Z(R)(t _{1} \dots t _{n} ) | ||
| + | $$ | ||
| + | is a skew-field, and the natural imbedding $ \phi _ {t _{1} \dots t _ n} $ | ||
| + | of $ R $ | ||
| + | in $ R(t _{1} \dots t _{n} ) $ | ||
| + | induces a homomorphism $$ | ||
| + | \psi _ {t _{1} \dots t _ n} ^ \prime : \ SK _{1} (R) \rightarrow | ||
| + | SK _{1} (R(t _{1} \dots t _{n} )). | ||
| + | $$ | ||
| + | The stability theorem for reduced Whitehead groups states that the homomorphism $ \psi _ {t _{1} \dots t _ n} ^ \prime $ | ||
| + | is bijective ([[#References|[2]]], see also [[#References|[3]]]). Similar statements are also true in unitary and spinor algebraic $ K $- | ||
| + | theories [[#References|[4]]], [[#References|[5]]]. | ||
| − | + | Theorems on stabilization for $ K _{i} $- | |
| − | + | functors under the transfer from the stable objects $ K _{i} (R) $ | |
| − | + | to unstable ones are also called stability theorems (see [[#References|[6]]]). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Theorems on stabilization for | ||
====References==== | ====References==== | ||
| Line 25: | Line 58: | ||
====Comments==== | ====Comments==== | ||
| − | Many groups in algebraic | + | Many groups in algebraic $ K $- |
| + | theory are defined as direct limits. For example, [[#References|[a1]]], $ K _{1} (R) = \mathop{\rm lim}\nolimits \ \mathop{\rm GL}\nolimits _{n} (R) / E _{n} (R) $ | ||
| + | for any associative ring $ R $ | ||
| + | with $ 1 $. | ||
| + | The corresponding stability theorem asserts that the sequence is eventually stable, i.e., the mappings become isomorphisms starting from some point. In the above example, $ K _{1} (R) = \mathop{\rm GL}\nolimits _{n} (R) / E _{n} (R) $ | ||
| + | for $ n \geq \mathop{\rm sr}\nolimits (R) +1 $, | ||
| + | where $ \mathop{\rm sr}\nolimits (R) $ | ||
| + | is the Bass stable rank of $ R $[[#References|[a1]]]–[[#References|[a3]]]. See [[#References|[a4]]] for a similar result for higher $ K $- | ||
| + | functors. For the $ K _{0} $- | ||
| + | functor, a stability result is the so-called cancellation theorem [[#References|[a1]]]. A similar result for modules with quadratic forms is known as the [[Witt theorem|Witt theorem]]. | ||
| − | The most common meaning of "stability theorem" is that given in the last sentence of the main article above (i.e. stabilization of | + | The most common meaning of "stability theorem" is that given in the last sentence of the main article above (i.e. stabilization of $ K _{i} $- |
| + | functors under transfer from stable to unstable objects), cf. [[#References|[a3]]]. | ||
| − | The stability theorem for Whitehead groups, or Bass–Heller–Swan theorem, was generalized to all | + | The stability theorem for Whitehead groups, or Bass–Heller–Swan theorem, was generalized to all $ K $- |
| + | groups by D. Quillen, [[#References|[a4]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Bass, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706054.png" />-theory and stable algebra" ''Publ. Math. IHES'' , '''22''' (1964) pp. 485–544 {{MR|0174604}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.N. Vaserstein, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706055.png" />-theory and the congruence subgroup problem" ''Math. Notes'' , '''5''' (1969) pp. 141–148 ''Mat. Zametki'' , '''5''' (1969) pp. 233–244 {{MR|246941}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Suslin, "Stability in algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706056.png" />-theory" R.K. Dennis (ed.) , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706057.png" />-theory (Oberwolfach, 1980)'' , ''Lect. notes in math.'' , '''966''' , Springer (1982) pp. 304–333 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D. Quillen, "Higher algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706058.png" />-theory I" H. Bass (ed.) , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706059.png" />-theory I (Battelle Inst. Conf.)'' , ''Lect. notes in math.'' , '''341''' , Springer (1973) pp. 85–147 {{MR|338129}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Bass, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706054.png" />-theory and stable algebra" ''Publ. Math. IHES'' , '''22''' (1964) pp. 485–544 {{MR|0174604}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.N. Vaserstein, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706055.png" />-theory and the congruence subgroup problem" ''Math. Notes'' , '''5''' (1969) pp. 141–148 ''Mat. Zametki'' , '''5''' (1969) pp. 233–244 {{MR|246941}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Suslin, "Stability in algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706056.png" />-theory" R.K. Dennis (ed.) , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706057.png" />-theory (Oberwolfach, 1980)'' , ''Lect. notes in math.'' , '''966''' , Springer (1982) pp. 304–333 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D. Quillen, "Higher algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706058.png" />-theory I" H. Bass (ed.) , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706059.png" />-theory I (Battelle Inst. Conf.)'' , ''Lect. notes in math.'' , '''341''' , Springer (1973) pp. 85–147 {{MR|338129}} {{ZBL|}} </TD></TR></table> | ||
Revision as of 17:26, 17 January 2020
Assertions on the invariance of the groups $ K _{i} (R) $
or their subgroups, given certain special extensions of the ground ring $ R $(
see Algebraic $ K $-
theory).
The following are the best-known stability theorems. Let $ R $ be a regular ring (cf. Regular ring (in commutative algebra)) and let $ R[t _{1} \dots t _{n} ] $ be the ring of polynomials in the variables $ t _{1} \dots t _{n} $ over $ R $. The stability theorem for Whitehead groups under the transfer from $ R $ to $ R[t _{1} \dots t _{n} ] $, [1], states that the natural homomorphism imbedding $ R $ in $ R[t _{1} \dots t _{n} ] $ induces an isomorphism between $ K _{1} (R) $ and $ K _{1} (R[t _{1} \dots t _{n} ]) $( cf. also Whitehead group).
In the case of a skew-field $ R $ that is finite-dimensional over its centre $ Z(R) $, one can define a reduced-norm homomorphism $ \mathop{\rm Nrd}\nolimits _{R} : \ R ^ \star \rightarrow Z(R) ^ \star $ of the multiplicative group $ R ^ \star $ of $ R $ into the multiplicative group $ Z(R) ^ \star $ of its centre. The kernel of this homomorphism, usually written as $ \mathop{\rm SL}\nolimits (1,\ R) $, determines the reduced Whitehead group $ SK _{1} (R) $ of $ R $: $$ SK _{1} (R) \simeq { \mathop{\rm SL}\nolimits (1,\ R)} / {[R ^ \star ,\ R ^ \star ]} $$( see Special linear group), which is a subgroup in $ K _{1} (R) $. If $ Z(R)(t _{1} \dots t _{n} ) $ is the field of rational functions in $ t _{1} \dots t _{n} $ over $ Z(R) $, then the algebra $$ R(t _{1} \dots t _{n} ) = R \otimes _{Z(R)} Z(R)(t _{1} \dots t _{n} ) $$ is a skew-field, and the natural imbedding $ \phi _ {t _{1} \dots t _ n} $ of $ R $ in $ R(t _{1} \dots t _{n} ) $ induces a homomorphism $$ \psi _ {t _{1} \dots t _ n} ^ \prime : \ SK _{1} (R) \rightarrow SK _{1} (R(t _{1} \dots t _{n} )). $$ The stability theorem for reduced Whitehead groups states that the homomorphism $ \psi _ {t _{1} \dots t _ n} ^ \prime $ is bijective ([2], see also [3]). Similar statements are also true in unitary and spinor algebraic $ K $- theories [4], [5].
Theorems on stabilization for $ K _{i} $- functors under the transfer from the stable objects $ K _{i} (R) $ to unstable ones are also called stability theorems (see [6]).
References
| [1] | H. Bass, A. Heller, R. Swan, "The Whitehead group of a polynomial extension" Publ. Math. IHES : 22 (1964) pp. 61–79 MR0174605 Zbl 0248.18026 |
| [2] | V.P. Platonov, "Reduced 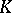 -theory and approximation in algebraic groups" Proc. Steklov Inst. Math. , 142 (1976) pp. 213–224 Trudy Mat. Inst. Steklov. , 142 (1976) pp. 198–207 MR568310 -theory and approximation in algebraic groups" Proc. Steklov Inst. Math. , 142 (1976) pp. 213–224 Trudy Mat. Inst. Steklov. , 142 (1976) pp. 198–207 MR568310 |
| [3] | V.P. Platonov, V.I. Yanchevskii, "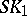 for division rings of noncommutative rational functions" Soviet Math. Dokl. , 20 : 6 (1976) pp. 1393–1397 Dokl. Akad. Nauk SSSR , 249 : 5 (1979) pp. 1064–1068 MR0553335 Zbl 0437.16015 for division rings of noncommutative rational functions" Soviet Math. Dokl. , 20 : 6 (1976) pp. 1393–1397 Dokl. Akad. Nauk SSSR , 249 : 5 (1979) pp. 1064–1068 MR0553335 Zbl 0437.16015 |
| [4] | V.I. Yanchevskii, "Reduced unitary 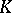 -theory. Applications to algebraic groups" Math. USSR Sb. , 38 (1981) pp. 533–548 Mat. Sb. , 110 : 4 (1979) pp. 579–596 MR1331389 MR0919253 MR0772116 MR0684770 MR0549289 MR0562210 MR0509375 MR0508832 -theory. Applications to algebraic groups" Math. USSR Sb. , 38 (1981) pp. 533–548 Mat. Sb. , 110 : 4 (1979) pp. 579–596 MR1331389 MR0919253 MR0772116 MR0684770 MR0549289 MR0562210 MR0509375 MR0508832 |
| [5] | A.P. Monastyrnyi, V.I. Yanchevskii, "Whitehead groups of spinor groups" Math. USSR Izv. , 54 : 1 (1991) pp. 61–100 Izv. Akad. Nauk SSSR Ser. Mat. , 54 : 1 (1990) pp. 60–96 MR1044048 |
| [6] | H. Bass, "Algebraic 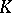 -theory" , Benjamin (1968) MR249491 -theory" , Benjamin (1968) MR249491 |
Comments
Many groups in algebraic $ K $- theory are defined as direct limits. For example, [a1], $ K _{1} (R) = \mathop{\rm lim}\nolimits \ \mathop{\rm GL}\nolimits _{n} (R) / E _{n} (R) $ for any associative ring $ R $ with $ 1 $. The corresponding stability theorem asserts that the sequence is eventually stable, i.e., the mappings become isomorphisms starting from some point. In the above example, $ K _{1} (R) = \mathop{\rm GL}\nolimits _{n} (R) / E _{n} (R) $ for $ n \geq \mathop{\rm sr}\nolimits (R) +1 $, where $ \mathop{\rm sr}\nolimits (R) $ is the Bass stable rank of $ R $[a1]–[a3]. See [a4] for a similar result for higher $ K $- functors. For the $ K _{0} $- functor, a stability result is the so-called cancellation theorem [a1]. A similar result for modules with quadratic forms is known as the Witt theorem.
The most common meaning of "stability theorem" is that given in the last sentence of the main article above (i.e. stabilization of $ K _{i} $- functors under transfer from stable to unstable objects), cf. [a3].
The stability theorem for Whitehead groups, or Bass–Heller–Swan theorem, was generalized to all $ K $- groups by D. Quillen, [a4].
References
| [a1] | H. Bass, "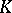 -theory and stable algebra" Publ. Math. IHES , 22 (1964) pp. 485–544 MR0174604 -theory and stable algebra" Publ. Math. IHES , 22 (1964) pp. 485–544 MR0174604 |
| [a2] | L.N. Vaserstein, "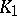 -theory and the congruence subgroup problem" Math. Notes , 5 (1969) pp. 141–148 Mat. Zametki , 5 (1969) pp. 233–244 MR246941 -theory and the congruence subgroup problem" Math. Notes , 5 (1969) pp. 141–148 Mat. Zametki , 5 (1969) pp. 233–244 MR246941 |
| [a3] | A. Suslin, "Stability in algebraic 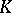 -theory" R.K. Dennis (ed.) , Algebraic -theory" R.K. Dennis (ed.) , Algebraic 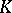 -theory (Oberwolfach, 1980) , Lect. notes in math. , 966 , Springer (1982) pp. 304–333 -theory (Oberwolfach, 1980) , Lect. notes in math. , 966 , Springer (1982) pp. 304–333 |
| [a4] | D. Quillen, "Higher algebraic  -theory I" H. Bass (ed.) , Algebraic -theory I" H. Bass (ed.) , Algebraic 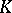 -theory I (Battelle Inst. Conf.) , Lect. notes in math. , 341 , Springer (1973) pp. 85–147 MR338129 -theory I (Battelle Inst. Conf.) , Lect. notes in math. , 341 , Springer (1973) pp. 85–147 MR338129 |
Stability theorems in algebraic K-theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stability_theorems_in_algebraic_K-theory&oldid=44336