Difference between revisions of "Inverse scattering, full-line case"
(Importing text file) |
m (fixed formatting) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|want}} | ||
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130050/i1300501.png" />, where the bar stands for complex conjugation. Consider the (direct) scattering problem: | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130050/i1300501.png" />, where the bar stands for complex conjugation. Consider the (direct) scattering problem: | ||
| Line 67: | Line 68: | ||
The inverse scattering problem (ISP) consists of finding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130050/i13005055.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130050/i13005056.png" />. | The inverse scattering problem (ISP) consists of finding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130050/i13005055.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130050/i13005056.png" />. | ||
| − | The inverse scattering problem has at most one solution in the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130050/i13005057.png" />. This solution can be calculated by the following Marchenko method: | + | The inverse scattering problem has at most one solution in the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130050/i13005057.png" />. This solution can be calculated by the following Marchenko method: |
| + | <table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">1</td> <td colname="2" style="background-color:white;" colspan="1">Define | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130050/i13005058.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a5)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130050/i13005058.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a5)</td></tr></table> | ||
Revision as of 05:32, 23 July 2018
Let 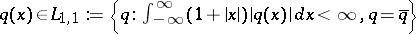 , where the bar stands for complex conjugation. Consider the (direct) scattering problem:
, where the bar stands for complex conjugation. Consider the (direct) scattering problem:
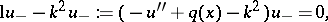 | (a1) |
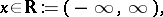 |
 | (a2) |
The coefficients  and
and  are called the reflection and transmission coefficients. One can prove that
are called the reflection and transmission coefficients. One can prove that 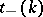 is analytic in
is analytic in 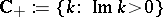 except at a finite number of points
except at a finite number of points 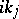 ,
, 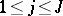 ,
, 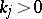 , which are simple poles of
, which are simple poles of 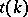 .
.
Problem (a1)–(a2) describes scattering by a plane wave 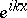 falling from
falling from 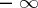 and scattered by the potential
and scattered by the potential 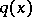 .
.
One can also consider the scattering of the plane wave falling from 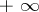 :
:
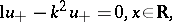 | (a3) |
 | (a4) |
One proves that 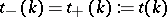 ,
, 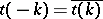 ,
, 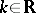 , where the bar stands for complex conjugation,
, where the bar stands for complex conjugation, 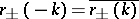 . The matrix
. The matrix
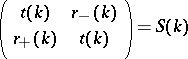 |
is called the 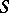 -matrix (cf. Scattering matrix). Conservation of energy implies
-matrix (cf. Scattering matrix). Conservation of energy implies  .
.
Let 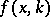 and
and 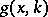 be the solutions to (a1) satisfying the conditions:
be the solutions to (a1) satisfying the conditions:
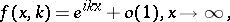 |
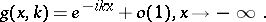 |
Then
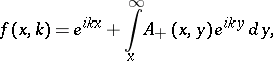 |
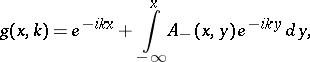 |
where 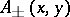 are the kernels which define the transformation operators. One has
are the kernels which define the transformation operators. One has
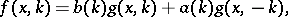 |
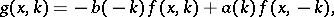 |
where
 |
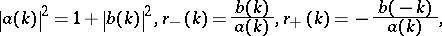 |
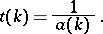 |
The function 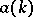 is analytic in
is analytic in 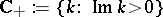 and has finitely many simple zeros all of which are at the points
and has finitely many simple zeros all of which are at the points 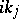 ,
, 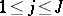 ,
, 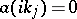 ,
, 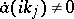 ,
, 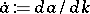 .
.
If 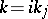 , then
, then 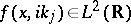 ,
,
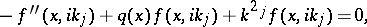 |
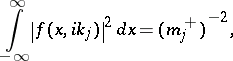 |
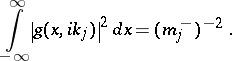 |
The numbers 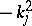 are the eigenvalues of the operator
are the eigenvalues of the operator  in
in 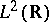 . They are called the bound states.
. They are called the bound states.
The scattering data are the values
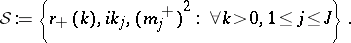 |
The inverse scattering problem (ISP) consists of finding 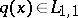 from
from 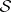 .
.
The inverse scattering problem has at most one solution in the class 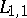 . This solution can be calculated by the following Marchenko method:
. This solution can be calculated by the following Marchenko method:
<tbody> </tbody>
|
The main result [a7] is the characterization property for the scattering data: In order that 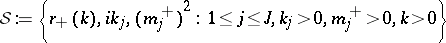 be the scattering data corresponding to a
be the scattering data corresponding to a 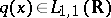 , it is necessary and sufficient that the following conditions hold:
, it is necessary and sufficient that the following conditions hold:
i) 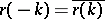 for
for 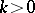 , the function
, the function 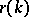 for
for 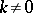 is continuous,
is continuous,
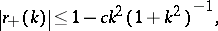 |
where 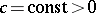 , and
, and  as
as 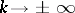 .
.
ii) The function
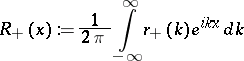 |
is absolutely continuous and
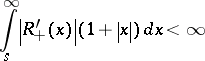 |
for every 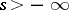 .
.
iii) Denote
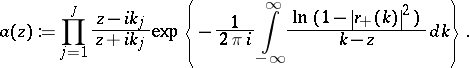 |
The function 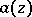 is continuous in
is continuous in 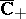 and
and
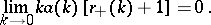 |
iv) The function
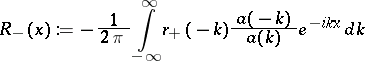 |
is absolutely continuous and
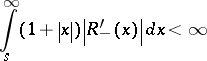 |
for every 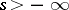 .
.
A similar result holds for the data
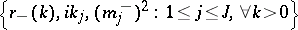 |
and the potential 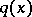 can be obtained by the Marchenko method,
can be obtained by the Marchenko method, 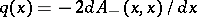 .
.
In [a2] the above theory is generalized to the case when 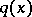 tends to a different constants as
tends to a different constants as 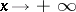 and
and 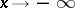 .
.
In [a5] a different approach to solving the inverse scattering problem is described for
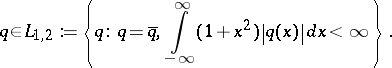 |
The approach in [a5] is based on a trace formula.
If 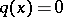 for
for  , then the reflection coefficient
, then the reflection coefficient 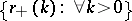 alone, without the knowledge of
alone, without the knowledge of 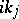 and
and 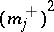 , determines
, determines 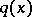 uniquely. A simple proof of this and similar statements, based on property
uniquely. A simple proof of this and similar statements, based on property 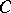 for ordinary differential equations (cf. Ordinary differential equations, property
for ordinary differential equations (cf. Ordinary differential equations, property 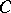 for), is given in [a10].
for), is given in [a10].
An inverse scattering problem for an inhomogeneous Schrödinger equation is studied in [a5].
The inverse scattering method is a tool for solving many evolution equations (cf. also Evolution equation) and is used in, e.g., soliton theory [a7], [a1], [a3], [a6] (cf. also Korteweg–de Vries equation; Harry Dym equation).
Methods for adding and removing bound states are described in [a5]. They are based on the Darboux–Crum transformations and commutation formulas.
A large bibliography can be found in [a4].
References
| [a1] | M. Ablowitz, H. Segur, "Solutions and inverse scattering transform" , SIAM (1981) |
| [a2] | A. Cohen, T. Kappeler, "Scattering and inverse scattering for step-like potentials in the Schrödinger equation" Indiana Math. J. , 34 (1985) pp. 127–180 |
| [a3] | F. Calogero, A. Degasperis, "Solutions and the spectral transform" , North-Holland (1982) |
| [a4] | K. Chadan, P. Sabatier, "Inverse problems in quantum scattering" , Springer (1989) |
| [a5] | P. Deift, E. Trubowitz, "Inverse scattering on the line" Commun. Pure Appl. Math. , 32 (1979) pp. 121–251 |
| [a6] | L. Faddeev, L. Takhtadjian, "Hamiltonian methods in the theory of solutions" , Springer (1986) |
| [a7] | V. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) |
| [a8] | A.G. Ramm, "Multidimensional inverse scattering problems" , Longman/Wiley (1992) |
| [a9] | A.G. Ramm, "Inverse problem for an inhomogeneous Schrödinger equation" J. Math. Phys. , 40 : 8 (1999) pp. 3876–3880 |
| [a10] | A.G. Ramm, "Property C for ODE and applications to inverse problems" A.G. Ramm (ed.) P.N. Shivakumar (ed.) A.V. Strauss (ed.) , Operator Theory and Applications , Fields Inst. Commun. , 25 , Amer. Math. Soc. (2000) pp. 15–75 |
Inverse scattering, full-line case. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inverse_scattering,_full-line_case&oldid=43394
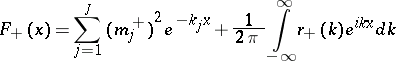
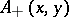 :
:
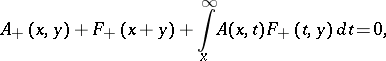
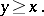
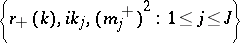 correspond to a
correspond to a 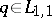 , then equation (a5) is uniquely solvable in
, then equation (a5) is uniquely solvable in 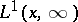 for every
for every 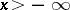 .
.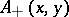 is found, then
is found, then 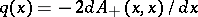 .
.