Difference between revisions of "Baer multiplication"
From Encyclopedia of Mathematics
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | A binary operation on the set of classes of extensions of modules, proposed by R. Baer [[#References|[1]]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150201.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150202.png" /> be arbitrary modules. An extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150203.png" /> with kernel <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150204.png" /> is an [[ | + | A binary operation on the set of classes of [[Extension of a module|extensions of modules]], proposed by R. Baer [[#References|[1]]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150201.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150202.png" /> be arbitrary modules. An extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150203.png" /> with kernel <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150204.png" /> is an [[exact sequence]]: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150205.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150205.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | ||
| − | The extension (1) is called equivalent to the extension | + | The extension (1) is called ''equivalent'' to the extension |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150206.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015020/b0150206.png" /></td> </tr></table> | ||
| Line 38: | Line 38: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Baer, "Erweiterung von Gruppen und ihren Isomorphismen" ''Math. Z.'' , '''38''' (1934) pp. 374–416</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> R. Baer, "Erweiterung von Gruppen und ihren Isomorphismen" ''Math. Z.'' , '''38''' (1934) pp. 374–416</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)</TD></TR> | ||
| + | </table> | ||
Revision as of 08:51, 11 April 2018
A binary operation on the set of classes of extensions of modules, proposed by R. Baer [1]. Let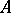 
and 
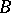be arbitrary modules. An extension of 
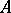with kernel 
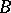is an exact sequence:
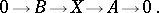 | (1) |
The extension (1) is called equivalent to the extension
 |
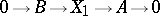if there exists a homomorphism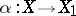 
forming part of the commutative diagram
 |
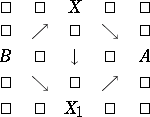The set of equivalence classes of extensions is denoted by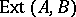 
. The Baer multiplication on 
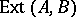is induced by the operation of products of extensions defined as follows. Let
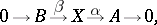 | (2) |
 | (3) |
be two extensions. In the direct sum 
the submodules
 |
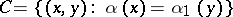and
 |
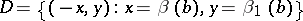are selected. Clearly,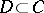 
, so that one can define the quotient module 
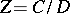. The Baer product of the extensions (2) and (3) is the extension
 |
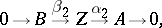where
 |
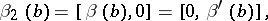and
 |
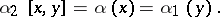References
| [1] | R. Baer, "Erweiterung von Gruppen und ihren Isomorphismen" Math. Z. , 38 (1934) pp. 374–416 |
| [2] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
How to Cite This Entry:
Baer multiplication. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baer_multiplication&oldid=43113
Baer multiplication. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baer_multiplication&oldid=43113
This article was adapted from an original article by V.E. Govorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article