Difference between revisions of "Weak P-point"
(Importing text file) |
|||
| Line 1: | Line 1: | ||
| − | A point in a [[Topological space|topological space]] that is not an [[Accumulation point|accumulation point]] of any countable subset of the space. Every [[P-point|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300302.png" />-point]] is a weak <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300303.png" />-point. Weak <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300304.png" />-points were introduced by K. Kunen [[#References|[a2]]] in his proof that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300305.png" />, the remainder <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300306.png" /> of the [[Stone–Čech compactification|Stone–Čech compactification]] of the natural numbers, is not homogeneous. In fact, Kunen proved that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300307.png" /> contains points that are very much like <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300308.png" />-points, so-called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300309.png" />-OK points: A point is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003011.png" />-OK if for every sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003012.png" /> of neighbourhoods there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003013.png" />-sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003014.png" /> of neighbourhoods such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003015.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003016.png" /> has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003017.png" /> elements. A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003018.png" />-OK point cannot be an accumulation point of any set that satisfies the countable chain condition (cf. [[Chain condition|Chain condition]]), hence it is not an accumulation point of any countable set either. | + | A point in a [[Topological space|topological space]] that is not an [[Accumulation point|accumulation point]] of any countable subset of the space. Every [[P-point|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300302.png" />-point]] is a weak <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300303.png" />-point. Weak <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300304.png" />-points were introduced by K. Kunen [[#References|[a2]]] in his proof that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300305.png" />, the remainder <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300306.png" /> of the [[Stone–Čech compactification|Stone–Čech compactification]] of the natural numbers, is not homogeneous (cf. [[Cech-Stone compactification of omega]]). In fact, Kunen proved that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300307.png" /> contains points that are very much like <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300308.png" />-points, so-called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w1300309.png" />-OK points: A point is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003011.png" />-OK if for every sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003012.png" /> of neighbourhoods there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003013.png" />-sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003014.png" /> of neighbourhoods such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003015.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003016.png" /> has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003017.png" /> elements. A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003018.png" />-OK point cannot be an accumulation point of any set that satisfies the countable chain condition (cf. [[Chain condition|Chain condition]]), hence it is not an accumulation point of any countable set either. |
Weak <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003019.png" />-points and similar types of points have been used to give so-called "effective" proofs that many spaces are not homogeneous [[#References|[a3]]], [[#References|[a4]]]. These proofs are generally considered simpler than the proof by Z. Frolík [[#References|[a1]]] of the non-homogeneity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003020.png" />, which takes a countably infinite discrete subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003021.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003022.png" /> (whose closure is homeomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003023.png" />) and shows that a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003024.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003025.png" /> cannot be mapped by any auto-homeomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003026.png" /> to its copy in the closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003027.png" />. "Simpler" does not necessarily mean that the proof is easier, but that the properties used to distinguish the point are of a simpler nature. | Weak <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003019.png" />-points and similar types of points have been used to give so-called "effective" proofs that many spaces are not homogeneous [[#References|[a3]]], [[#References|[a4]]]. These proofs are generally considered simpler than the proof by Z. Frolík [[#References|[a1]]] of the non-homogeneity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003020.png" />, which takes a countably infinite discrete subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003021.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003022.png" /> (whose closure is homeomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003023.png" />) and shows that a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003024.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003025.png" /> cannot be mapped by any auto-homeomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003026.png" /> to its copy in the closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130030/w13003027.png" />. "Simpler" does not necessarily mean that the proof is easier, but that the properties used to distinguish the point are of a simpler nature. | ||
Revision as of 21:29, 19 November 2017
A point in a topological space that is not an accumulation point of any countable subset of the space. Every 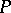 -point is a weak
-point is a weak 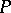 -point. Weak
-point. Weak 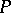 -points were introduced by K. Kunen [a2] in his proof that
-points were introduced by K. Kunen [a2] in his proof that 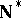 , the remainder
, the remainder 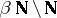 of the Stone–Čech compactification of the natural numbers, is not homogeneous (cf. Cech-Stone compactification of omega). In fact, Kunen proved that
of the Stone–Čech compactification of the natural numbers, is not homogeneous (cf. Cech-Stone compactification of omega). In fact, Kunen proved that 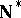 contains points that are very much like
contains points that are very much like 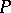 -points, so-called
-points, so-called  -OK points: A point is
-OK points: A point is  -OK if for every sequence
-OK if for every sequence 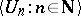 of neighbourhoods there is a
of neighbourhoods there is a  -sequence
-sequence 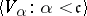 of neighbourhoods such that
of neighbourhoods such that 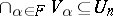 whenever
whenever  has
has  elements. A
elements. A  -OK point cannot be an accumulation point of any set that satisfies the countable chain condition (cf. Chain condition), hence it is not an accumulation point of any countable set either.
-OK point cannot be an accumulation point of any set that satisfies the countable chain condition (cf. Chain condition), hence it is not an accumulation point of any countable set either.
Weak 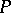 -points and similar types of points have been used to give so-called "effective" proofs that many spaces are not homogeneous [a3], [a4]. These proofs are generally considered simpler than the proof by Z. Frolík [a1] of the non-homogeneity of
-points and similar types of points have been used to give so-called "effective" proofs that many spaces are not homogeneous [a3], [a4]. These proofs are generally considered simpler than the proof by Z. Frolík [a1] of the non-homogeneity of 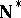 , which takes a countably infinite discrete subset
, which takes a countably infinite discrete subset 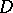 of
of 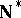 (whose closure is homeomorphic to
(whose closure is homeomorphic to 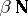 ) and shows that a point
) and shows that a point 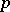 of
of 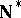 cannot be mapped by any auto-homeomorphism of
cannot be mapped by any auto-homeomorphism of 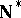 to its copy in the closure of
to its copy in the closure of 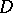 . "Simpler" does not necessarily mean that the proof is easier, but that the properties used to distinguish the point are of a simpler nature.
. "Simpler" does not necessarily mean that the proof is easier, but that the properties used to distinguish the point are of a simpler nature.
References
| [a1] | Z. Frolík, "Non-homogeneity of 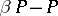 " Comment. Math. Univ. Carolinae , 8 (1967) pp. 705–709 " Comment. Math. Univ. Carolinae , 8 (1967) pp. 705–709 |
| [a2] | K. Kunen, "Weak 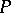 -points in -points in 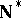 " Á. Császár (ed.) , Topology (Proc. Fourth Colloq., Budapest, 1978) , II , North-Holland (1980) pp. 741–749 " Á. Császár (ed.) , Topology (Proc. Fourth Colloq., Budapest, 1978) , II , North-Holland (1980) pp. 741–749 |
| [a3] | J. van Mill, "Weak 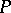 -points in Čech–Stone compactifications" Trans. Amer. Math. Soc. , 273 (1982) pp. 657–678 -points in Čech–Stone compactifications" Trans. Amer. Math. Soc. , 273 (1982) pp. 657–678 |
| [a4] | J. van Mill, "Sixteen topological types in 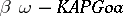 " Topol. Appl. , 13 : 1 (1982) pp. 43–57 " Topol. Appl. , 13 : 1 (1982) pp. 43–57 |
Weak P-point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weak_P-point&oldid=42348