Difference between revisions of "Allison-Hein triple system"
Ulf Rehmann (talk | contribs) m (moved Allison–Hein triple system to Allison-Hein triple system: ascii title) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | The concept of a triple system, i.e. a [[Vector space|vector space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302001.png" /> over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302002.png" /> together with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302003.png" />-trilinear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302004.png" />, is mainly used in the theory of non-associative algebras and appears in the construction of Lie algebras (cf. also [[Lie algebra|Lie algebra]]; [[Non-associative rings and algebras|Non-associative rings and algebras]]). | + | The concept of a triple system, i.e. a [[Vector space|vector space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302001.png" /> over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302002.png" /> together with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302003.png" />-[[trilinear mapping]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302004.png" />, is mainly used in the theory of non-associative algebras and appears in the construction of Lie algebras (cf. also [[Lie algebra|Lie algebra]]; [[Non-associative rings and algebras|Non-associative rings and algebras]]). |
A [[Module|module]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302005.png" /> over a field of characteristic not equal to two or three together with a trilinear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302006.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302007.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302008.png" /> is said to be an Allison–Hein triple system (or a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a13020010.png" />-ternary algebra) if | A [[Module|module]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302005.png" /> over a field of characteristic not equal to two or three together with a trilinear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302006.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302007.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a1302008.png" /> is said to be an Allison–Hein triple system (or a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a13020010.png" />-ternary algebra) if | ||
Revision as of 20:33, 19 September 2017
The concept of a triple system, i.e. a vector space  over a field
over a field  together with a
together with a  -trilinear mapping
-trilinear mapping  , is mainly used in the theory of non-associative algebras and appears in the construction of Lie algebras (cf. also Lie algebra; Non-associative rings and algebras).
, is mainly used in the theory of non-associative algebras and appears in the construction of Lie algebras (cf. also Lie algebra; Non-associative rings and algebras).
A module  over a field of characteristic not equal to two or three together with a trilinear mapping
over a field of characteristic not equal to two or three together with a trilinear mapping  from
from  to
to  is said to be an Allison–Hein triple system (or a
is said to be an Allison–Hein triple system (or a 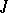 -ternary algebra) if
-ternary algebra) if
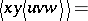 | (a1) |
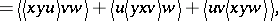 |
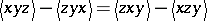 | (a2) |
for all 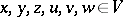 .
.
From the identities (a1) and (a2) one deduces the relation
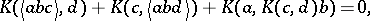 |
where 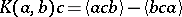 . Hence this triple system may be regarded as a variation of a Freudenthal–Kantor triple system. In particular, it is important that the linear span
. Hence this triple system may be regarded as a variation of a Freudenthal–Kantor triple system. In particular, it is important that the linear span  of the set
of the set 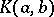 is a Jordan subalgebra (cf. also Jordan algebra) of
is a Jordan subalgebra (cf. also Jordan algebra) of 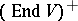 with respect to
with respect to 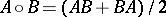 .
.
References
| [a1] | B.N. Allison, "A construction of Lie algebras from 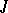 -ternary algebras" Amer. J. Math. , 98 (1976) pp. 285–294 -ternary algebras" Amer. J. Math. , 98 (1976) pp. 285–294 |
| [a2] | W. Hein, "A construction of Lie algebras by triple systems" Trans. Amer. Math. Soc. , 205 (1975) pp. 79–95 |
| [a3] | N. Kamiya, "A structure theory of Freudenthal–Kantor triple systems II" Commun. Math. Univ. Sancti Pauli , 38 (1989) pp. 41–60 |
| [a4] | K. Yamaguti, "On the metasymplectic geometry and triple systems" Surikaisekikenkyusho Kokyuroku, Res. Inst. Math. Sci. Kyoto Univ. , 306 (1977) pp. 55–92 (In Japanese) |
Allison-Hein triple system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Allison-Hein_triple_system&oldid=41899