Symmetric algebra

A generalization of a polynomial algebra. If 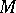is a unital module over a commutative associative ring 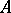with an identity, then the symmetric algebra of 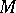is the algebra 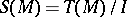, where 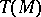is the tensor algebra of 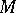and 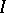is the ideal generated by the elements of the form 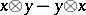(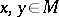). A symmetric algebra is a commutative associative 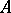-algebra with an identity. It is graded:

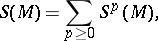where 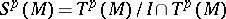, and 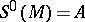, 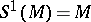. The module 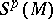is called the 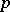-th symmetric power of the module 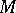. If 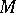is a free module with finite basis , then the correspondence 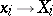(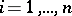) extends to an isomorphism of 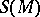onto the polynomial algebra 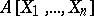(see Ring of polynomials).

For any homomorphism 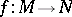of 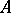-modules, the 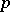-th tensor power 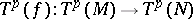induces a homomorphism 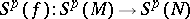(the -th 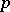symmetric power of the homomorphism 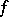). A homomorphism 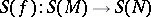of 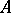-algebras is obtained. The correspondences 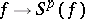and 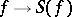are, respectively, covariant functors from the category of 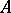-modules into itself and into the category of 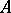-algebras. For any two 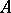-modules 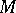and 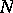there is a natural isomorphism .

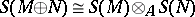If 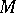is a vector space over a field of characteristic 0, then the symmetrization 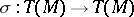(cf. Symmetrization (of tensors)) defines an isomorphism from the symmetric algebra 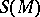onto the algebra 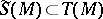of symmetric contravariant tensors over 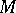relative to symmetric multiplication:

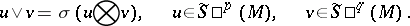References

[1]	N. Bourbaki, "Eléments de mathématique" , 2. Algèbre , Hermann (1964) pp. Chapt. IV-VI
[2]	A.I. Kostrikin, Yu.I. Manin, "Linear algebra and geometry" , Gordon & Breach (1989) (Translated from Russian)

Comments

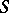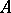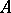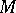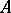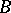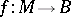The functor from -modules to commutative unitary -algebras solves the following universal problem. Let be an -module and a commutative unitary -algebra. For each homomorphism of 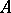-modules there is a unique homomorphism 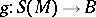of 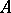-algebras such that 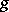restricted to 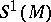coincides with 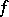. Thus, 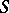is a left-adjoint functor of the underlying functor from the category of commutative unitary 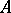-algebras to the category of 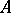-modules.