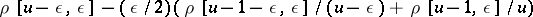Difference between revisions of "Dickman function"
(Importing text file) |
m (better) |
||
| Line 33: | Line 33: | ||
d) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009060.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009061.png" />. | d) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009060.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009061.png" />. | ||
| − | The Dickman function is one of a parameterized family of related functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009062.png" />, [[#References|[a12]]], and a wider class of similar delay-differential equations has been studied in [[#References|[a7]]]. A quick and simple bit of Mathematica code suffices to calculate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009063.png" /> to reasonable accuracy in the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009064.png" /> using step-size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009065.png" />. This code calculates a table of values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009066.png" /> at intervals of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009067.png" />, working back recursively into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009068.png" />: | + | The Dickman function is one of a parameterized family of related functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009062.png" />, [[#References|[a12]]], and a wider class of similar delay-differential equations has been studied in [[#References|[a7]]]. A quick and simple bit of Mathematica code suffices to calculate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009063.png" /> to reasonable accuracy in the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009064.png" /> using step-size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009065.png" />. This code calculates a table of values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009066.png" /> at intervals of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009067.png" />, working back recursively into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009068.png" />: |
| + | |||
| + | <table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009069.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009070.png" />,</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009071.png" />;</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009072.png" />;</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009073.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130090/d13009074.png" /></td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
Revision as of 21:49, 13 December 2016
The function 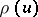 defined on
defined on  by the initial condition
by the initial condition 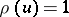 for
for 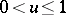 and by the delay-differential equation
and by the delay-differential equation 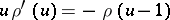 for
for 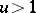 . Interest attaches to this function because of its connection to "smooth" numbers, i.e. numbers that are the product of many small prime numbers. Let
. Interest attaches to this function because of its connection to "smooth" numbers, i.e. numbers that are the product of many small prime numbers. Let  denote the number of positive integers less than or equal to
denote the number of positive integers less than or equal to  and free of prime divisors greater than
and free of prime divisors greater than 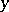 . When
. When  is much larger than
is much larger than 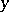 , it is a simple matter of inclusion-and-exclusion counting (cf. also Inclusion-exclusion formula) to show that
, it is a simple matter of inclusion-and-exclusion counting (cf. also Inclusion-exclusion formula) to show that 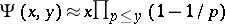 , where
, where 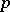 denotes a prime number. But the error terms grow rapidly, and the "main" term gives the wrong answer in the ranges of greatest interest, including the case when
denotes a prime number. But the error terms grow rapidly, and the "main" term gives the wrong answer in the ranges of greatest interest, including the case when 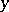 is comparable to a fixed fractional power of
is comparable to a fixed fractional power of  . For this case, K. Dickman found that
. For this case, K. Dickman found that 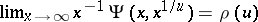 . If, in place of the restriction
. If, in place of the restriction 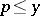 for
for 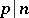 one takes the condition
one takes the condition 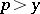 , the resulting
, the resulting 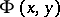 is approximated by
is approximated by 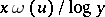 , where
, where 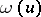 is the Bukhstab function, defined by
is the Bukhstab function, defined by 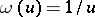 ,
,  , and
, and 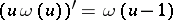 ,
, 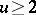 , where for
, where for 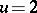 the right-hand derivative has to be taken, [a1]. Unlike
the right-hand derivative has to be taken, [a1]. Unlike 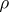 ,
, 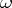 oscillates and tends to a positive limit, equal to
oscillates and tends to a positive limit, equal to 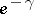 .
.
There are two combinatorial identities linking the Dickman function to 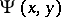 . Early work is based on the Bukhstab identity: With
. Early work is based on the Bukhstab identity: With 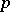 denoting a prime number, for
denoting a prime number, for 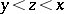 ,
,
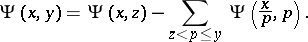 |
The usual heuristic device of replacing a sum over prime numbers by an integral with "prime density" 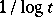 and replacing
and replacing 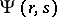 with
with 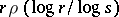 leads to an identity which, when
leads to an identity which, when 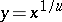 and
and 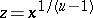 , simplifies to an integral equivalent to the definition of
, simplifies to an integral equivalent to the definition of 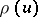 . N.G. de Bruijn carried this idea to its limits in [a2], but accuracy suffers when large and comparable estimated quantities must be subtracted. The more recent Hildebrand identity involves only additions and has the further advantage that the second input is the same
. N.G. de Bruijn carried this idea to its limits in [a2], but accuracy suffers when large and comparable estimated quantities must be subtracted. The more recent Hildebrand identity involves only additions and has the further advantage that the second input is the same 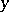 throughout:
throughout:
 |
Applications require estimates uniform in  ; the best known estimate along these lines, due to A. Hildebrand and based on the identity above, is
; the best known estimate along these lines, due to A. Hildebrand and based on the identity above, is
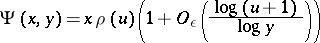 |
uniformly in 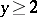 and
and 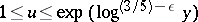 . There are similar results for algebraic integers, [a3].
. There are similar results for algebraic integers, [a3].
There are also results concerning the number of smooth integers in an interval, and concerning the distribution of smooth integers into congruence classes [a4], [a5].
The Riemann hypothesis (cf. Riemann hypotheses) implies 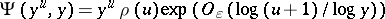 [a8].
[a8].
The analytical properties of 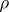 are reasonably well understood; calculus, analysis of the Laplace transform, and the saddle-point method are the key tools. The first extensive analysis is due to De Bruijn, and the function
are reasonably well understood; calculus, analysis of the Laplace transform, and the saddle-point method are the key tools. The first extensive analysis is due to De Bruijn, and the function 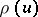 is sometimes termed the Dickman–De Bruijn function. One has [a10]:
is sometimes termed the Dickman–De Bruijn function. One has [a10]:
a) 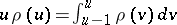 for
for 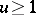 (so that
(so that 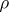 is positive for all positive
is positive for all positive  , and hence, from the definition, decreasing);
, and hence, from the definition, decreasing);
b) 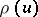 is log-concave, that is,
is log-concave, that is, 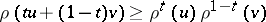 for
for 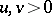 and
and 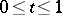 (K. Alladi);
(K. Alladi);
c) The Laplace transform
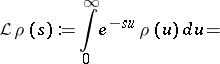 |
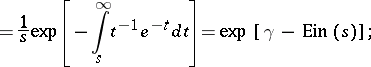 |
d) 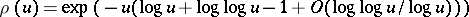 as
as 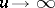 .
.
The Dickman function is one of a parameterized family of related functions 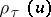 , [a12], and a wider class of similar delay-differential equations has been studied in [a7]. A quick and simple bit of Mathematica code suffices to calculate
, [a12], and a wider class of similar delay-differential equations has been studied in [a7]. A quick and simple bit of Mathematica code suffices to calculate 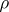 to reasonable accuracy in the interval
to reasonable accuracy in the interval 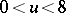 using step-size
using step-size 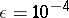 . This code calculates a table of values of
. This code calculates a table of values of 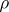 at intervals of length
at intervals of length  , working back recursively into
, working back recursively into 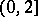 :
:
<tbody> </tbody>
|
References
| [a1] | N.G. de Bruijn, "On the number of positive integers 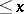 and free prime factors and free prime factors 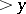 . II" Indag. Math. , 28 (1966) pp. 239–247 Nederl. Akad. Wetensch. Proc. Ser. A , 69 (1966) . II" Indag. Math. , 28 (1966) pp. 239–247 Nederl. Akad. Wetensch. Proc. Ser. A , 69 (1966) |
| [a2] | N.G. de Bruijn, "On the number of uncancelled elements in the sieve of Eratosthenes" Indag. Math. , 12 (1950) pp. 247–256 Nederl. Akad. Wetensch. Proc. , 53 (1950) pp. 803–812 |
| [a3] | J. Friedlander, "On the number of ideals free from large prime divisors" J. Reine Angew. Math. , 255 (1972) pp. 1–7 |
| [a4] | J. Friedlander, A. Granville, "Integers without large prime factors, in short intervals" Philos. Trans. Royal Soc. , 345 (1993) pp. 339–348 |
| [a5] | A. Granville, "On integers, without large prime factors, in arithmetic progressions II" Philos. Trans. Royal Soc. , 345 (1993) pp. 349–362 |
| [a6] | A. Hildebrand, G. Tenenbaum, "Integers without large prime factors" J. Théor. Nombres Bordeaux , 5 : 2 (1993) pp. 411–484 |
| [a7] | A. Hildebrand, G. Tenenbaum, "On a class of differential-difference equations arising in number theory" J. Anal. Math. , 61 (1993) pp. 145–179 |
| [a8] | A. Hildebrand, "Integers free of large prime factors and the Riemann hypothesis" Mathematika , 31 : 2 (1985) pp. 258–271 |
| [a9] | S. Hunter, J. Sorenson, "Approximating the number of integers free of large prime factors" Math. Comput. , 66 : 220 (1997) pp. 1729–1741 |
| [a10] | P. Moree, "Psixyology and Diophantine equations" Diss. Univ. Leiden (1993) |
| [a11] | E. Saias, "Sur le nombre des entiers sans grand facteur premier" J. Number Theory , 32 : 1 (1989) pp. 78–99 |
| [a12] | F.S. Wheeler, "Two differential-difference equations arising in number theory" Trans. Amer. Math. Soc. , 318 : 2 (1990) pp. 491–523 |
| [a13] | D.S. Mitrinović, J. Sandor, B. Crstici, "Handbook of number theory" , Kluwer Acad. Publ. (1996) pp. Sect. IV.21 |
| [a14] | K. Dickman, "On the frequency of numbers containing prime factors of a certain relative magnitude" Ark. Mat., Astron. och Fysik , 22A : 10 (1930) pp. 1–14 |
Dickman function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dickman_function&oldid=39999
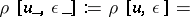
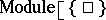 ,
,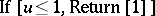 ;
;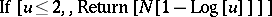 ;
;