Difference between revisions of "Witt ring"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (links) |
||
| Line 25: | Line 25: | ||
Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808044.png" /> is the residue class of the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808045.png" /> with respect to the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808046.png" />. | Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808044.png" /> is the residue class of the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808045.png" /> with respect to the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808046.png" />. | ||
| − | The Witt ring can often be calculated explicitly. Thus, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808047.png" /> is a quadratically (in particular, algebraically) closed field, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808048.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808049.png" /> is a real closed field, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808050.png" /> (the isomorphism is realized by sending the type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808051.png" /> to the signature of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808052.png" />); if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808053.png" /> is a Pythagorean field (i.e. the sum of two squares in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808054.png" /> is a square) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808055.png" /> is not real, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808056.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808057.png" /> is a finite field, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808058.png" /> is isomorphic to either the residue ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808059.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808060.png" />, depending on whether <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808061.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808062.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808063.png" />, respectively, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808064.png" /> is the number of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808065.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808066.png" /> is a complete local field and its class field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808067.png" /> has characteristic different from 2, then | + | The Witt ring can often be calculated explicitly. Thus, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808047.png" /> is a quadratically (in particular, algebraically) closed field, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808048.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808049.png" /> is a real closed field, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808050.png" /> (the isomorphism is realized by sending the type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808051.png" /> to the signature of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808052.png" />); if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808053.png" /> is a [[Pythagorean field]] (i.e. the sum of two squares in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808054.png" /> is a square) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808055.png" /> is not real, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808056.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808057.png" /> is a finite field, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808058.png" /> is isomorphic to either the residue ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808059.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808060.png" />, depending on whether <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808061.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808062.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808063.png" />, respectively, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808064.png" /> is the number of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808065.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808066.png" /> is a complete local field and its class field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808067.png" /> has characteristic different from 2, then |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808068.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808068.png" /></td> </tr></table> | ||
| Line 37: | Line 37: | ||
1) For any field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808078.png" /> the torsion subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808079.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808080.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808081.png" />-primary; | 1) For any field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808078.png" /> the torsion subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808079.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808080.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808081.png" />-primary; | ||
| − | 2) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808082.png" /> is a real field and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808083.png" /> is its Pythagorean closure (i.e. the smallest Pythagorean field containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808084.png" />), the sequence | + | 2) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808082.png" /> is a real field and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808083.png" /> is its [[Pythagorean closure]] (i.e. the smallest Pythagorean field containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808084.png" />), the sequence |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808085.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098080/w09808085.png" /></td> </tr></table> | ||
Revision as of 20:26, 10 December 2016
of a field 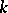 , ring of types of quadratic forms over
, ring of types of quadratic forms over 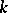
The ring 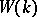 of classes of non-degenerate quadratic forms on finite-dimensional vector spaces over
of classes of non-degenerate quadratic forms on finite-dimensional vector spaces over 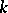 with the following equivalence relation: The form
with the following equivalence relation: The form 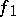 is equivalent to the form
is equivalent to the form 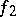 (
(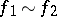 ) if and only if the orthogonal direct sum of the forms
) if and only if the orthogonal direct sum of the forms 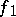 and
and 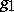 is isometric to the orthogonal direct sum of
is isometric to the orthogonal direct sum of 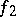 and
and 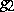 for certain neutral quadratic forms
for certain neutral quadratic forms 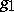 and
and 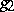 (cf. also Witt decomposition; Quadratic form). The operations of addition and multiplication in
(cf. also Witt decomposition; Quadratic form). The operations of addition and multiplication in 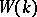 are induced by taking the orthogonal direct sum and the tensor product of forms.
are induced by taking the orthogonal direct sum and the tensor product of forms.
Let the characteristic of 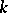 be different from 2. The definition of equivalence of forms is then equivalent to the following:
be different from 2. The definition of equivalence of forms is then equivalent to the following: 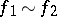 if and only if the anisotropic forms
if and only if the anisotropic forms 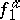 and
and 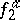 which correspond to
which correspond to 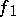 and
and 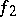 (cf. Witt decomposition) are isometric. The equivalence class of the form
(cf. Witt decomposition) are isometric. The equivalence class of the form 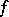 is said to be its type and is denoted by
is said to be its type and is denoted by 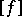 . The Witt ring, or the ring of types of quadratic forms, is an associative, commutative ring with a unit element. The unit element of
. The Witt ring, or the ring of types of quadratic forms, is an associative, commutative ring with a unit element. The unit element of 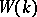 is the type of the form . (Here
is the type of the form . (Here 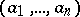 denotes the quadratic form
denotes the quadratic form 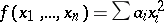 .) The type of the zero form of zero rank, containing also all the neutral forms, serves as the zero. The type
.) The type of the zero form of zero rank, containing also all the neutral forms, serves as the zero. The type 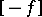 is opposite to the type
is opposite to the type 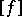 .
.
The additive group of the ring 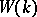 is said to be the Witt group of the field
is said to be the Witt group of the field 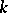 or the group of types of quadratic forms over
or the group of types of quadratic forms over 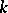 . The types of quadratic forms of the form
. The types of quadratic forms of the form 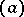 , where
, where  is an element of the multiplicative group
is an element of the multiplicative group 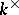 of
of 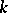 , generate the ring
, generate the ring 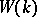 .
. 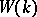 is completely determined by the following relations for the generators:
is completely determined by the following relations for the generators:
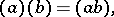 |
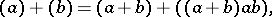 |
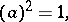 |
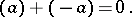 |
The Witt ring may be described as the ring isomorphic to the quotient ring of the integer group ring
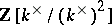 |
of the group 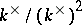 over the ideal generated by the elements
over the ideal generated by the elements
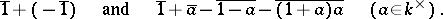 |
Here 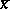 is the residue class of the element
is the residue class of the element  with respect to the subgroup
with respect to the subgroup 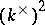 .
.
The Witt ring can often be calculated explicitly. Thus, if 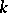 is a quadratically (in particular, algebraically) closed field, then
is a quadratically (in particular, algebraically) closed field, then 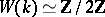 ; if
; if 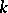 is a real closed field,
is a real closed field, 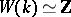 (the isomorphism is realized by sending the type
(the isomorphism is realized by sending the type 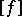 to the signature of the form
to the signature of the form 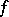 ); if
); if 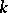 is a Pythagorean field (i.e. the sum of two squares in
is a Pythagorean field (i.e. the sum of two squares in 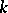 is a square) and
is a square) and 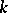 is not real, then
is not real, then 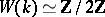 ; if
; if 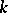 is a finite field,
is a finite field, 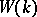 is isomorphic to either the residue ring
is isomorphic to either the residue ring 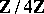 or
or 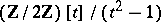 , depending on whether
, depending on whether 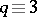 or
or 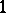
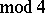 , respectively, where
, respectively, where 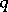 is the number of elements of
is the number of elements of 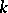 ; if
; if 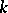 is a complete local field and its class field
is a complete local field and its class field 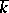 has characteristic different from 2, then
has characteristic different from 2, then
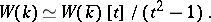 |
An extension 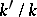 of
of 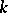 defines a homomorphism of Witt rings
defines a homomorphism of Witt rings 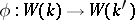 for which
for which 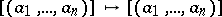 . If the extension is finite and is of odd degree,
. If the extension is finite and is of odd degree, 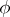 is a monomorphism and if, in addition, it is a Galois extension with group
is a monomorphism and if, in addition, it is a Galois extension with group 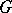 , the action of
, the action of 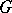 can be extended to
can be extended to 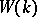 and
and
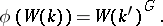 |
The general properties of a Witt ring may be described by Pfister's theorem:
1) For any field 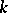 the torsion subgroup
the torsion subgroup 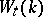 of
of 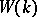 is
is  -primary;
-primary;
2) If 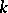 is a real field and
is a real field and 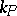 is its Pythagorean closure (i.e. the smallest Pythagorean field containing
is its Pythagorean closure (i.e. the smallest Pythagorean field containing 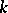 ), the sequence
), the sequence
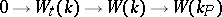 |
is exact (in addition, if 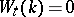 , the field
, the field 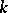 is Pythagorean);
is Pythagorean);
3) If 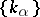 is the family of real closures of
is the family of real closures of 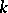 , the following sequence is exact:
, the following sequence is exact:
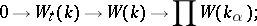 |
in particular,
4) If 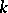 is not a real field, the group
is not a real field, the group  is torsion.
is torsion.
A number of other results concern the multiplicative theory of forms. In particular, let 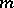 be the set of types of quadratic forms on even-dimensional spaces. Then
be the set of types of quadratic forms on even-dimensional spaces. Then 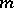 will be a two-sided ideal in
will be a two-sided ideal in 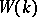 , and
, and 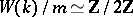 ; the ideal
; the ideal 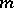 will contain all zero divisors of
will contain all zero divisors of 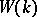 ; the set of nilpotent elements of
; the set of nilpotent elements of 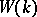 coincides with the set of elements of finite order of
coincides with the set of elements of finite order of 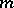 and is the Jacobson radical and the primary radical of
and is the Jacobson radical and the primary radical of 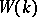 . The ring
. The ring 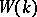 is finite if and only if
is finite if and only if 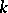 is not real while the group
is not real while the group 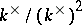 is finite; the ring
is finite; the ring 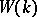 is Noetherian if and only if the group
is Noetherian if and only if the group 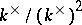 is finite. If
is finite. If 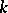 is not a real field,
is not a real field, 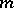 is the unique prime ideal of
is the unique prime ideal of 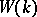 . If, on the contrary,
. If, on the contrary, 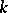 is a real field, the set of prime ideals of
is a real field, the set of prime ideals of 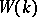 is the disjoint union of the ideal
is the disjoint union of the ideal 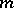 and the families of prime ideals corresponding to orders
and the families of prime ideals corresponding to orders 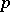 of
of 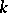 :
:
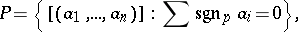 |
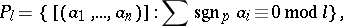 |
where 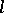 runs through the set of prime numbers, and
runs through the set of prime numbers, and 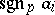 denotes the sign of the element
denotes the sign of the element 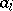 for the order
for the order 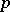 .
.
If 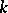 is a ring with involution, a construction analogous to that of a Witt ring leads to the concept of the group of a Witt ring with involution.
is a ring with involution, a construction analogous to that of a Witt ring leads to the concept of the group of a Witt ring with involution.
From a broader point of view, the Witt ring (group) is one of the first examples of a 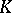 -functor (cf. Algebraic
-functor (cf. Algebraic 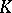 -theory), which play an important role in unitary algebraic
-theory), which play an important role in unitary algebraic 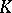 -theory.
-theory.
References
| [1] | E. Witt, "Theorie der quadratischen Formen in beliebigen Körpern" J. Reine Angew. Math. , 176 (1937) pp. 31–44 Zbl 0015.05701 Zbl 62.0106.02 |
| [2] | N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Addison-Wesley (1973) pp. Chapts. 1–2 (Translated from French) MR2333539 MR2327161 MR2325344 MR2284892 MR2109105 MR1994218 MR1890629 MR1728312 MR1727844 MR1727221 MR1080964 MR0979982 MR0979760 MR0979493 MR0928386 MR0682756 MR0524568 MR0573069 MR0354207 MR0360549 Zbl 05948094 Zbl 1105.18001 Zbl 1107.13002 Zbl 1107.13001 Zbl 1139.12001 Zbl 1111.00001 Zbl 1103.13003 Zbl 1103.13002 Zbl 1103.13001 Zbl 1017.12001 Zbl 1101.13300 Zbl 0902.13001 Zbl 0904.00001 Zbl 0719.12001 Zbl 0673.00001 Zbl 0666.13001 Zbl 0623.18008 Zbl 0281.00006 Zbl 0279.13001 Zbl 0238.13002 |
| [3] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
| [4] | F. Lorenz, "Quadratische Formen über Körpern" , Springer (1970) MR0282955 Zbl 0211.35303 |
| [5] | O.T. O'Meara, "Introduction to quadratic forms" , Springer (1973) Zbl 0259.10018 |
| [6] | T.Y. Lam, "The algebraic theory of quadratic forms" , Benjamin (1973) MR0396410 Zbl 0259.10019 |
| [7] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) MR0506372 Zbl 0292.10016 |
Comments
Given two vector spaces 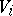 with bilinear forms
with bilinear forms 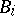 ,
, 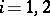 , the tensor product is the tensor product
, the tensor product is the tensor product 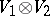 with the bilinear form defined by
with the bilinear form defined by
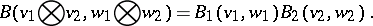 |
Witt ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Witt_ring&oldid=39953