Extension of a module

Any module containing the given module as a submodule. Usually one fixes a quotient module , that is, an extension of the module by the module is an exact sequence

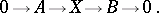Such a module always exists (for example, the direct sum of and 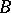), but need not be uniquely determined by 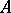and . Both in the theory of modules and in its applications there is a need to describe all different extensions of a module 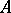by a module 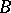. To this end one defines an equivalence relation on the class of all extensions of 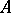by 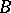as well as a binary operation (called Baer multiplication) on the set of equivalence classes, which thus becomes an Abelian group 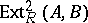, where 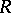is the ring over which 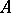is a module. 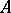This construction can be extended to -fold extensions of by 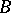, i.e. to exact sequences of the form

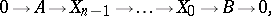corresponding to the group 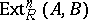. The groups

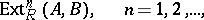are the derived functors of the functor 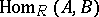, and may be computed using a projective resolution of or an injective resolution of 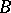. An extension 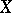of is called essential if 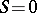is the only submodule of with . Every module has a maximal essential extension and this is the minimal injective module containing the given one.

For references see Extension of a group.

Comments

The minimal injective module containing 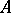is called the injective hull or envelope of . The notion can be defined in any Abelian category, cf. [a1]. The dual notion is that of a projective cover.

References

[a1]	C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973)