Difference between revisions of "Coherent algebra"
m (Link) |
(links) |
||
| Line 11: | Line 11: | ||
<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014012.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014013.png" /> is the all-one matrix; | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014012.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014013.png" /> is the all-one matrix; | ||
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014014.png" /> is closed with respect to [[Schur–Hadamard multiplication]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014015.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014016.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014017.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014018.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014019.png" />. Each coherent algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014020.png" /> has a unique basis of zero-one matrices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014021.png" /> such that: | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014014.png" /> is closed with respect to [[Schur–Hadamard multiplication]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014015.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014016.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014017.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014018.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014019.png" />. |
| + | |||
| + | Each coherent algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014020.png" /> has a unique basis of zero-one matrices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014021.png" /> such that: | ||
1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014022.png" />; | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014022.png" />; | ||
| Line 17: | Line 19: | ||
2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014023.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014024.png" /> is the matrix transposed to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014025.png" />; | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014023.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014024.png" /> is the matrix transposed to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014025.png" />; | ||
| − | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014026.png" />. Property 1) implies that the basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014027.png" /> consists of mutually orthogonal idempotents with respect to the Schur–Hadamard product. This basis is called the standard basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014028.png" />. The non-negative integer structure | + | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014026.png" />. |
| + | |||
| + | Property 1) implies that the basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014027.png" /> consists of mutually orthogonal idempotents with respect to the Schur–Hadamard product. This basis is called the standard basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014028.png" />. The non-negative integer [[structure constant]]s <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014029.png" /> are important numerical invariants of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014030.png" />. The notation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014031.png" /> indicates that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014032.png" /> is a coherent algebra with standard basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014033.png" />. | ||
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014034.png" /> and denote by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014035.png" /> a binary relation over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014036.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014037.png" /> is called the support of the zero-one matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014038.png" /> (or, in other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014039.png" /> is the [[adjacency matrix]] of the graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014040.png" /> with vertex set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014041.png" /> and set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014042.png" /> of directed edges). The system of relations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014043.png" /> obtained in this way from a coherent algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014044.png" /> is called a coherent configuration. | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014034.png" /> and denote by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014035.png" /> a binary relation over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014036.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014037.png" /> is called the support of the zero-one matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014038.png" /> (or, in other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014039.png" /> is the [[adjacency matrix]] of the graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014040.png" /> with vertex set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014041.png" /> and set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014042.png" /> of directed edges). The system of relations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014043.png" /> obtained in this way from a coherent algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014044.png" /> is called a coherent configuration. | ||
| Line 35: | Line 39: | ||
and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014059.png" /> is a minimal (with respect to inclusion) subset satisfying condition (a1). The coherent algebras with one fibre are exactly the BM-algebras. Coherent algebras with few fibres may be used for a unified presentation and investigation of various combinatorial objects, see, for example, [[#References|[a3]]], [[#References|[a7]]], [[#References|[a9]]]. | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014059.png" /> is a minimal (with respect to inclusion) subset satisfying condition (a1). The coherent algebras with one fibre are exactly the BM-algebras. Coherent algebras with few fibres may be used for a unified presentation and investigation of various combinatorial objects, see, for example, [[#References|[a3]]], [[#References|[a7]]], [[#References|[a9]]]. | ||
| − | An important class of coherent algebras consists of the centralizer algebras of permutation groups (not necessarily transitive) [[#References|[a2]]], [[#References|[a10]]] (cf. also [[ | + | An important class of coherent algebras consists of the centralizer algebras of permutation groups (not necessarily transitive) [[#References|[a2]]], [[#References|[a10]]] (cf. also [[Permutation group]]; [[Centralizer]]). This leads to many important applications of coherent algebras. |
It was Higman [[#References|[a5]]], [[#References|[a8]]] who developed the foundations of the representation theory of coherent algebras as a generalization of the representation theory of finite permutation groups (cf. also [[Finite group, representation of a|Finite group, representation of a]]). | It was Higman [[#References|[a5]]], [[#References|[a8]]] who developed the foundations of the representation theory of coherent algebras as a generalization of the representation theory of finite permutation groups (cf. also [[Finite group, representation of a|Finite group, representation of a]]). | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Bannai, T. Ito, "Algebraic combinatorics" , '''I''' , Benjamin/Cummings (1984)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.A. Faradžev, M.H. Klin, M.E. Muzichuk, "Cellular rings and groups of automorphisms of graphs" I.A. Faradžev (ed.) et al. (ed.) , ''Investigations in Algebraic Theory of Combinatorial Objects'' , Kluwer Acad. Publ. (1994) pp. 1–152</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W.H. Haemers, D.G. Higman, "Strongly regular graphs with strongly regular decomposition" ''Linear Alg. & Its Appl.'' , '''114/115''' (1989) pp. 379–398</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D.G. Higman, "Coherent configurations I" ''Rend. Sem. Mat. Univ. Padova'' , '''44''' (1970) pp. 1–25</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D.G. Higman, "Coherent configurations, Part I: Ordinary representation theory" ''Geom. Dedicata'' , '''4''' (1975) pp. 1–32</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> D.G. Higman, "Coherent algebras" ''Linear Alg. & Its Appl.'' , '''93''' (1987) pp. 209–239</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> D.G. Higman, "Strongly regular designs and coherent configurations of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014060.png" />" ''Europ. J. Combin.'' , '''9''' (1988) pp. 411–422</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> D.G. Higman, "Computations related to coherent configurations" ''Congr. Numer.'' , '''75''' (1990) pp. 9–20</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> M.E. Muzychuk, M. Klin, "On graphs with three eigenvalues" ''Discr. Math.'' , '''189''' (1998) pp. 191–207</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> H. Wielandt, "Finite permutation groups" , Acad. Press (1964)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Bannai, T. Ito, "Algebraic combinatorics" , '''I''' , Benjamin/Cummings (1984)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> I.A. Faradžev, M.H. Klin, M.E. Muzichuk, "Cellular rings and groups of automorphisms of graphs" I.A. Faradžev (ed.) et al. (ed.) , ''Investigations in Algebraic Theory of Combinatorial Objects'' , Kluwer Acad. Publ. (1994) pp. 1–152</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> W.H. Haemers, D.G. Higman, "Strongly regular graphs with strongly regular decomposition" ''Linear Alg. & Its Appl.'' , '''114/115''' (1989) pp. 379–398</TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> D.G. Higman, "Coherent configurations I" ''Rend. Sem. Mat. Univ. Padova'' , '''44''' (1970) pp. 1–25</TD></TR> | ||
| + | <TR><TD valign="top">[a5]</TD> <TD valign="top"> D.G. Higman, "Coherent configurations, Part I: Ordinary representation theory" ''Geom. Dedicata'' , '''4''' (1975) pp. 1–32</TD></TR> | ||
| + | <TR><TD valign="top">[a6]</TD> <TD valign="top"> D.G. Higman, "Coherent algebras" ''Linear Alg. & Its Appl.'' , '''93''' (1987) pp. 209–239</TD></TR> | ||
| + | <TR><TD valign="top">[a7]</TD> <TD valign="top"> D.G. Higman, "Strongly regular designs and coherent configurations of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130140/c13014060.png" />" ''Europ. J. Combin.'' , '''9''' (1988) pp. 411–422</TD></TR> | ||
| + | <TR><TD valign="top">[a8]</TD> <TD valign="top"> D.G. Higman, "Computations related to coherent configurations" ''Congr. Numer.'' , '''75''' (1990) pp. 9–20</TD></TR> | ||
| + | <TR><TD valign="top">[a9]</TD> <TD valign="top"> M.E. Muzychuk, M. Klin, "On graphs with three eigenvalues" ''Discr. Math.'' , '''189''' (1998) pp. 191–207</TD></TR> | ||
| + | <TR><TD valign="top">[a10]</TD> <TD valign="top"> H. Wielandt, "Finite permutation groups" , Acad. Press (1964)</TD></TR> | ||
| + | </table> | ||
Revision as of 06:50, 27 September 2016
Algebras introduced by D.G. Higman, first in relational language under the name coherent configuration [a4] and later in terms of matrices [a6]. The slightly different axiomatics of cellular algebras were independently suggested by B.Yu. Weisfeiler and A.A. Leman (cf. also Cellular algebra).
Like association schemes and Bose–Mesner algebras, coherent algebras provide a wide and solid foundation for investigations in various areas of algebraic combinatorics.
A coherent algebra  of order
of order  and rank
and rank  is a matrix subalgebra of the full matrix algebra
is a matrix subalgebra of the full matrix algebra  of
of  -matrices over
-matrices over  such that:
such that:
 is closed with respect to the Hermitian adjoint, which is defined by
is closed with respect to the Hermitian adjoint, which is defined by  for
for  ;
;
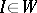 , where
, where 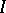 is the unit matrix;
is the unit matrix;
 , where
, where  is the all-one matrix;
is the all-one matrix;
 is closed with respect to Schur–Hadamard multiplication
is closed with respect to Schur–Hadamard multiplication  , where
, where 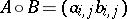 for
for  ,
, 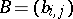 ,
,  .
.
Each coherent algebra  has a unique basis of zero-one matrices
has a unique basis of zero-one matrices  such that:
such that:
1)  ;
;
2)  , where
, where  is the matrix transposed to
is the matrix transposed to  ;
;
3) 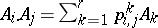 .
.
Property 1) implies that the basis  consists of mutually orthogonal idempotents with respect to the Schur–Hadamard product. This basis is called the standard basis of
consists of mutually orthogonal idempotents with respect to the Schur–Hadamard product. This basis is called the standard basis of 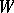 . The non-negative integer structure constants
. The non-negative integer structure constants  are important numerical invariants of
are important numerical invariants of  . The notation
. The notation  indicates that
indicates that  is a coherent algebra with standard basis
is a coherent algebra with standard basis  .
.
Let 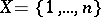 and denote by
and denote by 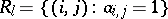 a binary relation over
a binary relation over  .
. 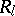 is called the support of the zero-one matrix
is called the support of the zero-one matrix  (or, in other words,
(or, in other words,  is the adjacency matrix of the graph
is the adjacency matrix of the graph 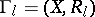 with vertex set
with vertex set 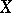 and set
and set 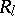 of directed edges). The system of relations
of directed edges). The system of relations  obtained in this way from a coherent algebra
obtained in this way from a coherent algebra  is called a coherent configuration.
is called a coherent configuration.
The structure constants  of
of  are sometimes called the intersection numbers of
are sometimes called the intersection numbers of  . They have the following combinatorial interpretation:
. They have the following combinatorial interpretation:
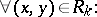 |
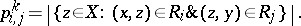 |
A coherent configuration  is called homogeneous if one of its basic relations, say
is called homogeneous if one of its basic relations, say  , coincides with the diagonal relation
, coincides with the diagonal relation  . In terms of matrices, a coherent algebra
. In terms of matrices, a coherent algebra 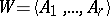 is called a Bose–Mesner algebra (briefly BM-algebra) if
is called a Bose–Mesner algebra (briefly BM-algebra) if  . Note that according to E. Bannai and T. Ito [a1], a homogeneous coherent configuration is also called an association scheme (not necessarily commutative; cf. also Association scheme).
. Note that according to E. Bannai and T. Ito [a1], a homogeneous coherent configuration is also called an association scheme (not necessarily commutative; cf. also Association scheme).
Let  be a coherent configuration. A subset
be a coherent configuration. A subset 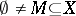 is called a fibre of
is called a fibre of  if
if
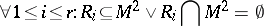 | (a1) |
and  is a minimal (with respect to inclusion) subset satisfying condition (a1). The coherent algebras with one fibre are exactly the BM-algebras. Coherent algebras with few fibres may be used for a unified presentation and investigation of various combinatorial objects, see, for example, [a3], [a7], [a9].
is a minimal (with respect to inclusion) subset satisfying condition (a1). The coherent algebras with one fibre are exactly the BM-algebras. Coherent algebras with few fibres may be used for a unified presentation and investigation of various combinatorial objects, see, for example, [a3], [a7], [a9].
An important class of coherent algebras consists of the centralizer algebras of permutation groups (not necessarily transitive) [a2], [a10] (cf. also Permutation group; Centralizer). This leads to many important applications of coherent algebras.
It was Higman [a5], [a8] who developed the foundations of the representation theory of coherent algebras as a generalization of the representation theory of finite permutation groups (cf. also Finite group, representation of a).
References
| [a1] | E. Bannai, T. Ito, "Algebraic combinatorics" , I , Benjamin/Cummings (1984) |
| [a2] | I.A. Faradžev, M.H. Klin, M.E. Muzichuk, "Cellular rings and groups of automorphisms of graphs" I.A. Faradžev (ed.) et al. (ed.) , Investigations in Algebraic Theory of Combinatorial Objects , Kluwer Acad. Publ. (1994) pp. 1–152 |
| [a3] | W.H. Haemers, D.G. Higman, "Strongly regular graphs with strongly regular decomposition" Linear Alg. & Its Appl. , 114/115 (1989) pp. 379–398 |
| [a4] | D.G. Higman, "Coherent configurations I" Rend. Sem. Mat. Univ. Padova , 44 (1970) pp. 1–25 |
| [a5] | D.G. Higman, "Coherent configurations, Part I: Ordinary representation theory" Geom. Dedicata , 4 (1975) pp. 1–32 |
| [a6] | D.G. Higman, "Coherent algebras" Linear Alg. & Its Appl. , 93 (1987) pp. 209–239 |
| [a7] | D.G. Higman, "Strongly regular designs and coherent configurations of type 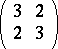 " Europ. J. Combin. , 9 (1988) pp. 411–422 " Europ. J. Combin. , 9 (1988) pp. 411–422 |
| [a8] | D.G. Higman, "Computations related to coherent configurations" Congr. Numer. , 75 (1990) pp. 9–20 |
| [a9] | M.E. Muzychuk, M. Klin, "On graphs with three eigenvalues" Discr. Math. , 189 (1998) pp. 191–207 |
| [a10] | H. Wielandt, "Finite permutation groups" , Acad. Press (1964) |
Coherent algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Coherent_algebra&oldid=39321