Difference between revisions of "Pontryagin maximum principle"
m (links) |
(some more TeX) |
||
| Line 7: | Line 7: | ||
\dot{x}=f(x,u), | \dot{x}=f(x,u), | ||
\end{equation} | \end{equation} | ||
| − | where | + | where $x\in\mathbb{R}^n$ is a phase vector, $u\in\mathbb{R}^p$ is a control parameter and $f$ is a [[Continuous function|continuous]] [[vector function]] in the variables $x$, $u$ that is continuously differentiable with respect to $x$. A certain set $U$ of admissible values of the control parameter $u$ in the space $\mathbb{R}^p$ is given; two points $x^0$ and $x^1$ in the [[phase space]] $\mathbb{R}^n$ are given; the initial time $t_0$ is fixed. Any piecewise-continuous function $u(t)$, $t_0\leq t\leq t_1$, with values in $U$, is called an admissible control. One says that an admissible control $u=u(t)$ transfers the phase point from the position $x^0$ to the position $x^1$ ($x^0\rightarrow x^1$) if the corresponding solution $x(t)$ of the system \eqref{eq:1} satisfying the initial condition $x(t_0)=x^0$ is defined for all $t\in[t_0,t_1]$ and if $x(t_1)=x^1$. Among all admissible controls transferring the phase point from the position $x^0$ to the position $x^1$ it is required to find an optimal control, i.e. a function $u^*(t)$ for which the [[functional]] |
| − | + | \begin{equation}\label{eq:2} | |
| − | + | J=\int_{t_0}^{t_1}f^0(x(t),u(t))dt | |
| − | + | \end{equation} | |
| − | takes least possible value. Here | + | takes least possible value. Here $f^0(x,u)$ is a given function from the same class as $f(x,u)$, $x(t)$ is the solution of the system \eqref{eq:1} with the initial condition $x(t_0)=x^0$ corresponding to the control $u(t)$, and $t_1$ is the time at which this solution passes through $x^1$. The problem consists of finding a pair consisting of the optimal control $u^*(t)$ and the corresponding optimal trajectory $x^*(t)$ of \eqref{eq:1}. |
Let | Let | ||
| + | \begin{equation} | ||
| + | H(\psi,x,u)=(\psi,\mathbf{f}(x,u)) | ||
| + | \end{equation} | ||
| + | be a scalar function ([[Hamiltonian]]) of the variables $\psi$, $x$, $u$, where $\psi=(\psi_0,\psi^1)\in\mathbb{R}^{n+1}$, $\psi_0\in\mathbb{R}^1$, $\psi^1\in\mathbb{R}^n$, $\mathbf{f}=(f_0,f)$. To the function $H(\psi,x,u)$ corresponds a canonical [[Hamiltonian system]] (with respect to $\psi$, $x$) | ||
| + | \begin{equation}\label{eq:3} | ||
| + | \frac{dx}{dt}=\frac{\partial H}{\partial\psi},\quad\frac{d\psi}{dt}=-\frac{\partial H}{\partial x}, | ||
| + | \end{equation} | ||
| + | (the first equation in \eqref{eq:3} is the system \eqref{eq:1}). Let | ||
| + | \begin{equation} | ||
| + | M(\psi,x)=\sup\{H(\psi,x,u)\colon u\in U\}. | ||
| + | \end{equation} | ||
| − | + | The Pontryagin maximum principle states: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378048.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378049.png" />) is a solution of the optimal control problem \eqref{eq:1}, \eqref{eq:2} (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378050.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378051.png" />), then there exists a non-zero absolutely-continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378052.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378053.png" /> satisfy system \eqref{eq:3} in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378054.png" />, such that for almost-all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378055.png" /> the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378056.png" /> attains its maximum: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The Pontryagin maximum principle states: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378048.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378049.png" />) is a solution of the optimal control problem \eqref{eq:1}, | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378057.png" /></td> <td valign="top" style="width:5%;text-align:right;">(4)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378057.png" /></td> <td valign="top" style="width:5%;text-align:right;">(4)</td></tr></table> | ||
| Line 35: | Line 36: | ||
are satisfied. | are satisfied. | ||
| − | If the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378060.png" /> satisfy the relations | + | If the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378060.png" /> satisfy the relations \eqref{eq:3}, (4) (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378061.png" /> are Pontryagin extremal), then the conditions |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378062.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378062.png" /></td> </tr></table> | ||
| Line 45: | Line 46: | ||
Admitting closed sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378068.png" /> (in particular, these regions can be determined by systems of non-strict inequalities) makes the problem under consideration non-classical. The fundamental necessary conditions from the classical calculus of variations with ordinary derivative follow from the Pontryagin maximum principle (see <ref name="Pontryagin" /> and also [[Weierstrass conditions (for a variational extremum)|Weierstrass conditions (for a variational extremum)]]). | Admitting closed sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378068.png" /> (in particular, these regions can be determined by systems of non-strict inequalities) makes the problem under consideration non-classical. The fundamental necessary conditions from the classical calculus of variations with ordinary derivative follow from the Pontryagin maximum principle (see <ref name="Pontryagin" /> and also [[Weierstrass conditions (for a variational extremum)|Weierstrass conditions (for a variational extremum)]]). | ||
| − | A widely used proof of the above formulation of the Pontryagin maximum principle, based on needle variations (i.e. one considers admissible controls arbitrarily deviating from the optimal one but only on a finite number of small time intervals), consists of linearization of the problem in a neighbourhood of the optimal solution, construction of a convex cone of variations of the optimal trajectory, and subsequent application of the theorem on separated convex cones <ref name="Pontryagin" />. The corresponding condition is then rewritten in the analytical form | + | A widely used proof of the above formulation of the Pontryagin maximum principle, based on needle variations (i.e. one considers admissible controls arbitrarily deviating from the optimal one but only on a finite number of small time intervals), consists of linearization of the problem in a neighbourhood of the optimal solution, construction of a convex cone of variations of the optimal trajectory, and subsequent application of the theorem on separated convex cones <ref name="Pontryagin" />. The corresponding condition is then rewritten in the analytical form \eqref{eq:3}, (4) in terms of the maximum of the Hamiltonian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378069.png" /> of the phase variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378070.png" />, the controls <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378071.png" /> and the adjoint variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073780/p07378072.png" />, which play the same role as the [[Lagrange multipliers|Lagrange multipliers]] in the classical calculus of variations. Effective application of the Pontryagin maximum principle often necessitates the solution of a two-point boundary value problem for \eqref{eq:3}. |
The most complete solution of the problem of optimal control was obtained in the case of certain linear systems, for which the relations in the Pontryagin maximum principle are not only necessary but also sufficient optimality conditions. | The most complete solution of the problem of optimal control was obtained in the case of certain linear systems, for which the relations in the Pontryagin maximum principle are not only necessary but also sufficient optimality conditions. | ||
Revision as of 16:57, 7 June 2016
Relations describing necessary conditions for a strong maximum in a non-classical variational problem in the mathematical theory of optimal control. It was first formulated in 1956 by L.S. Pontryagin [1].
The proposed formulation of the Pontryagin maximum principle corresponds to the following problem of optimal control. Given a system of ordinary differential equations \begin{equation}\label{eq:1} \dot{x}=f(x,u), \end{equation} where $x\in\mathbb{R}^n$ is a phase vector, $u\in\mathbb{R}^p$ is a control parameter and $f$ is a continuous vector function in the variables $x$, $u$ that is continuously differentiable with respect to $x$. A certain set $U$ of admissible values of the control parameter $u$ in the space $\mathbb{R}^p$ is given; two points $x^0$ and $x^1$ in the phase space $\mathbb{R}^n$ are given; the initial time $t_0$ is fixed. Any piecewise-continuous function $u(t)$, $t_0\leq t\leq t_1$, with values in $U$, is called an admissible control. One says that an admissible control $u=u(t)$ transfers the phase point from the position $x^0$ to the position $x^1$ ($x^0\rightarrow x^1$) if the corresponding solution $x(t)$ of the system \eqref{eq:1} satisfying the initial condition $x(t_0)=x^0$ is defined for all $t\in[t_0,t_1]$ and if $x(t_1)=x^1$. Among all admissible controls transferring the phase point from the position $x^0$ to the position $x^1$ it is required to find an optimal control, i.e. a function $u^*(t)$ for which the functional \begin{equation}\label{eq:2} J=\int_{t_0}^{t_1}f^0(x(t),u(t))dt \end{equation} takes least possible value. Here $f^0(x,u)$ is a given function from the same class as $f(x,u)$, $x(t)$ is the solution of the system \eqref{eq:1} with the initial condition $x(t_0)=x^0$ corresponding to the control $u(t)$, and $t_1$ is the time at which this solution passes through $x^1$. The problem consists of finding a pair consisting of the optimal control $u^*(t)$ and the corresponding optimal trajectory $x^*(t)$ of \eqref{eq:1}.
Let \begin{equation} H(\psi,x,u)=(\psi,\mathbf{f}(x,u)) \end{equation} be a scalar function (Hamiltonian) of the variables $\psi$, $x$, $u$, where $\psi=(\psi_0,\psi^1)\in\mathbb{R}^{n+1}$, $\psi_0\in\mathbb{R}^1$, $\psi^1\in\mathbb{R}^n$, $\mathbf{f}=(f_0,f)$. To the function $H(\psi,x,u)$ corresponds a canonical Hamiltonian system (with respect to $\psi$, $x$) \begin{equation}\label{eq:3} \frac{dx}{dt}=\frac{\partial H}{\partial\psi},\quad\frac{d\psi}{dt}=-\frac{\partial H}{\partial x}, \end{equation} (the first equation in \eqref{eq:3} is the system \eqref{eq:1}). Let \begin{equation} M(\psi,x)=\sup\{H(\psi,x,u)\colon u\in U\}. \end{equation}
The Pontryagin maximum principle states: If 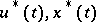 (
(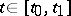 ) is a solution of the optimal control problem \eqref{eq:1}, \eqref{eq:2} (
) is a solution of the optimal control problem \eqref{eq:1}, \eqref{eq:2} (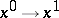 ,
, 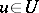 ), then there exists a non-zero absolutely-continuous function
), then there exists a non-zero absolutely-continuous function 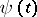 such that
such that 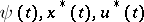 satisfy system \eqref{eq:3} in
satisfy system \eqref{eq:3} in 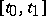 , such that for almost-all
, such that for almost-all 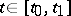 the function
the function 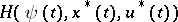 attains its maximum:
attains its maximum:
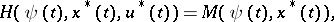 | (4) |
and such that at the terminal time 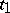 the conditions
the conditions
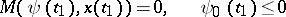 | (5) |
are satisfied.
If the functions 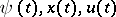 satisfy the relations \eqref{eq:3}, (4) (i.e.
satisfy the relations \eqref{eq:3}, (4) (i.e. 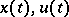 are Pontryagin extremal), then the conditions
are Pontryagin extremal), then the conditions
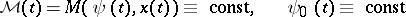 |
hold.
From the above statement follows the maximum principle for the time-optimal problem (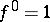 ,
, 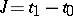 ). This statement admits a natural generalization to non-autonomous systems, problems with variable end-points and problems with restricted phase coordinates (
). This statement admits a natural generalization to non-autonomous systems, problems with variable end-points and problems with restricted phase coordinates (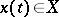 , where
, where 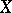 is a closed set in the phase space
is a closed set in the phase space 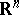 satisfying some additional restrictions [1].
satisfying some additional restrictions [1].
Admitting closed sets 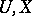 (in particular, these regions can be determined by systems of non-strict inequalities) makes the problem under consideration non-classical. The fundamental necessary conditions from the classical calculus of variations with ordinary derivative follow from the Pontryagin maximum principle (see [1] and also Weierstrass conditions (for a variational extremum)).
(in particular, these regions can be determined by systems of non-strict inequalities) makes the problem under consideration non-classical. The fundamental necessary conditions from the classical calculus of variations with ordinary derivative follow from the Pontryagin maximum principle (see [1] and also Weierstrass conditions (for a variational extremum)).
A widely used proof of the above formulation of the Pontryagin maximum principle, based on needle variations (i.e. one considers admissible controls arbitrarily deviating from the optimal one but only on a finite number of small time intervals), consists of linearization of the problem in a neighbourhood of the optimal solution, construction of a convex cone of variations of the optimal trajectory, and subsequent application of the theorem on separated convex cones [1]. The corresponding condition is then rewritten in the analytical form \eqref{eq:3}, (4) in terms of the maximum of the Hamiltonian 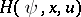 of the phase variables
of the phase variables  , the controls
, the controls  and the adjoint variables
and the adjoint variables 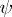 , which play the same role as the Lagrange multipliers in the classical calculus of variations. Effective application of the Pontryagin maximum principle often necessitates the solution of a two-point boundary value problem for \eqref{eq:3}.
, which play the same role as the Lagrange multipliers in the classical calculus of variations. Effective application of the Pontryagin maximum principle often necessitates the solution of a two-point boundary value problem for \eqref{eq:3}.
The most complete solution of the problem of optimal control was obtained in the case of certain linear systems, for which the relations in the Pontryagin maximum principle are not only necessary but also sufficient optimality conditions.
There are numerous generalizations of the Pontryagin maximum principle; for instance, in the direction of more complicated non-classical constraints (including mixed constraints imposed on the controls and phase coordinates, functional and different integral constraints), in studies of the sufficiency of the corresponding constraints, in the consideration of generalized solutions, so-called sliding regimes, systems of differential equations with non-smooth right-hand side, differential inclusions, optimal control problems for discrete systems and systems with an infinite number of degrees of freedom, in particular, described by partial differential equations, equations with an after effect (including equations with a delay), evolution equations in a Banach space, etc. The latter lead to new classes of variations of the corresponding functionals, the introduction of the so-called integral maximum principle, the linearized maximum principle, etc. Rather general classes of variational problems with non-classical constraints (including non-strict inequalities) or with non-smooth functionals are usually called problems of Pontryagin type. The discovery of the Pontryagin maximum principle initiated the development of mathematical optimal control theory. It stimulated new research in the field of differential equations, functional analysis and extremal problems, computational mathematics and other related domains.
Comments
In the Western literature the Pontryagin maximum principle is also simply known as the minimum principle. (Cf. Optimal control, mathematical theory of)
References
| [a1] | W.H. Fleming, R.W. Rishel, "Deterministic and stochastic optimal control" , Springer (1975) |
| [a2] | L. Markus, "Foundations of optimal control theory" , Wiley (1967) |
| [a3] | L.D. Berkovitz, "Optimal control theory" , Springer (1974) |
| [a4] | L. Cesari, "Optimization - Theory and applications" , Springer (1983) |
| [a5] | F. Clarke, "Optimization and nonsmooth analysis" , Wiley (1983) |
Pontryagin maximum principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pontryagin_maximum_principle&oldid=38943