Difference between revisions of "Cauchy Schwarz inequality"
m (Camillo.delellis moved page Cauchy inequality to Cauchy Schwarz inequality: More common name) |
(some TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|part}} | ||
| + | |||
The Cauchy inequality for finite sums of real numbers is the inequality | The Cauchy inequality for finite sums of real numbers is the inequality | ||
| + | \begin{equation} | ||
| + | \left(\sum_{k=1}^n a_k b_k\right)^2\leq \sum_{k=1}^n a_k^2 \sum_{k=1}^n b_k^2 . | ||
| + | \end{equation} | ||
| + | Proved by A.L. Cauchy (1821); the analogue for integrals is known as the [[Bunyakovskii inequality]]. | ||
| − | + | The Cauchy inequality is also the name used for an inequality for the [[modulus]] $|f^{(k)}(a)|$ of a derivative of a regular [[analytic function]] $f(z)$ at a [[fixed point]] $a$ of the complex plane $C$, or for the modulus $|c_k|$ of the coefficients of the [[power series]] expansion of $f(z)$, | |
| − | + | \begin{equation} | |
| − | + | f(z)=\sum_{k=0}^\infty c_k (z-a)^k . | |
| − | + | \end{equation} | |
| − | The Cauchy inequality is also the name used for an inequality for the modulus | ||
| − | |||
| − | |||
| − | |||
These inequalities are | These inequalities are | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c0208809.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c0208809.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | ||
| − | where | + | where $r$ is the radius of any disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088011.png" /> on which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088012.png" /> is regular, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088013.png" /> is the maximum modulus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088014.png" /> on the circle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088015.png" />. The inequalities (*) occur in the work of A.L. Cauchy (see e.g. ). They directly imply the Cauchy–Hadamard inequality (see ): |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088016.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088016.png" /></td> </tr></table> | ||
| Line 37: | Line 39: | ||
<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088033.png" /> are the radii of a polydisc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088034.png" /> on which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088035.png" /> is holomorphic, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088036.png" /> is the maximum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088037.png" /> on the distinguished boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088038.png" />. | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088033.png" /> are the radii of a polydisc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088034.png" /> on which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088035.png" /> is holomorphic, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088036.png" /> is the maximum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088037.png" /> on the distinguished boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088038.png" />. | ||
| − | For references see [[ | + | For references see [[Cauchy–Hadamard theorem]]. |
====Comments==== | ====Comments==== | ||
| − | |||
| − | The distinguished boundary of a polydisc | + | In Western literature the name Bunyakovskii inequality is rarely used. Both the inequality for finite sums of real numbers, or its generalization to complex numbers (see [[Bunyakovskii inequality]]), and its analogue for integrals are often called the Schwarz inequality or the Cauchy–Schwarz inequality. |
| + | |||
| + | The distinguished boundary of a [[polydisc]] $U^n$ as above is the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020880/c02088040.png" />. | ||
Revision as of 08:57, 31 May 2016
The Cauchy inequality for finite sums of real numbers is the inequality
\begin{equation}
\left(\sum_{k=1}^n a_k b_k\right)^2\leq \sum_{k=1}^n a_k^2 \sum_{k=1}^n b_k^2 .
\end{equation}
Proved by A.L. Cauchy (1821); the analogue for integrals is known as the Bunyakovskii inequality.
The Cauchy inequality is also the name used for an inequality for the modulus $|f^{(k)}(a)|$ of a derivative of a regular analytic function $f(z)$ at a fixed point $a$ of the complex plane $C$, or for the modulus $|c_k|$ of the coefficients of the power series expansion of $f(z)$, \begin{equation} f(z)=\sum_{k=0}^\infty c_k (z-a)^k . \end{equation} These inequalities are
 | (*) |
where $r$ is the radius of any disc 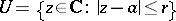 on which
on which 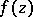 is regular, and
is regular, and  is the maximum modulus of
is the maximum modulus of 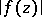 on the circle
on the circle  . The inequalities (*) occur in the work of A.L. Cauchy (see e.g. ). They directly imply the Cauchy–Hadamard inequality (see ):
. The inequalities (*) occur in the work of A.L. Cauchy (see e.g. ). They directly imply the Cauchy–Hadamard inequality (see ):
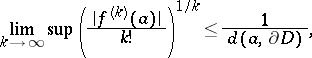 |
where 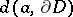 is the distance from
is the distance from  to the boundary
to the boundary 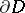 of the domain of holomorphy of
of the domain of holomorphy of  . In particular, if
. In particular, if  is an entire function, then at any point
is an entire function, then at any point  ,
,
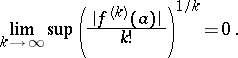 |
For a holomorphic function 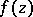 of several complex variables
of several complex variables 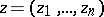 ,
, 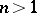 , the Cauchy inequalities are
, the Cauchy inequalities are
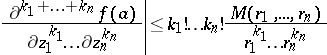 |
or
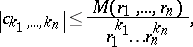 |
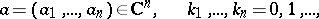 |
where  are the coefficients of the power series expansion of
are the coefficients of the power series expansion of 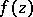 :
:
 |
 are the radii of a polydisc
are the radii of a polydisc 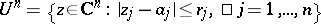 on which
on which  is holomorphic, and
is holomorphic, and 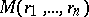 is the maximum of
is the maximum of 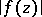 on the distinguished boundary of
on the distinguished boundary of  .
.
For references see Cauchy–Hadamard theorem.
Comments
In Western literature the name Bunyakovskii inequality is rarely used. Both the inequality for finite sums of real numbers, or its generalization to complex numbers (see Bunyakovskii inequality), and its analogue for integrals are often called the Schwarz inequality or the Cauchy–Schwarz inequality.
The distinguished boundary of a polydisc $U^n$ as above is the set  .
.
Cauchy Schwarz inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_Schwarz_inequality&oldid=38892