Difference between revisions of "Tensor on a vector space"
(Importing text file) |
m (link) |
||
| Line 45: | Line 45: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240080.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240080.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | ||
| − | Here, as often happens in tensor calculus, Einstein's summation convention is applied: with respect to any pair of equal indices of which one is an upper index and the other is a lower index, it is understood that summation from 1 to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240081.png" /> is carried out. Conversely, if a system of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240082.png" /> elements of a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240083.png" /> depending on the basis of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240084.png" /> is altered in the transition from one basis to another basis according to the formulas (1), then this system is the set of components of some tensor of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240085.png" />. | + | Here, as often happens in tensor calculus, Einstein's [[summation convention]] is applied: with respect to any pair of equal indices of which one is an upper index and the other is a lower index, it is understood that summation from 1 to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240081.png" /> is carried out. Conversely, if a system of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240082.png" /> elements of a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240083.png" /> depending on the basis of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240084.png" /> is altered in the transition from one basis to another basis according to the formulas (1), then this system is the set of components of some tensor of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240085.png" />. |
In the vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240086.png" /> the operations of addition of tensors and of multiplication of a tensor by a scalar from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240087.png" /> are defined. Under these operations the corresponding components are added, or multiplied by the scalar. The operation of multiplying tensors of different types is also defined; it is introduced as follows. There is a natural isomorphism of vector spaces | In the vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240086.png" /> the operations of addition of tensors and of multiplication of a tensor by a scalar from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092400/t09240087.png" /> are defined. Under these operations the corresponding components are added, or multiplied by the scalar. The operation of multiplying tensors of different types is also defined; it is introduced as follows. There is a natural isomorphism of vector spaces | ||
Revision as of 19:15, 21 January 2016
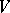 over a field
over a field 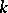
An element 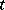 of the vector space
of the vector space
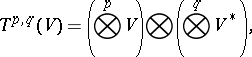 |
where  is the dual space of
is the dual space of 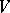 . The tensor
. The tensor 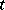 is said to be
is said to be  times contravariant and
times contravariant and 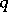 times covariant, or to be of type
times covariant, or to be of type 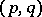 . The number
. The number 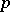 is called the contravariant valency, and
is called the contravariant valency, and 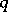 the covariant valency, while the number
the covariant valency, while the number 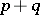 is called the general valency of the tensor
is called the general valency of the tensor 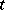 . The space
. The space 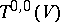 is identified with
is identified with 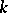 . Tensors of type
. Tensors of type 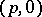 are called contravariant, those of the type
are called contravariant, those of the type 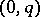 are called covariant, and the remaining ones are called mixed.
are called covariant, and the remaining ones are called mixed.
Examples of tensors.
1) A vector of the space  (a tensor of type
(a tensor of type 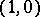 ).
).
2) A covector of the space 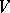 (a tensor of type
(a tensor of type  ).
).
3) Any covariant tensor
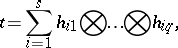 |
where 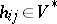 , defines a
, defines a 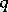 -linear form
-linear form 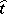 on
on  by the formula
by the formula
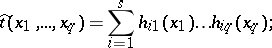 |
the mapping  from the space
from the space 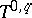 into the space
into the space 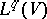 of all
of all 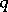 -linear forms on
-linear forms on 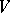 is linear and injective; if
is linear and injective; if 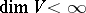 , then this mapping is an isomorphism, since any
, then this mapping is an isomorphism, since any  -linear form corresponds to some tensor of type
-linear form corresponds to some tensor of type  .
.
4) Similarly, a contravariant tensor in  defines a
defines a 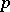 -linear form on
-linear form on 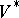 , and if
, and if 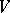 is finite dimensional, the converse is also true.
is finite dimensional, the converse is also true.
5) Every tensor
 |
where 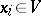 and
and 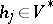 , defines a linear transformation
, defines a linear transformation 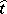 of the space
of the space  given by the formula
given by the formula
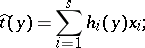 |
if 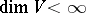 , any linear transformation of the space
, any linear transformation of the space 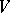 is defined by a tensor of type
is defined by a tensor of type 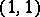 .
.
6) Similarly, any tensor of type 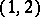 defines in
defines in 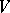 a bilinear operation, that is, the structure of a
a bilinear operation, that is, the structure of a 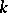 -algebra. Moreover, if
-algebra. Moreover, if 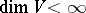 , then any
, then any 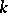 -algebra structure in
-algebra structure in 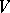 is defined by a tensor of type
is defined by a tensor of type 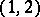 , called the structure tensor of the algebra.
, called the structure tensor of the algebra.
Let 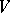 be finite dimensional, let
be finite dimensional, let  be a basis of it, and let
be a basis of it, and let  be the dual basis of the space
be the dual basis of the space  . Then the tensors
. Then the tensors
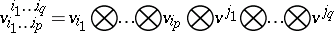 |
form a basis of the space  . The components
. The components 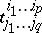 of a tensor
of a tensor 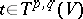 with respect to this basis are also called the components of the tensor
with respect to this basis are also called the components of the tensor 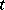 with respect to the basis
with respect to the basis  of the space
of the space 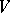 . For instance, the components of a vector and of a covector coincide with their usual coordinates with respect to the bases
. For instance, the components of a vector and of a covector coincide with their usual coordinates with respect to the bases 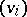 and
and 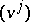 ; the components of a tensor of type
; the components of a tensor of type 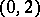 coincide with the entries of the matrix corresponding to the bilinear form; the components of a tensor of type
coincide with the entries of the matrix corresponding to the bilinear form; the components of a tensor of type 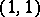 coincide with the entries of the matrix of the corresponding linear transformation, and the components of the structure tensor of an algebra coincide with its structure constants. If
coincide with the entries of the matrix of the corresponding linear transformation, and the components of the structure tensor of an algebra coincide with its structure constants. If  is another basis of
is another basis of 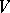 , with
, with 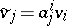 , and
, and 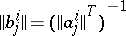 , then the components
, then the components  of the tensor
of the tensor 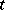 in this basis are defined by the formula
in this basis are defined by the formula
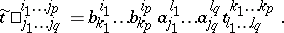 | (1) |
Here, as often happens in tensor calculus, Einstein's summation convention is applied: with respect to any pair of equal indices of which one is an upper index and the other is a lower index, it is understood that summation from 1 to  is carried out. Conversely, if a system of
is carried out. Conversely, if a system of 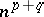 elements of a field
elements of a field 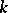 depending on the basis of the space
depending on the basis of the space 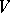 is altered in the transition from one basis to another basis according to the formulas (1), then this system is the set of components of some tensor of type
is altered in the transition from one basis to another basis according to the formulas (1), then this system is the set of components of some tensor of type 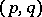 .
.
In the vector space 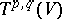 the operations of addition of tensors and of multiplication of a tensor by a scalar from
the operations of addition of tensors and of multiplication of a tensor by a scalar from 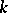 are defined. Under these operations the corresponding components are added, or multiplied by the scalar. The operation of multiplying tensors of different types is also defined; it is introduced as follows. There is a natural isomorphism of vector spaces
are defined. Under these operations the corresponding components are added, or multiplied by the scalar. The operation of multiplying tensors of different types is also defined; it is introduced as follows. There is a natural isomorphism of vector spaces
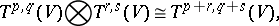 |
mapping
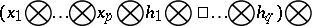 |
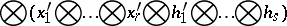 |
to
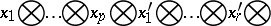 |
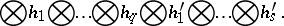 |
Consequently, for any 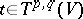 and
and 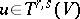 the element
the element 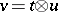 can be regarded as a tensor of type
can be regarded as a tensor of type 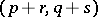 and is called the tensor product of
and is called the tensor product of 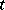 and
and  . The components of the product are computed according to the formula
. The components of the product are computed according to the formula
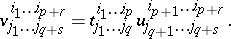 |
Let 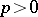 ,
, 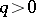 , and let the numbers
, and let the numbers 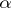 and
and 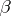 be fixed with
be fixed with 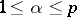 and
and 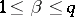 . Then there is a well-defined mapping
. Then there is a well-defined mapping 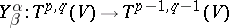 such that
such that
 |
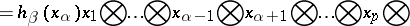 |
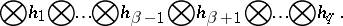 |
It is called contraction in the 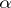 -th contravariant and the
-th contravariant and the 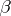 -th covariant indices. In components, the contraction is written in the form
-th covariant indices. In components, the contraction is written in the form
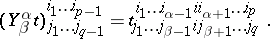 |
For instance, the contraction 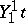 of a tensor of type
of a tensor of type 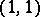 is the trace of the corresponding linear transformation.
is the trace of the corresponding linear transformation.
A tensor is similarly defined on an arbitrary unitary module  over an associative commutative ring with a unit. The stated examples and properties of tensors are transferred, with corresponding changes, to this case, it being sometimes necessary to assume that
over an associative commutative ring with a unit. The stated examples and properties of tensors are transferred, with corresponding changes, to this case, it being sometimes necessary to assume that  is a free or a finitely-generated free module.
is a free or a finitely-generated free module.
Let a non-degenerate bilinear form 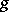 be fixed in a finite-dimensional vector space
be fixed in a finite-dimensional vector space 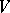 over a field
over a field 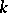 (for example,
(for example, 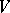 is a Euclidean or pseudo-Euclidean space over
is a Euclidean or pseudo-Euclidean space over 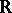 ); in this case the form
); in this case the form 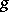 is called a metric tensor. A metric tensor defines an isomorphism
is called a metric tensor. A metric tensor defines an isomorphism 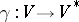 by the formula
by the formula
 |
Let 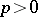 , and let the index
, and let the index 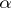 ,
,  , be fixed. Then the formula
, be fixed. Then the formula
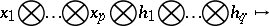 |
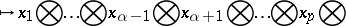 |
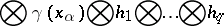 |
defines an isomorphism 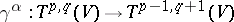 , called lowering of the
, called lowering of the 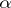 -th contravariant index. In other terms,
-th contravariant index. In other terms,
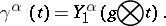 |
In components, lowering an index has the form
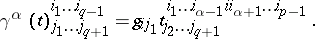 |
Similarly one defines the isomorphism of raising the 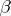 -th covariant index
-th covariant index  :
:
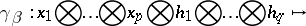 |
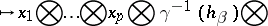 |
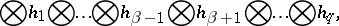 |
which maps 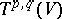 onto
onto 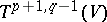 . In components, raising an index is written in the form
. In components, raising an index is written in the form
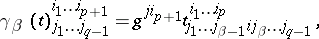 |
where 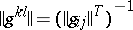 . In particular, raising at first the first, and then also the remaining covariant index of the metric tensor
. In particular, raising at first the first, and then also the remaining covariant index of the metric tensor 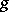 leads to a tensor of type
leads to a tensor of type 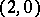 with components
with components 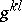 (a contravariant metric tensor). Sometimes the lowered (raised) index is not moved to the first (last) place, but is written in the same place in the lower (upper) group of indices, a point being put in the empty place which arises. For instance, for
(a contravariant metric tensor). Sometimes the lowered (raised) index is not moved to the first (last) place, but is written in the same place in the lower (upper) group of indices, a point being put in the empty place which arises. For instance, for 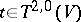 the components of the tensor
the components of the tensor 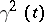 are written in the form
are written in the form 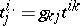 .
.
Any linear mapping 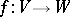 of vector spaces over
of vector spaces over 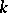 defines in a natural way linear mappings
defines in a natural way linear mappings
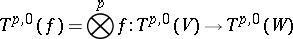 |
and
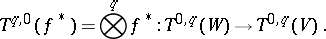 |
If 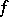 is an isomorphism, the linear mapping
is an isomorphism, the linear mapping
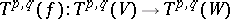 |
is also defined and 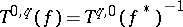 . The correspondence
. The correspondence 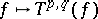 has functorial properties. In particular, it defines a linear representation
has functorial properties. In particular, it defines a linear representation 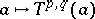 of the group
of the group 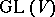 in the space
in the space 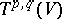 (the tensor representation).
(the tensor representation).
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [2] | I.M. Gel'fand, "Lectures on linear algebra" , Interscience (1961) (Translated from Russian) |
| [3] | A.I. Kostrikin, Yu.I. Manin, "Linear algebra and geometry" , Gordon & Breach (1989) (Translated from Russian) |
| [4] | M.M. Postnikov, "Linear algebra and differential geometry" , Moscow (1979) (In Russian) |
| [5] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
Tensor on a vector space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tensor_on_a_vector_space&oldid=37606