Difference between revisions of "Least common multiple"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | The smallest positive number among the common | + | The smallest positive number among the common [[multiple]]s of a finite set of integers or, in particular, of natural numbers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057750/l0577501.png" />. The least common multiple of the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057750/l0577502.png" /> exists if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057750/l0577503.png" />. It is usually denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057750/l0577504.png" />. |
Properties of the least common multiple are: | Properties of the least common multiple are: | ||
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R. Faure, A. Kaufman, M. Denis-Papin, "Mathématique nouvelles" , '''1–2''' , Dunod (1964)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> R. Faure, A. Kaufman, M. Denis-Papin, "Mathématique nouvelles" , '''1–2''' , Dunod (1964)</TD></TR> | ||
| + | </table> | ||
Revision as of 18:22, 16 January 2016
The smallest positive number among the common multiples of a finite set of integers or, in particular, of natural numbers,  . The least common multiple of the numbers
. The least common multiple of the numbers  exists if
exists if  . It is usually denoted by
. It is usually denoted by  .
.
Properties of the least common multiple are:
1) the least common multiple of  is a divisor of any other common multiple;
is a divisor of any other common multiple;
2)  ;
;
3) if the integers  are expressed as
are expressed as
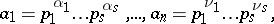 |
where  are distinct primes,
are distinct primes,  ,
, 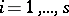 , and
, and 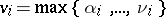 ,
, 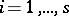 , then
, then
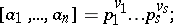 |
4) if 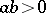 , then
, then 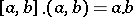 , where
, where 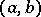 is the greatest common divisor of
is the greatest common divisor of  and
and 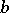 .
.
Thanks to the last property, the least common multiple of two numbers can be found with the aid of the Euclidean algorithm. The concept of the least common multiple can be defined for elements of an integral domain, and also for ideals of a commutative ring.
References
| [1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
| [2] | A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian) |
| [3] | R. Faure, A. Kaufman, M. Denis-Papin, "Mathématique nouvelles" , 1–2 , Dunod (1964) |
Comments
Other frequently used notations for the least common multiple are: 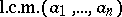 ,
, 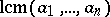 ,
, 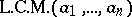 , etc. In a unique factorization domain least common multiples exist and are unique (up to units).
, etc. In a unique factorization domain least common multiples exist and are unique (up to units).
Least common multiple. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Least_common_multiple&oldid=37549