Difference between revisions of "Vizing theorem"
(Importing text file) |
m (links) |
||
| Line 11: | Line 11: | ||
In order to give reasonable upper bounds for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004048.png" />, Vizing [[#References|[a21]]] introduced the concept of list colouring: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004049.png" /> is the list-chromatic index of a graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004050.png" />, then, obviously, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004051.png" />. Vizing [[#References|[a21]]] even posed the still open (1999) list colouring conjecture: Every graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004052.png" /> satisfies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004053.png" />. With a surprisingly short proof, F. Galvin [[#References|[a1]]] showed that the list colouring conjecture is true for bipartite graphs. A.V. Kostochka [[#References|[a14]]] proved that if all cycles in a simple graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004054.png" /> are sufficiently long relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004055.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004056.png" />. If the list colouring conjecture is true, then, according to Vizing's theorem, the same bound would hold for any simple graph. | In order to give reasonable upper bounds for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004048.png" />, Vizing [[#References|[a21]]] introduced the concept of list colouring: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004049.png" /> is the list-chromatic index of a graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004050.png" />, then, obviously, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004051.png" />. Vizing [[#References|[a21]]] even posed the still open (1999) list colouring conjecture: Every graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004052.png" /> satisfies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004053.png" />. With a surprisingly short proof, F. Galvin [[#References|[a1]]] showed that the list colouring conjecture is true for bipartite graphs. A.V. Kostochka [[#References|[a14]]] proved that if all cycles in a simple graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004054.png" /> are sufficiently long relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004055.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004056.png" />. If the list colouring conjecture is true, then, according to Vizing's theorem, the same bound would hold for any simple graph. | ||
| − | The determination of the chromatic index can be transformed into a problem dealing with the chromatic number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004057.png" />. Namely, from the definition it is immediate that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004058.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004059.png" /> is the line graph of the simple graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004060.png" />. If, in addition, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004061.png" /> is the clique number (cf. also [[Fixed-point property|Fixed-point property]]) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004062.png" />, then Vizing's theorem implies | + | The determination of the chromatic index can be transformed into a problem dealing with the chromatic number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004057.png" />. Namely, from the definition it is immediate that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004058.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004059.png" /> is the [[line graph]] of the simple graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004060.png" />. If, in addition, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004061.png" /> is the clique number (cf. also [[Fixed-point property|Fixed-point property]]) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004062.png" />, then Vizing's theorem implies |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004063.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004063.png" /></td> </tr></table> | ||
| − | Therefore, this bound is called [[#References|[a16]]] the Vizing bound. L.W. Beineke [[#References|[a4]]] characterized line graphs by nine forbidden induced | + | Therefore, this bound is called [[#References|[a16]]] the Vizing bound. L.W. Beineke [[#References|[a4]]] characterized line graphs by nine forbidden [[induced subgraph]]s. Using only four forbidden induced subgraphs of Beineke's nine graphs, S.A. Choudom [[#References|[a8]]] determined two superclasses of line graphs for which the Vizing bound is also valid. Thus, since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004064.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004065.png" /> is not a triangle, Choudom's result extends Vizing's theorem. The most general contribution in this area was found by H. Randerath [[#References|[a16]]]: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004066.png" /> is a simple graph containing neither a complete <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004067.png" />-graph with an edge missing nor a claw <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004068.png" /> with one subdivided edge as an induced subgraph, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004069.png" /> is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004070.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004071.png" />. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> F. Galvin, "The list chromatic index of a bipartite multigraph" ''J. Combin. Th. B'' , '''68''' (1995) pp. 153–158</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Molloy, B. Reed, "A bound on the total chromatic number" ''Combinatorica'' , '''18''' (1998) pp. 241–280</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Behzad, "Graphs and their chromatic numbers" ''Doctoral Thesis Michigan State Univ.'' (1965)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> L.W. Beineke, "Derived graphs and digraphs" , ''Beiträge zur Graphentheorie'' , Teubner (1968) pp. 17–33</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> K.H. Chew, "On Vizing's theorem, adjacency lemma and fan argument generalized to multigraphs" ''Discrete Math.'' , '''171''' (1997) pp. 283–286</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> K.H. Chew, "Total chromatic number of graphs of high maximum degree" ''J. Combin. Math. Combin. Comput.'' , '''18''' (1995) pp. 245–254</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A.G. Chetwynd, A.J.W. Hilton, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004072.png" />-factorizing regular graphs of high degree: an improved bound" ''Discrete Math.'' , '''75''' (1989) pp. 103–112</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> S.A. Choudom, "Chromatic bound for a class of graphs" ''Quart. J. Math.'' , '''28''' (1977) pp. 257–270</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> P. Erdös, R.J. Wilson, "On the chromatic index of almost all graphs" ''J. Combin. Th.'' , '''23 B''' (1977) pp. 255–257</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> M.K. Goldberg, "Edge-coloring of multigraphs: recoloring technique" ''J. Graph Theory'' , '''8''' (1984) pp. 123–137</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> A.J.W. Hilton, H.R. Hind, "The total chromatic number of graphs having large maximum degree" ''Discrete Math.'' , '''117''' (1993) pp. 127–140</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> I. Holyer, "The NP-completeness of edge-coloring" ''SIAM J. Comput.'' , '''10''' (1981) pp. 718–720</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> D. König, "Über Graphen und ihre Anwendung auf Determinantentheorie und Mengenlehre" ''Math. Ann.'' , '''77''' (1916) pp. 453–465</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> A.V. Kostochka, "List edge chromatic number of graphs with large girth" ''Discrete Math.'' , '''101''' (1992) pp. 189–201</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> T. Niessen, L. Volkmann, "Class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004073.png" /> conditions depending on the minimum degree and the number of vertices of maximum degree" ''J. Graph Theory'' , '''14''' (1990) pp. 225–246</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> H. Randerath, "The Vizing bound for the chromatic number based on forbidden pairs" ''Doctoral Thesis RWTH Aachen'' (1998)</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> C.E. Shannon, "A theorem on coloring the lines of a network" ''J. Math. Phys.'' , '''28''' (1949) pp. 148–151</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> P.G. Tait, "On the colouring of maps" ''Proc. R. Soc. Edinburgh'' , '''10''' (1880) pp. 501–503; 729</TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> V.G. Vizing, "On an estimate of the chromatic class of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004074.png" />-graph" ''Diskret. Anal.'' , '''3''' (1964) pp. 25–30 (In Russian)</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> V.G. Vizing, "Critical graphs with a given chromatic class" ''Diskret. Anal.'' , '''5''' (1965) pp. 9–17 (In Russian)</TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> V.G. Vizing, "Vertex colouring with given colours" ''Diskret. Anal.'' , '''29''' (1976) pp. 3–10 (In Russian)</TD></TR><TR><TD valign="top">[a22]</TD> <TD valign="top"> L. Volkmann, "Fundamente der Graphentheorie" , Springer (1996)</TD></TR><TR><TD valign="top">[a23]</TD> <TD valign="top"> H.P. Yap, "Total colourings of graphs" , ''Lecture Notes Math.'' , '''1623''' , Springer (1996)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> F. Galvin, "The list chromatic index of a bipartite multigraph" ''J. Combin. Th. B'' , '''68''' (1995) pp. 153–158</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Molloy, B. Reed, "A bound on the total chromatic number" ''Combinatorica'' , '''18''' (1998) pp. 241–280</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Behzad, "Graphs and their chromatic numbers" ''Doctoral Thesis Michigan State Univ.'' (1965)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> L.W. Beineke, "Derived graphs and digraphs" , ''Beiträge zur Graphentheorie'' , Teubner (1968) pp. 17–33</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> K.H. Chew, "On Vizing's theorem, adjacency lemma and fan argument generalized to multigraphs" ''Discrete Math.'' , '''171''' (1997) pp. 283–286</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> K.H. Chew, "Total chromatic number of graphs of high maximum degree" ''J. Combin. Math. Combin. Comput.'' , '''18''' (1995) pp. 245–254</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A.G. Chetwynd, A.J.W. Hilton, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004072.png" />-factorizing regular graphs of high degree: an improved bound" ''Discrete Math.'' , '''75''' (1989) pp. 103–112</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> S.A. Choudom, "Chromatic bound for a class of graphs" ''Quart. J. Math.'' , '''28''' (1977) pp. 257–270</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> P. Erdös, R.J. Wilson, "On the chromatic index of almost all graphs" ''J. Combin. Th.'' , '''23 B''' (1977) pp. 255–257</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> M.K. Goldberg, "Edge-coloring of multigraphs: recoloring technique" ''J. Graph Theory'' , '''8''' (1984) pp. 123–137</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> A.J.W. Hilton, H.R. Hind, "The total chromatic number of graphs having large maximum degree" ''Discrete Math.'' , '''117''' (1993) pp. 127–140</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> I. Holyer, "The NP-completeness of edge-coloring" ''SIAM J. Comput.'' , '''10''' (1981) pp. 718–720</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> D. König, "Über Graphen und ihre Anwendung auf Determinantentheorie und Mengenlehre" ''Math. Ann.'' , '''77''' (1916) pp. 453–465</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> A.V. Kostochka, "List edge chromatic number of graphs with large girth" ''Discrete Math.'' , '''101''' (1992) pp. 189–201</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> T. Niessen, L. Volkmann, "Class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004073.png" /> conditions depending on the minimum degree and the number of vertices of maximum degree" ''J. Graph Theory'' , '''14''' (1990) pp. 225–246</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> H. Randerath, "The Vizing bound for the chromatic number based on forbidden pairs" ''Doctoral Thesis RWTH Aachen'' (1998)</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> C.E. Shannon, "A theorem on coloring the lines of a network" ''J. Math. Phys.'' , '''28''' (1949) pp. 148–151</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> P.G. Tait, "On the colouring of maps" ''Proc. R. Soc. Edinburgh'' , '''10''' (1880) pp. 501–503; 729</TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> V.G. Vizing, "On an estimate of the chromatic class of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v120/v120040/v12004074.png" />-graph" ''Diskret. Anal.'' , '''3''' (1964) pp. 25–30 (In Russian)</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> V.G. Vizing, "Critical graphs with a given chromatic class" ''Diskret. Anal.'' , '''5''' (1965) pp. 9–17 (In Russian)</TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> V.G. Vizing, "Vertex colouring with given colours" ''Diskret. Anal.'' , '''29''' (1976) pp. 3–10 (In Russian)</TD></TR><TR><TD valign="top">[a22]</TD> <TD valign="top"> L. Volkmann, "Fundamente der Graphentheorie" , Springer (1996)</TD></TR><TR><TD valign="top">[a23]</TD> <TD valign="top"> H.P. Yap, "Total colourings of graphs" , ''Lecture Notes Math.'' , '''1623''' , Springer (1996)</TD></TR></table> | ||
Revision as of 14:48, 10 January 2016
Let  be a graph (assumed to be finite, undirected and loop-less), and let
be a graph (assumed to be finite, undirected and loop-less), and let  be the maximum number of edges joining every pair of vertices. A simple graph will mean a graph without parallel edges. The chromatic index
be the maximum number of edges joining every pair of vertices. A simple graph will mean a graph without parallel edges. The chromatic index  is the least number of colours needed to colour the edges of
is the least number of colours needed to colour the edges of  in such a way that no two adjacent edges are assigned the same colour (cf. also Graph colouring). If
in such a way that no two adjacent edges are assigned the same colour (cf. also Graph colouring). If  is the maximum degree of
is the maximum degree of  , then, obviously,
, then, obviously,  . The origins of chromatic graph theory may be traced back to 1852, with the birth of the four-colour problem. The first paper on edge colourings appeared 1880, when P.G. Tait [a18] made the important observation that the four-colour conjecture is equivalent to the statement that every
. The origins of chromatic graph theory may be traced back to 1852, with the birth of the four-colour problem. The first paper on edge colourings appeared 1880, when P.G. Tait [a18] made the important observation that the four-colour conjecture is equivalent to the statement that every  -regular planar graph has chromatic index
-regular planar graph has chromatic index  . But after this, little was done. In 1916, D. König [a13] proved that if
. But after this, little was done. In 1916, D. König [a13] proved that if 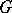 is a bipartite graph (cf. also Graph, bipartite), then
is a bipartite graph (cf. also Graph, bipartite), then 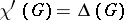 . The first non-trivial upper bound has been obtained by C.E. Shannon [a17] in 1949, when he proved
. The first non-trivial upper bound has been obtained by C.E. Shannon [a17] in 1949, when he proved 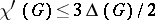 for an arbitrary graph
for an arbitrary graph 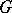 . The great breakthrough occurred in 1964, however, when V.G. Vizing [a19] gave the following surprisingly strong result, now known as Vizing's theorem: If
. The great breakthrough occurred in 1964, however, when V.G. Vizing [a19] gave the following surprisingly strong result, now known as Vizing's theorem: If 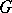 is a graph, then
is a graph, then
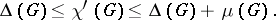 |
In particular, 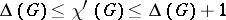 if
if 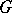 is simple.
is simple.
The cornerstone of Vizing's proof is a brilliant recolouring technique. Up to now (1999) all further proofs of his theorem are based more or less on this method (see, for example, [a5], [a10], and [a22]). In addition, the proof of Vizing's theorem can be used to obtain a polynomial-time algorithm to colour the edges of every graph 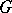 with
with 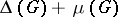 colours. Nowadays, graphs are normally divided into two classes: those with
colours. Nowadays, graphs are normally divided into two classes: those with  are called class-1 graphs, and the others class-2 graphs. Class-2 graphs are relatively scarce, even among the simple graphs [a9]. In view of König's result, bipartite graphs are of class 1; however, the general question whether a given graph is class 1 or class 2 is very difficult, and it is known as the classification problem. This problem is extremely important and has received wide interest. The difficulty of the classification problem lies in the fact that it is
are called class-1 graphs, and the others class-2 graphs. Class-2 graphs are relatively scarce, even among the simple graphs [a9]. In view of König's result, bipartite graphs are of class 1; however, the general question whether a given graph is class 1 or class 2 is very difficult, and it is known as the classification problem. This problem is extremely important and has received wide interest. The difficulty of the classification problem lies in the fact that it is 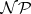 -complete (cf. [a12]; Complexity theory), and that its solution would imply the four-colour theorem. Very little progress has been made for general graphs, and hence it is natural to consider this problem for special families. For regular graphs the so-called one-factorization conjecture goes back to the 1950s: Every simple
-complete (cf. [a12]; Complexity theory), and that its solution would imply the four-colour theorem. Very little progress has been made for general graphs, and hence it is natural to consider this problem for special families. For regular graphs the so-called one-factorization conjecture goes back to the 1950s: Every simple  -regular graph with
-regular graph with 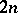 vertices is class 1 (i.e.
vertices is class 1 (i.e. 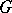 is
is 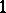 -factorizable) when
-factorizable) when  . This conjecture is still open (1999). The best partial solutions go back to A.G. Chetwynd and A.J.W. Hilton [a7] and T. Niessen and L. Volkmann [a15]. They showed independently that the
. This conjecture is still open (1999). The best partial solutions go back to A.G. Chetwynd and A.J.W. Hilton [a7] and T. Niessen and L. Volkmann [a15]. They showed independently that the 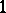 -factorization conjecture is valid if
-factorization conjecture is valid if 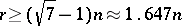 . Appreciable progress has also been achieved in the particular case of planar graphs. On the one hand, if
. Appreciable progress has also been achieved in the particular case of planar graphs. On the one hand, if 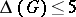 , then a planar graph
, then a planar graph 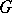 can lie in either class 1 or class 2. On the other hand, Vizing [a20] has proved that every simple planar graph
can lie in either class 1 or class 2. On the other hand, Vizing [a20] has proved that every simple planar graph 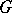 with
with 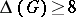 is necessarily of class 1. However, the problem of determining what happens when
is necessarily of class 1. However, the problem of determining what happens when 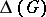 is either
is either 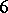 or
or 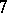 remains open, and has led [a20] to the planar graph conjecture: Every simple planar graph of maximum degree
remains open, and has led [a20] to the planar graph conjecture: Every simple planar graph of maximum degree 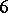 or
or  is of class 1.
is of class 1.
The total chromatic number 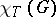 is the least number of colours needed to colour the elements (edges and vertices) of a graph
is the least number of colours needed to colour the elements (edges and vertices) of a graph  so that adjacent elements are coloured differently. The centre of interest lies in the still (1999) unproven total colouring conjecture of Vizing [a20] and M. Behzad [a3] that
so that adjacent elements are coloured differently. The centre of interest lies in the still (1999) unproven total colouring conjecture of Vizing [a20] and M. Behzad [a3] that 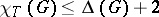 for a simple graph
for a simple graph 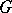 . A.J.W. Hilton and H.R. Hind [a11] proved this conjecture by vertex colouring methods when
. A.J.W. Hilton and H.R. Hind [a11] proved this conjecture by vertex colouring methods when 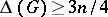 , where
, where  is the number of vertices of
is the number of vertices of  . Also, Vizing's theorem is a powerful tool in attacking this conjecture. For example, K.H. Chew [a6] has given a new proof of the Hilton–Hind result by transforming the total colouring problem to an edge-colouring problem. Using probabilistic methods, recently M. Molloy and B. Reed [a2] have obtained the following very deep theorem: There is an absolute constant
. Also, Vizing's theorem is a powerful tool in attacking this conjecture. For example, K.H. Chew [a6] has given a new proof of the Hilton–Hind result by transforming the total colouring problem to an edge-colouring problem. Using probabilistic methods, recently M. Molloy and B. Reed [a2] have obtained the following very deep theorem: There is an absolute constant 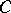 such that
such that 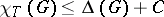 for every simple graph
for every simple graph 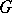 . See [a23] for a thorough treatment of this topic.
. See [a23] for a thorough treatment of this topic.
In order to give reasonable upper bounds for 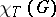 , Vizing [a21] introduced the concept of list colouring: If
, Vizing [a21] introduced the concept of list colouring: If 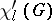 is the list-chromatic index of a graph
is the list-chromatic index of a graph 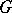 , then, obviously,
, then, obviously,  . Vizing [a21] even posed the still open (1999) list colouring conjecture: Every graph
. Vizing [a21] even posed the still open (1999) list colouring conjecture: Every graph 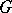 satisfies
satisfies 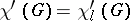 . With a surprisingly short proof, F. Galvin [a1] showed that the list colouring conjecture is true for bipartite graphs. A.V. Kostochka [a14] proved that if all cycles in a simple graph
. With a surprisingly short proof, F. Galvin [a1] showed that the list colouring conjecture is true for bipartite graphs. A.V. Kostochka [a14] proved that if all cycles in a simple graph 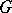 are sufficiently long relative to
are sufficiently long relative to  , then
, then  . If the list colouring conjecture is true, then, according to Vizing's theorem, the same bound would hold for any simple graph.
. If the list colouring conjecture is true, then, according to Vizing's theorem, the same bound would hold for any simple graph.
The determination of the chromatic index can be transformed into a problem dealing with the chromatic number  . Namely, from the definition it is immediate that
. Namely, from the definition it is immediate that 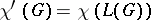 , where
, where 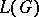 is the line graph of the simple graph
is the line graph of the simple graph 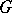 . If, in addition,
. If, in addition, 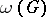 is the clique number (cf. also Fixed-point property) of
is the clique number (cf. also Fixed-point property) of 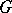 , then Vizing's theorem implies
, then Vizing's theorem implies
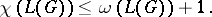 |
Therefore, this bound is called [a16] the Vizing bound. L.W. Beineke [a4] characterized line graphs by nine forbidden induced subgraphs. Using only four forbidden induced subgraphs of Beineke's nine graphs, S.A. Choudom [a8] determined two superclasses of line graphs for which the Vizing bound is also valid. Thus, since 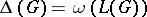 if
if  is not a triangle, Choudom's result extends Vizing's theorem. The most general contribution in this area was found by H. Randerath [a16]: If
is not a triangle, Choudom's result extends Vizing's theorem. The most general contribution in this area was found by H. Randerath [a16]: If  is a simple graph containing neither a complete
is a simple graph containing neither a complete  -graph with an edge missing nor a claw
-graph with an edge missing nor a claw 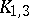 with one subdivided edge as an induced subgraph, then
with one subdivided edge as an induced subgraph, then 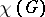 is equal to
is equal to 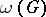 or
or  .
.
References
| [a1] | F. Galvin, "The list chromatic index of a bipartite multigraph" J. Combin. Th. B , 68 (1995) pp. 153–158 |
| [a2] | M. Molloy, B. Reed, "A bound on the total chromatic number" Combinatorica , 18 (1998) pp. 241–280 |
| [a3] | M. Behzad, "Graphs and their chromatic numbers" Doctoral Thesis Michigan State Univ. (1965) |
| [a4] | L.W. Beineke, "Derived graphs and digraphs" , Beiträge zur Graphentheorie , Teubner (1968) pp. 17–33 |
| [a5] | K.H. Chew, "On Vizing's theorem, adjacency lemma and fan argument generalized to multigraphs" Discrete Math. , 171 (1997) pp. 283–286 |
| [a6] | K.H. Chew, "Total chromatic number of graphs of high maximum degree" J. Combin. Math. Combin. Comput. , 18 (1995) pp. 245–254 |
| [a7] | A.G. Chetwynd, A.J.W. Hilton, "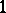 -factorizing regular graphs of high degree: an improved bound" Discrete Math. , 75 (1989) pp. 103–112 -factorizing regular graphs of high degree: an improved bound" Discrete Math. , 75 (1989) pp. 103–112 |
| [a8] | S.A. Choudom, "Chromatic bound for a class of graphs" Quart. J. Math. , 28 (1977) pp. 257–270 |
| [a9] | P. Erdös, R.J. Wilson, "On the chromatic index of almost all graphs" J. Combin. Th. , 23 B (1977) pp. 255–257 |
| [a10] | M.K. Goldberg, "Edge-coloring of multigraphs: recoloring technique" J. Graph Theory , 8 (1984) pp. 123–137 |
| [a11] | A.J.W. Hilton, H.R. Hind, "The total chromatic number of graphs having large maximum degree" Discrete Math. , 117 (1993) pp. 127–140 |
| [a12] | I. Holyer, "The NP-completeness of edge-coloring" SIAM J. Comput. , 10 (1981) pp. 718–720 |
| [a13] | D. König, "Über Graphen und ihre Anwendung auf Determinantentheorie und Mengenlehre" Math. Ann. , 77 (1916) pp. 453–465 |
| [a14] | A.V. Kostochka, "List edge chromatic number of graphs with large girth" Discrete Math. , 101 (1992) pp. 189–201 |
| [a15] | T. Niessen, L. Volkmann, "Class 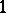 conditions depending on the minimum degree and the number of vertices of maximum degree" J. Graph Theory , 14 (1990) pp. 225–246 conditions depending on the minimum degree and the number of vertices of maximum degree" J. Graph Theory , 14 (1990) pp. 225–246 |
| [a16] | H. Randerath, "The Vizing bound for the chromatic number based on forbidden pairs" Doctoral Thesis RWTH Aachen (1998) |
| [a17] | C.E. Shannon, "A theorem on coloring the lines of a network" J. Math. Phys. , 28 (1949) pp. 148–151 |
| [a18] | P.G. Tait, "On the colouring of maps" Proc. R. Soc. Edinburgh , 10 (1880) pp. 501–503; 729 |
| [a19] | V.G. Vizing, "On an estimate of the chromatic class of a 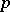 -graph" Diskret. Anal. , 3 (1964) pp. 25–30 (In Russian) -graph" Diskret. Anal. , 3 (1964) pp. 25–30 (In Russian) |
| [a20] | V.G. Vizing, "Critical graphs with a given chromatic class" Diskret. Anal. , 5 (1965) pp. 9–17 (In Russian) |
| [a21] | V.G. Vizing, "Vertex colouring with given colours" Diskret. Anal. , 29 (1976) pp. 3–10 (In Russian) |
| [a22] | L. Volkmann, "Fundamente der Graphentheorie" , Springer (1996) |
| [a23] | H.P. Yap, "Total colourings of graphs" , Lecture Notes Math. , 1623 , Springer (1996) |
Vizing theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vizing_theorem&oldid=37439