Difference between revisions of "Ribaucour curve"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | A planar curve with curvature radius | + | {{TEX|done}} |
| + | A planar curve with curvature radius $R$ at an arbitrary point $M$ proportional to the length of the segment of the normal $MP$ (see Fig.). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r081760a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r081760a.gif" /> | ||
| Line 7: | Line 8: | ||
The equation for the Ribaucour curve in Cartesian orthogonal coordinates is | The equation for the Ribaucour curve in Cartesian orthogonal coordinates is | ||
| − | + | $$x=\int\limits_0^y\frac{dy}{\sqrt{(y/c)^{2n}-1}},$$ | |
| − | where | + | where $n=MP/R$. If $n=1/h$ ($h$ is any integer), then a parametric equation for the Ribaucour curve is |
| − | + | $$x=(m+1)C\int\limits_0^t\sin^{m+1}tdt,\quad y=C\sin^{m+1}t,$$ | |
| − | where | + | where $m=-(n+1)n$. When $m=0$, the Ribaucour curve is a circle; when $m=1$, it is a [[Cycloid|cycloid]]; when $m=-2$, it is a [[Catenary|catenary]]; and when $m=-3$, it is a [[Parabola|parabola]]. |
The length of an arc of the curve is | The length of an arc of the curve is | ||
| − | + | $$l=(m+1)C\int\limits_0^t\sin^mtdt;$$ | |
and the curvature radius is | and the curvature radius is | ||
| − | + | $$R=-(m+1)C\sin^mt.$$ | |
This curve was studied by A. Ribaucour in 1880. | This curve was studied by A. Ribaucour in 1880. | ||
Latest revision as of 20:35, 7 April 2015
A planar curve with curvature radius $R$ at an arbitrary point $M$ proportional to the length of the segment of the normal $MP$ (see Fig.).
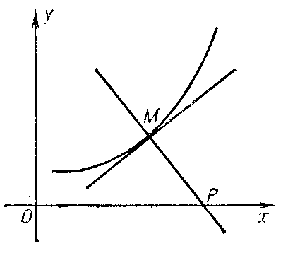
Figure: r081760a
The equation for the Ribaucour curve in Cartesian orthogonal coordinates is
$$x=\int\limits_0^y\frac{dy}{\sqrt{(y/c)^{2n}-1}},$$
where $n=MP/R$. If $n=1/h$ ($h$ is any integer), then a parametric equation for the Ribaucour curve is
$$x=(m+1)C\int\limits_0^t\sin^{m+1}tdt,\quad y=C\sin^{m+1}t,$$
where $m=-(n+1)n$. When $m=0$, the Ribaucour curve is a circle; when $m=1$, it is a cycloid; when $m=-2$, it is a catenary; and when $m=-3$, it is a parabola.
The length of an arc of the curve is
$$l=(m+1)C\int\limits_0^t\sin^mtdt;$$
and the curvature radius is
$$R=-(m+1)C\sin^mt.$$
This curve was studied by A. Ribaucour in 1880.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [2] | P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian) |
Comments
References
| [a1] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
Ribaucour curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ribaucour_curve&oldid=36400