Difference between revisions of "Cantor theorem"
m (→Comments: link) |
m (link) |
||
| Line 11: | Line 11: | ||
Every set of real numbers is the union of the perfect set of its condensation points (cf. [[Condensation point of a set|Condensation point of a set]]) and a countable set. This sometimes called the Cantor–Bendixson theorem. It generalizes to the case of a subset of a metric space with a countable basis (Lindelöf theorem, see , , , , , ). | Every set of real numbers is the union of the perfect set of its condensation points (cf. [[Condensation point of a set|Condensation point of a set]]) and a countable set. This sometimes called the Cantor–Bendixson theorem. It generalizes to the case of a subset of a metric space with a countable basis (Lindelöf theorem, see , , , , , ). | ||
| − | If each of two sets is equipotent to a subset of the other, then these two sets are equipotent. A similar statement holds for two well-ordered sets. This is sometimes called the Cantor–Bernstein theorem or simply Bernstein's theorem (F. Bernshtein gave a correct proof of this theorem, see , , , , , ). | + | If each of two sets is equipotent to a subset of the other, then these two sets are equipotent. A similar statement holds for two well-ordered sets. This is sometimes called the [[Cantor–Bernstein theorem]] or simply Bernstein's theorem (F. Bernshtein gave a correct proof of this theorem, see , , , , , ). |
If | If | ||
Revision as of 19:40, 10 January 2015
The set 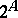 of all subsets of a set
of all subsets of a set 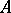 is not equipotent to
is not equipotent to 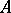 or to any subset of it. The idea behind the proof of this theorem, due to G. Cantor (1878), is called "Cantor diagonalization process03E2003ExxCantor's diagonalization process" and plays a significant role in set theory (and elsewhere). Cantor's theorem implies that no two of the sets
or to any subset of it. The idea behind the proof of this theorem, due to G. Cantor (1878), is called "Cantor diagonalization process03E2003ExxCantor's diagonalization process" and plays a significant role in set theory (and elsewhere). Cantor's theorem implies that no two of the sets
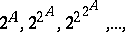 |
are equipotent. In this way one obtains infinitely many distinct cardinal numbers (cf. Cardinal number). Cantor's theorem also implies that the set of all sets does not exist. This means that one must not include among the axioms of set theory the assertion that for each propositional function (or predicate) 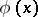 there exists a set consisting of all elements
there exists a set consisting of all elements  satisfying
satisfying 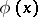 (see , , , ).
(see , , , ).
B.A. Efimov
Any decreasing sequence of non-empty bounded closed sets of real numbers has a non-empty intersection. This generalizes to compact subsets of a metric space. The property: If the diameters of a decreasing sequence of non-empty closed sets in a metric space 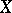 tend to zero then the sets have non-empty intersection, is one of the definitions of completeness of
tend to zero then the sets have non-empty intersection, is one of the definitions of completeness of 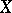 . The property that every totally ordered decreasing family of non-empty closed sets of a topological space
. The property that every totally ordered decreasing family of non-empty closed sets of a topological space 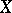 has a non-empty intersection, is one of the definitions of compactness of
has a non-empty intersection, is one of the definitions of compactness of  (see , , , , ).
(see , , , , ).
Every set of real numbers is the union of the perfect set of its condensation points (cf. Condensation point of a set) and a countable set. This sometimes called the Cantor–Bendixson theorem. It generalizes to the case of a subset of a metric space with a countable basis (Lindelöf theorem, see , , , , , ).
If each of two sets is equipotent to a subset of the other, then these two sets are equipotent. A similar statement holds for two well-ordered sets. This is sometimes called the Cantor–Bernstein theorem or simply Bernstein's theorem (F. Bernshtein gave a correct proof of this theorem, see , , , , , ).
If
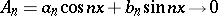 |
for all but a finite number of points of interval 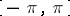 , then
, then 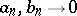 . This generalizes to the case when
. This generalizes to the case when 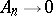 on a set of positive measure (Lebesgue's theorem), when
on a set of positive measure (Lebesgue's theorem), when 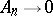 on a set of the second category (Young's theorem), as well as to other situations. Important corollaries are various theorems on sets of uniqueness of trigonometric series (see , , , , , ).
on a set of the second category (Young's theorem), as well as to other situations. Important corollaries are various theorems on sets of uniqueness of trigonometric series (see , , , , , ).
A continuous function on a closed bounded interval of the real line is uniformly continuous on it. This generalizes to continuous mappings from a compact space to a uniform space. This is sometimes called the Heine–Cantor theorem (see [1], [4], [5], [13]).
References
| [1] | G. Cantor, E. Zermelo (ed.) , Gesammelte Abhandlungen , Springer (1932) |
| [2] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [3] | K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968) |
| [4] | P.S. Aleksandrov, "Einführung in die Mengenlehre und in die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
| [5] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
| [6] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [7] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 |
| [8] | G. Cantor, "Ein Beitrag zur Mannigfaltigkeitslehre" J. Reine Angew. Math. , 84 (1878) pp. 242–258 |
| [9] | G. Cantor, "Über trigonometrische Reihen" Math. Ann. , 4 (1871) pp. 139–143 |
| [10] | G. Cantor, "Beiträge zur Begründung des transfiniten Mengenlehre" Math. Ann. , 49 (1897) pp. 207–246 |
| [11] | G. Cantor, "Über unendliche lineare Punktmannigfaltigkeiten" Math. Ann. , 17 (1880) pp. 355–358 |
| [12] | E. Borel, "Leçons sur la théorie des fonctions" , Gauthier-Villars (1928) |
| [13] | E. Heine, "Die Elemente der Funktionenlehre" J. Reine Angew. Math. , 74 (1872) pp. 172–188 |
| [14] | E. Lindelöf, "Remarque sur une théorème fondamental de la théorie des ensembles" Acta Math. , 29 (1905) pp. 183–190 |
| [15a] | G. Cantor, "Über eine die trigonometrischen Reihen betreffenden Lehrsatz" J. Reine Angew. Math. , 72 (1870) pp. 130–138 |
| [15b] | G. Cantor, "Beweis, dass eine für jeden reellen Wert von  durch eine trigonometrische Reihe gegebene Funktion durch eine trigonometrische Reihe gegebene Funktion 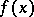 sich nur auf eine einzige Weise in dieser Form darstellen lässt" J. Reine Angew. Math. , 72 (1870) pp. 139–142 sich nur auf eine einzige Weise in dieser Form darstellen lässt" J. Reine Angew. Math. , 72 (1870) pp. 139–142 |
| [16] | G. Cantor, "Über unendliche lineare Punktmannigfaltigkeiten" Math. Ann. , 21 (1883) pp. 51–58 |
| [17] | L. Bendixson, "Quelques théorèmes de la théorie des ensembles de points" Acta Math. , 2 (1883) pp. 415–429 |
| [18] | H. Lebesgue, "Leçons sur les séries trigonométriques" , Gauthier-Villars (1906) |
| [19] | W.H. Young, Proc. Roy. Soc. , 87 (1912) pp. 331–339 |
| [20] | N. Bourbaki, "Eléments d'histoire des mathématiques" , Hermann (1960) |
M.I. Voitsekhovskii
Comments
1) Two sets are equipotent (equivalent) if there is a bijection (a one-to-one onto mapping) between them. Intuitively this means that they have the same number of elements; in other words: They have (or are of) the same cardinality. Cantor's proof is as follows: Assume 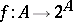 is a mapping; to show that it is not onto, consider
is a mapping; to show that it is not onto, consider 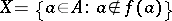 . Then
. Then 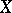 is not in the range of
is not in the range of 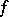 .
.
In an analogous way he showed that the set of real numbers is not countable: Assume 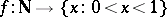 is a mapping and write
is a mapping and write 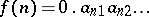 in decimal expansion. Define
in decimal expansion. Define 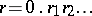 by
by 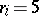 if
if 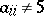 and
and 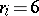 if
if 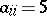 . Then
. Then  is not in the range of
is not in the range of 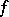 . This last proof best explains the name "diagonalization processdiagonalization process" or "diagonal argumentdiagonal argument" .
. This last proof best explains the name "diagonalization processdiagonalization process" or "diagonal argumentdiagonal argument" .
4) This theorem is also called the Schroeder–Bernstein theorem. A similar statement does not hold for totally ordered sets, consider 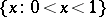 and
and 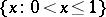 .
.
For general historical information see [20]. For set of the second category cf. Category of a set.
Cantor theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cantor_theorem&oldid=36213