Shnirel'man method

A method for adding sequences of positive integers; created by L.G. Shnirel'man in 1930. Let 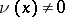be the number of elements of the sequence not larger than . Similarly to the measure of a set, one defines

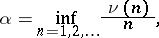the density of the sequence. A sequence 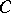the elements of which are 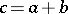, , 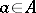, is called the sum of the two sequences 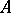and .

Shnirel'man's theorem 1): If 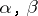are the densities of the summands, then the density of the sum is 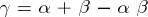. If after adding a sequence to itself a finite number of times one obtains the entire natural series, then the initial sequence is called a basis. In this case every natural number can be represented as the sum of a limited number of summands of the given sequence. A sequence with positive density is a basis.

Shnirel'man's theorem 2): The sequence 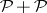has positive density, where the sequence 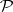consists of the number one and all prime numbers; hence, 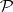is a basis of the natural series, i.e. every natural number 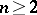can be represented as the sum of a limited number of prime numbers. For the number of summands (Shnirel'man's absolute constant) the estimate 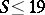has been obtained. In the case of representing a sufficiently large number 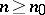by a sum of prime numbers with number of summands 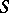(Shnirel'man's constant), Shnirel'man's method together with analytical methods gives 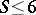. However, by the more powerful method of trigonometric sums of I.M. Vinogradov (cf. Trigonometric sums, method of) the estimate 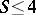was obtained.

Shnirel'man's method was applied to prove that the sequence consisting of the number one and of the numbers of the form 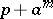, where 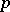is a prime number, 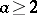is a natural number and is a basis of the natural series (N.P. Romanov, 1934).

References

[1]	L.G. [L.G. Shnirel'man] Schnirelmann, "Ueber additive Eigenschaften von Zahlen" Math. Ann. , 107 (1933) pp. 649–690
[2]	A.Ya. Khinchin, "Three pearls of number theory" , Graylock (1952) Translation from the second, revised Russian ed. [1948] Zbl 0048.27202 Reprinted Dover (2003) ISBN 0486400263
[3]	K. Prachar, "Primzahlverteilung" , Springer (1957)