Newton interpolation formula

A form of writing the Lagrange interpolation formula by using divided differences:

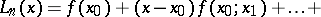(1)

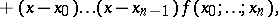where 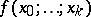are the divided differences of order 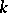; it was treated by I. Newton in 1687. Formula (1) is called Newton's interpolation formula for unequal differences. When the 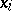are equidistant, that is, if

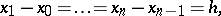then by introducing the notation 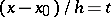and expressing the divided differences 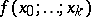in terms of the finite differences 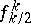according to the formula

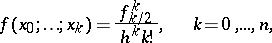one obtains a way of writing the polynomial 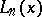in the form

(2)

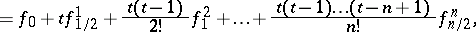which is called Newton's interpolation formula for forward interpolation. If the same change of variables is made in the interpolation polynomial 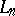with nodes 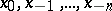, where ,

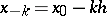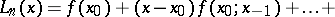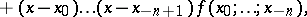then one obtains Newton's interpolation formula for backward interpolation:

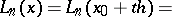(3)

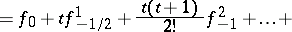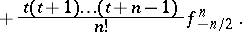Formulas (2) and (3) are convenient for computing tables of a given function 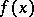if the point is at the beginning or the end of the table, since in this case the addition of one or several nodes caused by the wish to increase the accuracy of the approximation does not lead to a repetition of the whole work done as in computations with Lagrange's formula.

References

[1]	I.S. Berezin, N.P. Zhidkov, "Computing methods" , 1 , Pergamon (1973) (Translated from Russian)
[2]	N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)

Comments

The divided differences 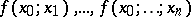are defined by:

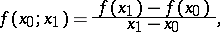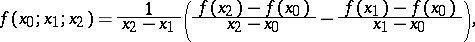or

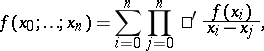where the prime in 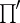means that the factor 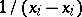is to be omitted. Formula (1) is also known as the finite Newton series for a function .

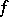References

[a1]	K.E. Atkinson, "An introduction to numerical analysis" , Wiley (1978)
[a2]	P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975)
[a3]	F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1974)