Difference between revisions of "Aitken scheme"
From Encyclopedia of Mathematics
(Importing text file) |
m (links) |
||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011220/a0112205.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011220/a0112205.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011220/a0112206.png" /> is the interpolation polynomial with interpolation nodes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011220/a0112207.png" />, in particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011220/a0112208.png" /> (see [[ | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011220/a0112206.png" /> is the interpolation polynomial with interpolation nodes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011220/a0112207.png" />, in particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011220/a0112208.png" /> (see [[Interpolation formula]]). The process of computations by means of (*) may finish if the values of two interpolation polynomials of consecutive degrees coincide in the required number of decimal places. The Aitken scheme is convenient for interpolating the values of a function given in the form of a table (of values), by renumbering the interpolation nodes in the order in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011220/a0112209.png" /> increases. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.S. Berezin, N.P. Zhidkov, "Computing methods" , '''1''' , Pergamon (1973) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> I.S. Berezin, N.P. Zhidkov, "Computing methods" , '''1''' , Pergamon (1973) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)</TD></TR> | ||
| + | </table> | ||
====Comments==== | ====Comments==== | ||
| − | Aitken published the gist of his method in [[#References|[a1]]]. Aitken's scheme is disadvantageous when a number of interpolations must be carried out over the same range. In such cases, an alternative to the computation of the Lagrange polynomials is the use of divided | + | Aitken published the gist of his method in [[#References|[a1]]]. Aitken's scheme is disadvantageous when a number of interpolations must be carried out over the same range. In such cases, an alternative to the computation of the Lagrange polynomials is the use of [[divided difference]]s in the construction of [[Newton interpolation formula|Newton's interpolation formula]]. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.C. Aitken, "On interpolation by iteration of proportional parts, without the use of differences" ''Proc. Edingburgh Math. Soc.'' , '''3''' : 2 (1932) pp. 56–76</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1974)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> A.C. Aitken, "On interpolation by iteration of proportional parts, without the use of differences" ''Proc. Edingburgh Math. Soc.'' , '''3''' : 2 (1932) pp. 56–76</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1974)</TD></TR> | ||
| + | </table> | ||
Revision as of 15:38, 3 January 2015
A method for computing the value at a point 
of the interpolation polynomial 
with respect to the nodes 
, based on the successive application of the formula
 | (*) |
 |
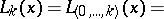where 
is the interpolation polynomial with interpolation nodes 
, in particular, 
(see Interpolation formula). The process of computations by means of (*) may finish if the values of two interpolation polynomials of consecutive degrees coincide in the required number of decimal places. The Aitken scheme is convenient for interpolating the values of a function given in the form of a table (of values), by renumbering the interpolation nodes in the order in which 
increases.
References
| [1] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , 1 , Pergamon (1973) (Translated from Russian) |
| [2] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
Comments
Aitken published the gist of his method in [a1]. Aitken's scheme is disadvantageous when a number of interpolations must be carried out over the same range. In such cases, an alternative to the computation of the Lagrange polynomials is the use of divided differences in the construction of Newton's interpolation formula.
References
| [a1] | A.C. Aitken, "On interpolation by iteration of proportional parts, without the use of differences" Proc. Edingburgh Math. Soc. , 3 : 2 (1932) pp. 56–76 |
| [a2] | F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1974) |
How to Cite This Entry:
Aitken scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Aitken_scheme&oldid=36049
Aitken scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Aitken_scheme&oldid=36049
This article was adapted from an original article by M.K. Samarin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article