|
|
| Line 70: |
Line 70: |
| | | | |
| | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004032.png" /> denotes the familiar [[Riemann zeta-function|Riemann zeta-function]]. | | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004032.png" /> denotes the familiar [[Riemann zeta-function|Riemann zeta-function]]. |
| − |
| |
| − | ==Euler–Mascheroni constant.==
| |
| − | Another important mathematical constant is the Euler–Mascheroni constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004033.png" /> (which is denoted also by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004034.png" />), defined by
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004035.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a12)</td></tr></table>
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004036.png" /></td> </tr></table>
| |
| − |
| |
| − | It is named after L. Euler (1707–1783) and L. Mascheroni (1750–1800). Indeed, one also has
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004037.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a13)</td></tr></table>
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004038.png" /></td> </tr></table>
| |
| − |
| |
| − | and
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004039.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a14)</td></tr></table>
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004040.png" /></td> </tr></table>
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004041.png" /></td> </tr></table>
| |
| − |
| |
| − | where an empty sum is interpreted, as usual, to be zero. In terms of the Riemann zeta-function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004042.png" />, Euler's classical results state:
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004043.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a15)</td></tr></table>
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004044.png" /></td> </tr></table>
| |
| − |
| |
| − | ====References====
| |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Erdélyi, W. Magnus, F. Oberhettinger, F.G. Tricomi, "Higher transcendental functions" , '''I''' , McGraw-Hill (1953)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Lewin, "Polylogarithms and associated functions" , Elsevier (1981)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H.M. Srivastava, J. Choi, "Series associated with the zeta and related functions" , Kluwer Acad. Publ. (2001)</TD></TR></table>
| |
Revision as of 19:07, 29 December 2014
Named after its inventor, E.Ch. Catalan (1814–1894), the Catalan constant 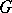 (which is denoted also by
(which is denoted also by 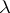 ) is defined by
) is defined by
 | (a1) |
If, in terms of the Digamma (or Psi) function 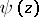 , defined by
, defined by
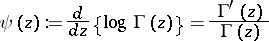 | (a2) |
or
one puts
 | (a3) |
where
then
 | (a4) |
which provides a relationship between the Catalan constant 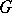 and the Digamma function
and the Digamma function 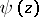 .
.
The Catalan constant 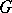 is related also to other functions, such as the Clausen function
is related also to other functions, such as the Clausen function 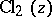 , defined by
, defined by
 | (a5) |
and the Hurwitz zeta-function 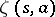 , which is defined, when
, which is defined, when 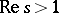 , by
, by
 | (a6) |
Thus,
 | (a7) |
Since
 | (a8) |
the last expression in (a7) would follow also from (a4) in light of the definition in (a3).
A fairly large number of integrals and series can be evaluated in terms of the Catalan constant 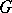 . For example,
. For example,
 | (a9) |
 | (a10) |
and
 | (a11) |
where 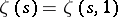 denotes the familiar Riemann zeta-function.
denotes the familiar Riemann zeta-function.
How to Cite This Entry:
Catalan constant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Catalan_constant&oldid=35952
This article was adapted from an original article by Hari M. Srivastava (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article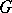 (which is denoted also by
(which is denoted also by 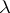 ) is defined by
) is defined by

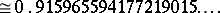
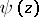 , defined by
, defined by
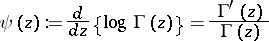
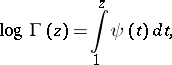

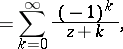
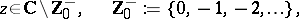

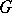 and the Digamma function
and the Digamma function 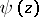 .
.
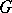 is related also to other functions, such as the Clausen function
is related also to other functions, such as the Clausen function 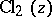 , defined by
, defined by

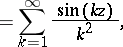
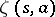 , which is defined, when
, which is defined, when 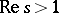 , by
, by

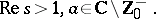

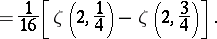

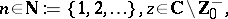
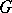 . For example,
. For example,

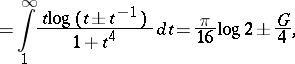

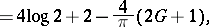

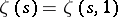 denotes the familiar Riemann zeta-function.
denotes the familiar Riemann zeta-function.