Difference between revisions of "Free semi-group"
(Importing text file) |
m (link) |
||
| Line 3: | Line 3: | ||
The semi-group whose elements are all possible finite sequences of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416402.png" /> (letters), and the operation consists of placing one sequence after another. The elements of a free semi-group are usually called words (cf. [[Word|Word]]), and the operation is often called concatenation. For the sake of convenience, the empty word 1 is often adjoined (its length is, by definition, zero) by setting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416403.png" /> for any word <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416404.png" />; the semi-group with an identity that arises in this way is called the free monoid over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416405.png" />. The free semi-group (respectively, free monoid) over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416406.png" /> is often denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416407.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416408.png" />). The alphabet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416409.png" /> for the free semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164010.png" /> is the unique irreducible generating set that consists of just those elements that cannot be decomposed into products. The letters of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164011.png" /> are called free generators. A free semi-group is defined uniquely up to an isomorphism by the cardinality of its alphabet, called the rank of the free semi-group. The free semi-group of rank 2 has sub-semi-groups that are free of countable rank. | The semi-group whose elements are all possible finite sequences of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416402.png" /> (letters), and the operation consists of placing one sequence after another. The elements of a free semi-group are usually called words (cf. [[Word|Word]]), and the operation is often called concatenation. For the sake of convenience, the empty word 1 is often adjoined (its length is, by definition, zero) by setting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416403.png" /> for any word <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416404.png" />; the semi-group with an identity that arises in this way is called the free monoid over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416405.png" />. The free semi-group (respectively, free monoid) over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416406.png" /> is often denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416407.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416408.png" />). The alphabet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f0416409.png" /> for the free semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164010.png" /> is the unique irreducible generating set that consists of just those elements that cannot be decomposed into products. The letters of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164011.png" /> are called free generators. A free semi-group is defined uniquely up to an isomorphism by the cardinality of its alphabet, called the rank of the free semi-group. The free semi-group of rank 2 has sub-semi-groups that are free of countable rank. | ||
| − | Free semi-groups are the free objects (cf. [[Free algebra|Free algebra]]) in the category of all semi-groups. For a semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164012.png" /> the following conditions are equivalent: 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164013.png" /> is free; 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164014.png" /> has a generating set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164015.png" /> such that any element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164016.png" /> can be uniquely represented as a product of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164017.png" />; and 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164018.png" /> satisfies the cancellation law, does not contain idempotents, every element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164019.png" /> has a finite number of divisors, and for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164020.png" /> the equality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164021.png" /> implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164022.png" />, or that one of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164023.png" /> is a left divisor of the other. | + | Free semi-groups are the free objects (cf. [[Free algebra|Free algebra]]) in the category of all semi-groups. For a semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164012.png" /> the following conditions are equivalent: 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164013.png" /> is free; 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164014.png" /> has a generating set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164015.png" /> such that any element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164016.png" /> can be uniquely represented as a product of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164017.png" />; and 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164018.png" /> satisfies the [[cancellation law]], does not contain idempotents, every element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164019.png" /> has a finite number of divisors, and for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164020.png" /> the equality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164021.png" /> implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164022.png" />, or that one of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164023.png" /> is a left divisor of the other. |
Every sub-semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164024.png" /> of a free semi-group has a unique irreducible generating set, which consists of elements that cannot be decomposed into a product in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164025.png" />; however, not every sub-semi-group of a free semi-group is free. The following conditions on a sub-semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164026.png" /> of a free semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164027.png" /> are equivalent: 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164028.png" /> is a free semi-group; 2) for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164029.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164030.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164031.png" /> imply that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164032.png" />; and 3) for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164033.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164034.png" /> implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164035.png" />. For arbitrary different words <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164036.png" /> in a free semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164037.png" />, either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164038.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164039.png" /> are free generators of the sub-semi-group generated by them, or there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164040.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164041.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164042.png" /> for some natural numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164044.png" />; the second alternative holds if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164045.png" />. Every sub-semi-group with three generators in a free semi-group is finitely presented, but there are sub-semi-groups with four generators that are not. | Every sub-semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164024.png" /> of a free semi-group has a unique irreducible generating set, which consists of elements that cannot be decomposed into a product in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164025.png" />; however, not every sub-semi-group of a free semi-group is free. The following conditions on a sub-semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164026.png" /> of a free semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164027.png" /> are equivalent: 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164028.png" /> is a free semi-group; 2) for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164029.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164030.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164031.png" /> imply that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164032.png" />; and 3) for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164033.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164034.png" /> implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164035.png" />. For arbitrary different words <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164036.png" /> in a free semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164037.png" />, either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164038.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164039.png" /> are free generators of the sub-semi-group generated by them, or there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164040.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164041.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164042.png" /> for some natural numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164044.png" />; the second alternative holds if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041640/f04164045.png" />. Every sub-semi-group with three generators in a free semi-group is finitely presented, but there are sub-semi-groups with four generators that are not. | ||
Revision as of 16:18, 21 December 2014
over an alphabet 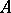
The semi-group whose elements are all possible finite sequences of elements of 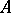 (letters), and the operation consists of placing one sequence after another. The elements of a free semi-group are usually called words (cf. Word), and the operation is often called concatenation. For the sake of convenience, the empty word 1 is often adjoined (its length is, by definition, zero) by setting
(letters), and the operation consists of placing one sequence after another. The elements of a free semi-group are usually called words (cf. Word), and the operation is often called concatenation. For the sake of convenience, the empty word 1 is often adjoined (its length is, by definition, zero) by setting 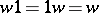 for any word
for any word 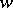 ; the semi-group with an identity that arises in this way is called the free monoid over
; the semi-group with an identity that arises in this way is called the free monoid over 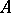 . The free semi-group (respectively, free monoid) over
. The free semi-group (respectively, free monoid) over 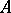 is often denoted by
is often denoted by 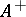 (respectively,
(respectively, 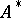 ). The alphabet
). The alphabet  for the free semi-group
for the free semi-group 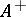 is the unique irreducible generating set that consists of just those elements that cannot be decomposed into products. The letters of
is the unique irreducible generating set that consists of just those elements that cannot be decomposed into products. The letters of 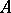 are called free generators. A free semi-group is defined uniquely up to an isomorphism by the cardinality of its alphabet, called the rank of the free semi-group. The free semi-group of rank 2 has sub-semi-groups that are free of countable rank.
are called free generators. A free semi-group is defined uniquely up to an isomorphism by the cardinality of its alphabet, called the rank of the free semi-group. The free semi-group of rank 2 has sub-semi-groups that are free of countable rank.
Free semi-groups are the free objects (cf. Free algebra) in the category of all semi-groups. For a semi-group 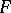 the following conditions are equivalent: 1)
the following conditions are equivalent: 1) 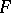 is free; 2)
is free; 2) 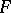 has a generating set
has a generating set 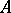 such that any element of
such that any element of 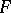 can be uniquely represented as a product of elements of
can be uniquely represented as a product of elements of 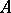 ; and 3)
; and 3) 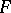 satisfies the cancellation law, does not contain idempotents, every element of
satisfies the cancellation law, does not contain idempotents, every element of 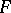 has a finite number of divisors, and for any
has a finite number of divisors, and for any  the equality
the equality  implies that
implies that 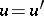 , or that one of
, or that one of 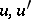 is a left divisor of the other.
is a left divisor of the other.
Every sub-semi-group  of a free semi-group has a unique irreducible generating set, which consists of elements that cannot be decomposed into a product in
of a free semi-group has a unique irreducible generating set, which consists of elements that cannot be decomposed into a product in  ; however, not every sub-semi-group of a free semi-group is free. The following conditions on a sub-semi-group
; however, not every sub-semi-group of a free semi-group is free. The following conditions on a sub-semi-group 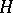 of a free semi-group
of a free semi-group 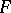 are equivalent: 1)
are equivalent: 1) 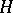 is a free semi-group; 2) for any
is a free semi-group; 2) for any 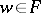 ,
,  and
and 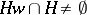 imply that
imply that 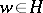 ; and 3) for any
; and 3) for any 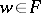 ,
, 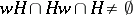 implies that
implies that 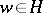 . For arbitrary different words
. For arbitrary different words 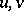 in a free semi-group
in a free semi-group 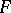 , either
, either  and
and  are free generators of the sub-semi-group generated by them, or there is a
are free generators of the sub-semi-group generated by them, or there is a 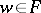 such that
such that 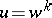 ,
,  for some natural numbers
for some natural numbers 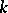 and
and  ; the second alternative holds if and only if
; the second alternative holds if and only if  . Every sub-semi-group with three generators in a free semi-group is finitely presented, but there are sub-semi-groups with four generators that are not.
. Every sub-semi-group with three generators in a free semi-group is finitely presented, but there are sub-semi-groups with four generators that are not.
Free semi-groups arise naturally in the algebraic theory of automata (cf. Automata, algebraic theory of, see also [5], [6]), the theory of coding (see Coding, alphabetical, [4]–[6]), and the theory of formal languages and formal grammars (cf. Grammar, formal, see also [3], [5], [6]). Connected with these topics are the problems of solving equations in free semi-groups (see [7]–[9]). There are algorithms that recognize the solvability of arbitrary equations in a free semi-group.
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [2] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [3] | M. Gross, A. Lentin, "Introduction to formal grammars" , Springer (1970) (Translated from French) |
| [4] | A.A. Markov, "Introduction to coding theory" , Moscow (1982) (In Russian) |
| [5] | S. Eilenberg, "Automata, languages and machines" , A-B , Acad. Press (1974–1976) |
| [6] | G. Lallement, "Semi-groups and combinatorial applications" , Wiley (1979) |
| [7] | A. Lentin, "Equations dans les monoids libres" , Mouton (1972) |
| [8] | Yu.I. Khmelevskii, "Equations in free semi-groups" Proc. Steklov Inst. Math. , 107 (1976) Trudy Mat. Inst. Steklov. , 107 (1971) |
| [9] | G.S. Makanin, "The problem of solvability of equations in a free semigroup" Math. USSR-Sb. , 32 : 2 (1977) pp. 129–198 Mat. Sb. , 103 : 2 (1977) pp. 147–236 |
Comments
The (categorical) freeness property of the free semi-group 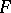 over the set
over the set 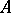 is the following. For every semi-group
is the following. For every semi-group  and mapping of sets
and mapping of sets 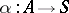 there is a unique homomorphism of semi-groups
there is a unique homomorphism of semi-groups 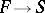 extending
extending 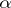 . A similar property holds for the free monoid.
. A similar property holds for the free monoid.
Free semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_semi-group&oldid=35780