Difference between revisions of "Artin-Schreier theory"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Artin–Schreier theory to Artin-Schreier theory: ascii title) |
m (links) |
||
| Line 1: | Line 1: | ||
| − | The phrase "Artin–Schreier theory" usually refers to a chapter in the theory of | + | The phrase "Artin–Schreier theory" usually refers to a chapter in the theory of [[ordered field]]s. |
| − | A field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a1107501.png" /> | + | A [[formally real field]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a1107501.png" /> has the property that the only solutions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a1107502.png" /> are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a1107503.png" />. Any such field can be ordered and, conversely, any ordered field is formally real. A [[real-closed field]] is a formally real field that is maximal under algebraic extensions. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a1107504.png" /> is real closed, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a1107505.png" /> is algebraically closed and, conversely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a1107506.png" /> is algebraically closed and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a1107507.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a1107508.png" /> is real closed (the Artin–Schreier characterization of real-closed fields). A further Artin–Schreier theorem is that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a1107509.png" /> is the algebraic closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075012.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075013.png" /> is real closed and hence of characteristic zero and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075014.png" />. |
The theory of formally real fields led E. Artin to the solution of the Hilbert problem on the resolution of definite rational functions as sums of squares (the Artin theorem): Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075015.png" /> be a field of real numbers, i.e. a subfield of the field of real numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075016.png" />, which has a unique ordering, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075017.png" /> be a rational function (of several variables) with coefficients in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075018.png" /> that is rationally definite in the sense that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075019.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075020.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075021.png" /> is defined. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075022.png" /> is a sum of squares of rational functions with coefficients in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075023.png" />. | The theory of formally real fields led E. Artin to the solution of the Hilbert problem on the resolution of definite rational functions as sums of squares (the Artin theorem): Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075015.png" /> be a field of real numbers, i.e. a subfield of the field of real numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075016.png" />, which has a unique ordering, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075017.png" /> be a rational function (of several variables) with coefficients in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075018.png" /> that is rationally definite in the sense that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075019.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075020.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075021.png" /> is defined. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075022.png" /> is a sum of squares of rational functions with coefficients in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110750/a11075023.png" />. | ||
Revision as of 19:54, 7 December 2014
The phrase "Artin–Schreier theory" usually refers to a chapter in the theory of ordered fields.
A formally real field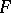 
has the property that the only solutions of 
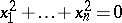are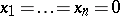 
. Any such field can be ordered and, conversely, any ordered field is formally real. A real-closed field is a formally real field that is maximal under algebraic extensions. If 
is real closed, then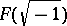 
is algebraically closed and, conversely, if 
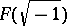is algebraically closed and 
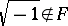, then 
is real closed (the Artin–Schreier characterization of real-closed fields). A further Artin–Schreier theorem is that if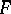 
is the algebraic closure of 
, 
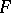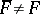and 
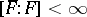, then 
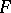is real closed and hence of characteristic zero and 
.
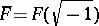The theory of formally real fields led E. Artin to the solution of the Hilbert problem on the resolution of definite rational functions as sums of squares (the Artin theorem): Let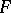 
be a field of real numbers, i.e. a subfield of the field of real numbers 
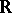, which has a unique ordering, and let 
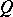be a rational function (of several variables) with coefficients in 
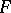that is rationally definite in the sense that 
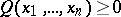for all 
for which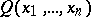 
is defined. Then 
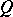is a sum of squares of rational functions with coefficients in 
.
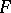References
| [a1] | N. Jacobson, "Lectures in abstract algebra" , III: theory of fields and Galois theory , v. Nostrand (1964) pp. Chapt. VI |
| [a2] | P. Ribenboim, "L'arithmétique des corps" , Hermann (1972) pp. Chapt. IX |
How to Cite This Entry:
Artin-Schreier theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Artin-Schreier_theory&oldid=35475
Artin-Schreier theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Artin-Schreier_theory&oldid=35475
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article