Difference between revisions of "Sperner property"
(Importing text file) |
m (links) |
||
| Line 1: | Line 1: | ||
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304901.png" /> be a finite [[Partially ordered set|partially ordered set]] (abbreviated: poset) which possesses a rank function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304902.png" />, i.e. a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304903.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304904.png" /> for some minimal element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304905.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304906.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304907.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304908.png" /> covers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304909.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049010.png" /> and there is no element between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049012.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049013.png" /> be its <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049014.png" />th level and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049015.png" /> be the rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049016.png" />. | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304901.png" /> be a finite [[Partially ordered set|partially ordered set]] (abbreviated: poset) which possesses a rank function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304902.png" />, i.e. a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304903.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304904.png" /> for some minimal element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304905.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304906.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304907.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304908.png" /> covers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304909.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049010.png" /> and there is no element between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049012.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049013.png" /> be its <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049014.png" />th level and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049015.png" /> be the rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049016.png" />. | ||
| − | An anti-chain or Sperner family in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049017.png" /> is a subset of pairwise incomparable elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049018.png" />. Obviously, each level is an anti-chain. The width | + | An [[anti-chain]] or Sperner family in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049017.png" /> is a subset of pairwise incomparable elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049018.png" />. Obviously, each level is an anti-chain. The [[width of a partially ordered set]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049019.png" /> (Dilworth number or Sperner number) is the maximum size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049020.png" /> of an anti-chain of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049021.png" />. The poset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049022.png" /> is said to have the Sperner property if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049023.png" />. E. Sperner proved in 1928 the Sperner property for Boolean lattices (cf. also [[Sperner theorem|Sperner theorem]]). |
More generally, a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049025.png" />-family, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049026.png" />, is a subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049027.png" /> containing no chain of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049028.png" /> elements in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049029.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049030.png" /> has the strong Sperner property if for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049031.png" /> the largest size of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049032.png" />-family in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049033.png" /> equals the largest size of a union of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049034.png" /> levels. There exist several classes of posets having the strong Sperner property: | More generally, a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049025.png" />-family, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049026.png" />, is a subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049027.png" /> containing no chain of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049028.png" /> elements in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049029.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049030.png" /> has the strong Sperner property if for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049031.png" /> the largest size of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049032.png" />-family in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049033.png" /> equals the largest size of a union of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049034.png" /> levels. There exist several classes of posets having the strong Sperner property: | ||
Revision as of 22:09, 6 December 2014
Let  be a finite partially ordered set (abbreviated: poset) which possesses a rank function
be a finite partially ordered set (abbreviated: poset) which possesses a rank function  , i.e. a function
, i.e. a function  such that
such that 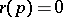 for some minimal element
for some minimal element 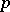 of
of 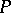 and
and 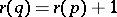 whenever
whenever 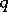 covers
covers 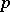 , i.e.
, i.e. 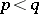 and there is no element between
and there is no element between  and
and 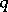 . Let
. Let 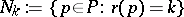 be its
be its 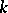 th level and let
th level and let 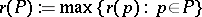 be the rank of
be the rank of 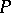 .
.
An anti-chain or Sperner family in 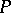 is a subset of pairwise incomparable elements of
is a subset of pairwise incomparable elements of 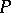 . Obviously, each level is an anti-chain. The width of a partially ordered set
. Obviously, each level is an anti-chain. The width of a partially ordered set 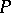 (Dilworth number or Sperner number) is the maximum size
(Dilworth number or Sperner number) is the maximum size 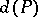 of an anti-chain of
of an anti-chain of 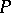 . The poset
. The poset 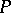 is said to have the Sperner property if
is said to have the Sperner property if 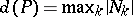 . E. Sperner proved in 1928 the Sperner property for Boolean lattices (cf. also Sperner theorem).
. E. Sperner proved in 1928 the Sperner property for Boolean lattices (cf. also Sperner theorem).
More generally, a  -family,
-family,  , is a subset of
, is a subset of 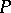 containing no chain of
containing no chain of 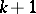 elements in
elements in 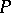 , and
, and 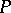 has the strong Sperner property if for each
has the strong Sperner property if for each 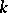 the largest size of a
the largest size of a 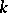 -family in
-family in 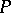 equals the largest size of a union of
equals the largest size of a union of 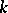 levels. There exist several classes of posets having the strong Sperner property:
levels. There exist several classes of posets having the strong Sperner property:
LYM posets, i.e. posets 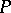 satisfying the LYM inequality (cf. also Sperner theorem)
satisfying the LYM inequality (cf. also Sperner theorem)
 |
for every anti-chain 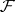 in
in 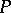 or, equivalently,
or, equivalently,
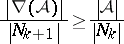 |
for all 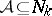 ,
, 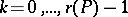 , where
, where 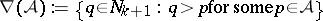 . This equivalent property is called the normalized matching property of
. This equivalent property is called the normalized matching property of 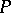 .
.
Symmetric chain orders, i.e. ranked posets 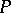 which can be decomposed into chains of the form
which can be decomposed into chains of the form 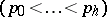 where
where 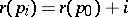 ,
, 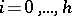 , and
, and 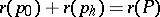 .
.
Peck posets, i.e. ranked posets 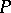 such that
such that  for all
for all 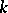 and there is a linear operator
and there is a linear operator  on the vector space having the basis
on the vector space having the basis 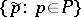 with the following properties:
with the following properties:
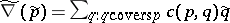 with some numbers
with some numbers 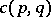 ,
,
the subspace generated by 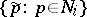 is mapped via
is mapped via 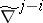 to a subspace of dimension
to a subspace of dimension 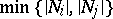 for all
for all 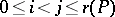 . If
. If 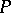 and
and 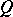 are posets from one class, then also the direct product
are posets from one class, then also the direct product 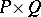 (ordered componentwise) belongs to that class, where in the case of LYM posets an additional condition must be supposed:
(ordered componentwise) belongs to that class, where in the case of LYM posets an additional condition must be supposed: 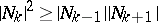 for all
for all 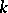 (so-called logarithmic concavity). Moreover, quotient theorems have been proved for LYM posets with weight functions and Peck posets.
(so-called logarithmic concavity). Moreover, quotient theorems have been proved for LYM posets with weight functions and Peck posets.
Every LYM poset with the symmetry and unimodality property 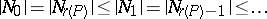 is a symmetric chain order and every symmetric chain order is a Peck poset.
is a symmetric chain order and every symmetric chain order is a Peck poset.
Standard examples of posets belonging to all these three classes are the lattice of subsets of a finite set, ordered by inclusion (the Boolean lattice), the lattice of divisors of a natural number, ordered by divisibility, the lattice of all subspaces of an  -dimensional vector space over a finite field, ordered by inclusion. The poset of faces of an
-dimensional vector space over a finite field, ordered by inclusion. The poset of faces of an  -dimensional cube, ordered by inclusion, belongs only to the class of LYM posets. The lattice of partitions of a finite set, ordered by refinement, even does not have the Sperner property if
-dimensional cube, ordered by inclusion, belongs only to the class of LYM posets. The lattice of partitions of a finite set, ordered by refinement, even does not have the Sperner property if  is sufficiently large.
is sufficiently large.
Details can be found in [a1].
References
| [a1] | K. Engel, "Sperner theory" , Cambridge Univ. Press (1997) |
Sperner property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sperner_property&oldid=35430