Cardinal number

transfinite number, power in the sense of Cantor, cardinality of a set

That property of the set which is intrinsic to any set 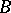with the same cardinality as 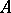. In this connection, two sets and 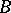are said to have the same cardinality (or to be equivalent) if there is a one-to-one onto function 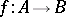with domain of definition 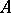and set of values 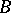. G. Cantor defined the cardinal number of a set as that property of it which remains after abstracting the qualitative nature of its elements and their ordering. By way of stressing the double act of abstraction, Cantor introduced the symbol 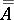to denote the cardinal number of 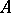. The most commonly used from among the various notations for a cardinal number are the symbols 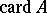and . 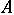If 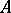is a finite set containing elements, then . 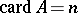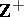If denotes the set of natural numbers, then 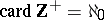(see Aleph). If denotes the set of real numbers, then 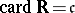, the power of the continuum. The set 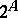of all subsets of 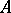is not equivalent to 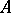or to any subset of 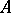(Cantor's theorem). In particular, no two of the sets

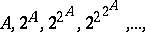(1)

are equivalent. When 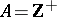, the above sequence gives rise to infinitely many distinct infinite cardinal numbers. Further cardinal numbers are obtained by taking the union 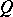of the sets in (1) and constructing the analogous sequence, setting 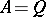. This process can be continued infinitely often. The scale (class) of all infinite cardinal numbers is much richer than the scale (class) of finite cardinals. Furthermore, there are so many of them that it is not possible to form a set containing at least one of each cardinal number.

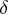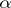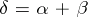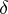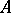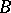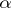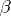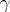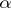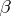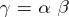One can define for cardinal numbers the operations of addition, multiplication, raising to a power, as well as taking the logarithm and extracting a root. 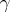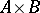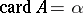Thus, the cardinal number is the sum of and , , if each set of cardinality can be represented as a disjoint union of sets and of cardinalities and , respectively; the cardinal number is the product of and , , if is the cardinal number of the Cartesian product where and 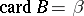. Addition and multiplication of cardinal numbers is commutative and associative, and multiplication is distributive with respect to addition. 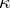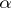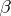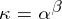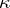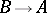The cardinal number is the power with base and exponent , , if every set of cardinality is equivalent to the set of all functions , where 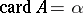and 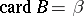. The cardinal number is said to be smaller or equal to the cardinal number 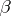, , 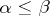if every set of cardinality is equivalent to some subset of a set of cardinality . 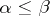If and 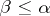, then 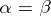(the Cantor–Bernstein theorem), so that the scale of cardinal numbers is totally ordered. Furthermore, for each cardinal number 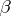the set 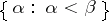is totally well-ordered, which enables one to define the logarithm 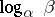of 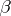to the base 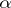, , 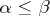as the smallest cardinal number 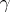such that 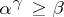; similarly, the 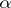-th root 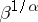of the cardinal number 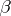is the smallest cardinal number 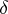such that .

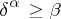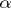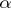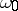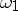Any cardinal number can be identified with the smallest ordinal number of cardinality . In particular, corresponds to the ordinal number , to the ordinal , etc. Thus, the scale of cardinal numbers is a subscale of the scale of ordinal numbers. A number of properties of ordinal numbers carry over to cardinal numbers; however, these same properties can also be defined "intrinsically" . If 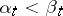for every 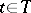and if 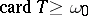, then

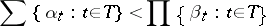(2)

(König's theorem). If in (2) one sets 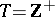and 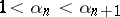, then

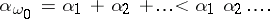(3)

In particular, for any 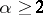it is impossible to express the power 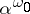as the sum of an infinite increasing sequence of length 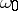all terms of which are less than 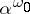. For each cardinal number 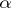, the cofinal character of 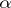, denoted by 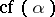, is defined as the smallest cardinal number 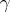such that 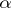can be written as 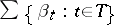for suitable 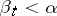and . If 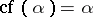, then 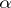is called regular, otherwise it is called singular. For each cardinal number 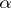, the smallest cardinal number 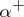greater than 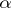is regular (granted the axiom of choice). An example of a singular cardinal number is the cardinal number 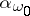on the left-hand side of (3) under the condition that 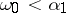. In this case

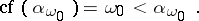A cardinal number 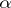is called a limit cardinal number if for any 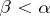there exists a 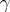such that 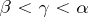. Examples of limit cardinal numbers are 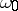and 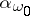, while 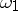is a non-limit cardinal number. A regular limit cardinal number is called weakly inaccessible. A cardinal number 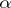is said to be a strong limit cardinal if for any 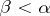, 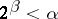. A strong regular limit cardinal number is called strongly inaccessible. It follows from the generalized continuum hypothesis that the classes of strongly- (or weakly-) inaccessible cardinal numbers coincide. The classes of inaccessible cardinal numbers can be further classified (the so-called Malo scheme), which leads to the definition of hyper-inaccessible cardinal numbers. The assertion that strongly- (or weakly-) inaccessible cardinal numbers exist happens to be independent of the usual axioms of axiomatic set theory.

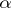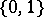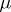A cardinal number is said to be measurable (more precisely, -measurable), if there exists a set of cardinality and a function defined on all elements of the set 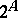, taking the values or and such that 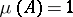, 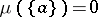for any 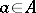and such that if 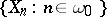is a sequence of pairwise disjoint subsets of 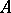, then

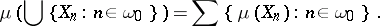Every cardinal number less than the first uncountable strongly-inaccessible cardinal number is non-measurable (Ulam's theorem), and the first measurable cardinal number is certainly strongly inaccessible. However, the first measurable cardinal number is considerably larger than the first uncountable strongly-inaccessible cardinal number (Tarski's theorem). It is not known (1987) whether the hypothesis that measurable cardinal numbers exist contradicts the axioms of set theory.

References

[1]	P.S. [P.S. Aleksandrov] Alexandroff, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian)
[2]	G. Cantor, , New ideas in mathematics , Handbook Math. Libraries , 6 (1914) pp. 90–184 (In Russian)
[3]	F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978))
[4]	K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968)
[5]	W. Sierpiński, "Cardinal and ordinal numbers" , PWN (1965) (Translated from Polish)

Comments

König's theorem stated above is usually called the König–Zermelo theorem.

References

[a1]	T.J. Jech, "Set theory" , Acad. Press (1978) pp. Chapt. 7 (Translated from German)
[a2]	A. Levy, "Basic set theory" , Springer (1979)