Difference between revisions of "Divisibility in rings"
(Importing text file) |
m (link) |
||
| Line 9: | Line 9: | ||
The last two properties are equivalent to saying that the set of elements divisible by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365016.png" /> forms an ideal, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365017.png" />, of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365018.png" /> (the principal ideal generated by the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365019.png" />), which contains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365020.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365021.png" /> is a ring with a unit element. | The last two properties are equivalent to saying that the set of elements divisible by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365016.png" /> forms an ideal, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365017.png" />, of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365018.png" /> (the principal ideal generated by the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365019.png" />), which contains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365020.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365021.png" /> is a ring with a unit element. | ||
| − | In an integral domain, elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365023.png" /> are simultaneously divisible by each other (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365024.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365025.png" />) if and only if they are associated, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365026.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365027.png" /> is an invertible element. Two associated elements generate the same principal ideal. The unit | + | In an integral domain, elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365023.png" /> are simultaneously divisible by each other (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365024.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365025.png" />) if and only if they are associated, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365026.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033650/d03365027.png" /> is an invertible element. Two associated elements generate the same principal ideal. The [[unit divisor]]s coincide, by definition, with invertible elements. A prime element in a ring is a non-zero element without proper divisors except unit divisors. In the ring of integers such elements are called primes (or prime numbers), and in a ring of polynomials they are known as irreducible polynomials. Rings in which — like in rings of integers or polynomials — there is unique decomposition into prime factors (up to unit divisors and the order of the sequence) are called factorial rings. For any finite set of elements in such a ring there exists a greatest common divisor and a lowest common multiple, both these quantities being uniquely determined up to unit divisors. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Kummer, "Zur Theorie der komplexen Zahlen" ''J. Reine Angew. Math.'' , '''35''' (1847) pp. 319–326</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> E. Kummer, "Zur Theorie der komplexen Zahlen" ''J. Reine Angew. Math.'' , '''35''' (1847) pp. 319–326</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966)</TD></TR> | ||
| + | </table> | ||
Revision as of 22:13, 30 November 2014
A generalization of the concept of divisibility of integers without remainder (cf. Division).
An element  of a ring
of a ring 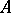 is divisible by another element
is divisible by another element 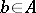 if there exists a
if there exists a 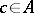 such that
such that 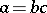 . One also says that
. One also says that 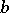 divides
divides  and
and  is said to be a multiple of
is said to be a multiple of  , while
, while 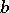 is the divisor of
is the divisor of  . The divisibility of
. The divisibility of  by
by 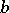 is denoted by the symbol
is denoted by the symbol 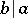 .
.
Any associative-commutative ring displays the following divisibility properties:
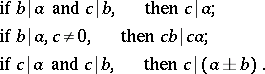 |
The last two properties are equivalent to saying that the set of elements divisible by  forms an ideal,
forms an ideal,  , of the ring
, of the ring 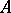 (the principal ideal generated by the element
(the principal ideal generated by the element 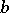 ), which contains
), which contains 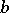 if
if 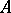 is a ring with a unit element.
is a ring with a unit element.
In an integral domain, elements  and
and 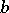 are simultaneously divisible by each other (
are simultaneously divisible by each other (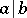 and
and 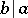 ) if and only if they are associated, i.e.
) if and only if they are associated, i.e. 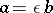 , where
, where  is an invertible element. Two associated elements generate the same principal ideal. The unit divisors coincide, by definition, with invertible elements. A prime element in a ring is a non-zero element without proper divisors except unit divisors. In the ring of integers such elements are called primes (or prime numbers), and in a ring of polynomials they are known as irreducible polynomials. Rings in which — like in rings of integers or polynomials — there is unique decomposition into prime factors (up to unit divisors and the order of the sequence) are called factorial rings. For any finite set of elements in such a ring there exists a greatest common divisor and a lowest common multiple, both these quantities being uniquely determined up to unit divisors.
is an invertible element. Two associated elements generate the same principal ideal. The unit divisors coincide, by definition, with invertible elements. A prime element in a ring is a non-zero element without proper divisors except unit divisors. In the ring of integers such elements are called primes (or prime numbers), and in a ring of polynomials they are known as irreducible polynomials. Rings in which — like in rings of integers or polynomials — there is unique decomposition into prime factors (up to unit divisors and the order of the sequence) are called factorial rings. For any finite set of elements in such a ring there exists a greatest common divisor and a lowest common multiple, both these quantities being uniquely determined up to unit divisors.
References
| [1] | E. Kummer, "Zur Theorie der komplexen Zahlen" J. Reine Angew. Math. , 35 (1847) pp. 319–326 |
| [2] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
| [3] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
Divisibility in rings. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Divisibility_in_rings&oldid=35233