Ockham algebra

A bounded distributive lattice together with a dual lattice endomorphism , i.e., a mapping such that the de Morgan laws and hold for all . The class of Ockham algebras is equational (i.e., is a variety; cf. also Algebraic systems, variety of). The Berman class is the subclass obtained by imposing on the dual endomorphism the restriction (, ). The Berman classes are related as follows:

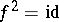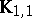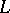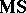The smallest Berman class is therefore the class described by the equation and is the class of de Morgan algebras. Perhaps the most important Berman class is , described by . This can be characterized as the class of Ockham algebras such that . It contains also the class of 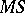-algebras , and, in particular, the class of 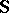of Stone algebras (add the relation ).

An Ockham algebra congruence is an equivalence relation that has the substitution property for both the lattice operations and the unary operation . A basic congruence is , defined by

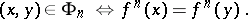If , then, for 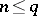, , where 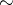indicates an isomorphism when is even and a dual isomorphism when is odd.

An Ockham algebra is subdirectly irreducible if it has a smallest non-trivial congruence. Every Berman class contains only finitely many subdirectly irreducible algebras, each of which is finite.

The class 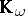of is given by

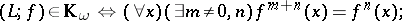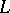it is a locally finite generalized variety that contains all of the Berman classes. If , then is subdirectly irreducible if and only if the lattice of congruences of 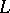reduces to the chain

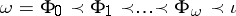where . If , then .

Ockham algebras can also be obtained by topological duality. Recall that a set in a partially ordered set 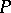is called a down-set if , , implies . Dually, is called an up-set if , , implies 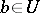. An ordered topological space (cf. also Order (on a set)) is said to be totally order-disconnected if, whenever 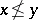, there exists a closed-and-open down-set such that and . A Priestley space is a compact totally order-disconnected space. An Ockham space is a Priestley space endowed with a continuous order-reversing mapping . The important connection with Ockham algebras was established by A. Urquhart and is as follows. If is an Ockham space and if denotes the family of closed-and-open down-sets of , then is an Ockham algebra, where is given by 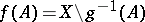. Conversely, if 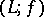is an Ockham algebra and if denotes the set of prime ideals of 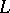, then, if 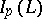is equipped with the topology which has as base the sets 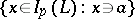and for every , is an Ockham space, where . Moreover, these constructions give a dual categorical equivalence. In the finite case the topology "evaporates" ; the dual space of a finite Ockham algebra 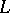consists of the ordered set 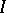of join-irreducible elements together with the order-reversing mapping .

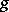Duality produces further classes of Ockham algebras. For , let be the subclass of formed by the algebras whose dual space satisfies . Then every Berman class is a 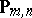; more precisely, . If is the dual space of 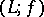, let, for every 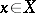, . If 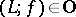is finite, then 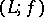is subdirectly irreducible if and only if there exists an such that . The dual space of a subdirectly irreducible Ockham algebra in can therefore be represented as follows (here the order is ignored and the arrows indicate the action of ):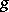

Figure: o110030a

The subdirectly irreducible Ockham algebra that corresponds to this discretely ordered space is denoted by . In particular, is the algebra whose dual space is

Figure: o110030b

and is described as follows:

Figure: o110030c

The subdirectly irreducible algebras in are the nineteen subalgebras of . Using a standard theorem of B.A. Davey from universal algebra, it is possible to describe completely the lattice of subvarieties of .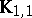

References

[a1]	T.S. Blyth, J.C. Varlet, "Ockham algebras" , Oxford Univ. Press (1994)
[a2]	J. Berman, "Distributive lattices with an additional unary operation" Aequationes Math. , 16 (1977) pp. 165–171
[a3]	H.A. Priestley, "Ordered sets and duality for distributive lattices" Ann. Discrete Math. , 23 (1984) pp. 39–60
[a4]	A. Urquhart, "Lattices with a dual homomorphic operation" Studia Logica , 38 (1979) pp. 201–209
[a5]	B.A. Davey, "On the lattice of subvarieties" Houston J. Math. , 5 (1979) pp. 183–192