Difference between revisions of "Chebotarev density theorem"
From Encyclopedia of Mathematics
(Importing text file) |
m (link) |
||
| Line 5: | Line 5: | ||
of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008011.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008012.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008013.png" /> integral. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008014.png" />, the norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008015.png" />, is the number of elements of the residue field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008016.png" />. This is the [[Frobenius automorphism|Frobenius automorphism]] (or Frobenius symbol) associated to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008017.png" />. | of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008011.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008012.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008013.png" /> integral. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008014.png" />, the norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008015.png" />, is the number of elements of the residue field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008016.png" />. This is the [[Frobenius automorphism|Frobenius automorphism]] (or Frobenius symbol) associated to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008017.png" />. | ||
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008018.png" /> is unramified in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008019.png" />, define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008020.png" /> as the conjugacy class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008021.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008022.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008023.png" /> is any prime ideal above <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008024.png" />. This conjugacy class depends only on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008025.png" />. | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008018.png" /> is unramified in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008019.png" />, define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008020.png" /> as the [[conjugacy class]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008021.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008022.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008023.png" /> is any prime ideal above <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008024.png" />. This conjugacy class depends only on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008025.png" />. |
The weak form of the Chebotarev density theorem says that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008026.png" /> is an arbitrary conjugacy class in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008027.png" />, then the set | The weak form of the Chebotarev density theorem says that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008026.png" /> is an arbitrary conjugacy class in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130080/c13008027.png" />, then the set | ||
Revision as of 20:57, 29 November 2014
Let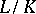 
be a normal (finite-degree) extension of algebraic number fields with Galois group 
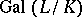. Pick a prime ideal 
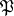of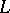 
and let 
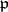be the prime ideal of 
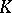under it, i.e. 
, where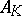 
is the ring of integers of 
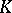. There is a unique element
 |
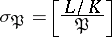of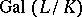 
such that 
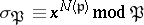for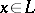 
integral. Here, 
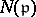, the norm of 
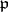, is the number of elements of the residue field 
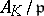. This is the Frobenius automorphism (or Frobenius symbol) associated to 
.
If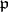 
is unramified in 
, define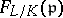 
as the conjugacy class of 
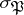in 
, where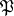 
is any prime ideal above 
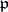. This conjugacy class depends only on 
.
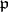The weak form of the Chebotarev density theorem says that if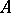 
is an arbitrary conjugacy class in 
, then the set
 |
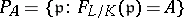is infinite and has Dirichlet density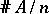 
, where 
.
The stonger form specifies in addition that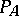 
is regular (see Dirichlet density) and that
 |
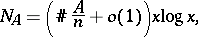with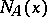 
the number of prime ideals in 
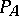with norm 
.
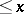References
| [a1] | W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , PWN/Springer (1990) pp. Sect. 7.3 (Edition: Second) |
| [a2] | N.G. Chebotarev, "Determination of the density of the set of primes corresponding to a given class of permutations" Izv. Akad. Nauk. , 17 (1923) pp. 205–230; 231–250 (In Russian) |
| [a3] | N.G. Chebotarev, "Die Bestimmung der Dichtigkeit einer Menge von Primzahlen welche zu einer gegebenen Substitutionsklasse gehören" Math. Ann. , 95 (1926) pp. 191–228 |
How to Cite This Entry:
Chebotarev density theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebotarev_density_theorem&oldid=35122
Chebotarev density theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebotarev_density_theorem&oldid=35122
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article