Difference between revisions of "Fractions, ring of"
(Importing text file) |
(→Comments: See Field of fractions) |
||
| Line 13: | Line 13: | ||
====Comments==== | ====Comments==== | ||
| − | This notion is also called a ring of quotients. | + | This notion is also called a ring of quotients. For a commutative [[integral domain]] we obtain the [[field of fractions]]. |
Revision as of 21:26, 28 November 2014
A ring related to a given associative ring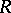 
with an identity. The (right classical) ring of fractions of 
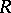is the ring 
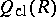in which every regular element (that is, not a zero divisor) of 
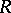is invertible, and every element of 
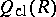has the form 
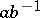with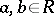 
. The ring 
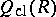exists if and only if 
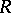satisfies the right-hand Ore condition (cf. Associative rings and algebras). The maximal (or complete) right ring of fractions of 
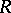is the ring 
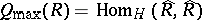, where 
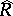is the injective hull of 
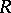as a right 
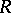-module, and 
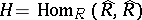is the endomorphism ring of the right 
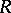-module 
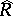. The ring 
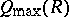can also be defined as the direct limit
 |
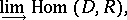where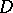 
is the set of all dense right ideals of 
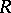(a right ideal 
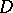of a ring 
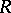is called a dense ideal if
 |
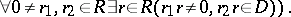References
| [1] | J. Lambek, "Lectures on rings and modules" , Blaisdell (1966) |
| [2] | V.P. Elizarov, "Quotient rings" Algebra and Logic , 8 : 4 (1969) pp. 219–243 Algebra i Logika , 8 : 4 (1969) pp. 381–424 |
| [3] | B. Stenström, "Rings of quotients" , Springer (1975) |
Comments
This notion is also called a ring of quotients. For a commutative integral domain we obtain the field of fractions.
Fractions, ring of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractions,_ring_of&oldid=35066